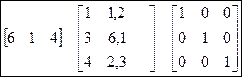Умножение матрицы на скаляр.

Чтобы умножить матрицу на скаляр, нужно умножить на скаляр каждый элемент матрицы.

1. Введем в ячейки электронной таблицы скаляр, представляющий собой константу и матрицу B4:C6, которую нужно умножить на него.

2. В ячейку B9 введем формулу =$B$3*B4.

3. Копируем формулы из ячейки B9 в диапазон B9:C11.

4. Результат отображается в ячейках B9:С11.

Рис. 8 Умножение матрицы на скаляр.

Перемножение матриц.

Две матрицы можно перемножить при условии, что количество столбцов первой матрицы равно количеству строк второй матрицы. («Внутренние» размеры матрицы должны совпадать, размеры результирующей матрицы состоят из «внешних» размеров).

1. Ввести матрицу 3х2 (произвольные числа) в ячейки A4:B6.

2. В ячейки A9:A10 ввести матрицу 2х1 (произвольные числа).

3. Выделить ячейки C4:C6.

4. В строке функций набрать формулу =МУМНОЖ(A4:B6;A9:A10).

5. Нажать сочетание клавиш CTRL+SHIFT+ENTER.

Рис. 9 Умножение матриц.

Транспонирование матриц.

Чтобы транспонировать любую матрицу, нужно поменять ее строки и столбцы. В Excel это можно сделать двумя способами. Рассмотрим оба метода.

С помощью команды меню «Специальная вставка»

1. Введите исходную матрицу.

2. Выделите ячейки, в которых содержатся эта матрица.

3. Скопируйте их содержимое в буфер обмена.

4. Установите указатель мыши на ячейку, в которой будет содержаться верхнее левое значение транспонированной матрицы.

5. Дайте команду Правка > Специальная вставка.

6. Отобразится диалоговое окно Специальная вставка.

 

Рис. 10 Окно «Специальная вставка»

7. На панели Вставить установите переключатель в положение значение и установите флажок транспонировать, расположенный в нижней части диалогового окна.

8. Нажмите OK.

С помощью функции массива.

1. Введите исходную матрицу.

2. Укажите, куда нужно поместить результат (выделите диапазон ячеек).

3. В окне формул введите функцию =ТРАНСП(матрица).

4. Укажите с помощью мышки диапазон, в котором содержится матрица.

5. Завершите функцию нажатием клавиш CTRL+SHIFT+ENTER.

Задание.

Транспонируйте обоими способами приведенные ниже матрицы.

Обращение матриц.

Операция обращения матриц применима только к квадратным матрицам. Однако не для каждой матрицы существует обратная к ней матрица. Чтобы матрицу можно было обратить, она должна быть несингулярной. (детерминант матрицы должен быть отличен от 0).

Детерминант матрицы – это скалярная величина, которая вычисляется на основе всех матричных элементов и часто используется при решении систем уравнений.

Для вычисления детерминанта в Excel используется функция массива =МОПРЕД(матрица). Если он отличен от 0, то матрицу можно обратить.

1 Введите матрицу, которую нужно обратить.

2 Вычислите ее детерминант. Если он не равен 0 – продолжите процесс обращения, иначе измените исходные данные.

3 Укажите место для размещения обратной матрицы и ее правильный размер - он совпадает с размером исходной матрицы.

4 Начните вводить функцию массива =МОБР(матрица) и укажите с помощью мыши ячейки, в которых содержится обращаемая матрица.

5 Нажмите сочетание клавиш CTRL+SHIFT+ENTER.