
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент інерції твердого тіла. Мотенти інерції тіл найпростішої форми.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Момент інерції - скалярна фізична величина, міра інертності при обертальному русі навколо осі, подібно до того, як маса тіла є мірою його інертності в поступальному русі. Характеризується розподілом мас у тілі: дорівнює сумі добутків мас частинок тіла на квадрати їхніх відстаней від осі обертання.
Момент інерції твердого тіла відносно якої-небудь осі залежить не тільки від маси, форми і розмірів тіла, але також від положення тіла по відношенню до цієї осі. Згідно теоремі Штейнера (теоремі Гюйгенса-Штейнера), момент інерції тіла J щодо довільної осі дорівнює сумі моменту інерції цього тіла J c щодо осі, що проходить через центр мас тіла паралельно розглядається осі, і твори маси тіла m на квадрат відстані d між осями:
Якщо
де Наприклад, момент інерції стрижня відносно осі, що проходить через його кінець, дорівнює:
Теорема Штейнера Теорема Штейнера: момент інерції тіла відносно довільної осі дорівнює сумі моменту інерції
16) Рівняння обертального руху ТТ
Основне рівняння динаміки обертального руху За другим законом Ньютона можна сформулювати рівняння обертального руху, де зовнішнім силам, які діють на тіло, відповідають моменти сил, масі — момент інерції, а прискоренню — кутове прискорення. При одновісному обертанні
Тут Mi — моменти зовнішніх сил,
17) Моме́нт си́ли — векторна фізична величина, рівна векторному добутку радіус-вектора, проведеного від осі обертання до точки прикладення сили, на вектор цієї сили. Момент сили є мірою зусилля, направленого на обертання тіла. Момент сили зазвичай позначається латинською літерою
Момент сили
тобто є векторним добутком радіус-вектора Момент сили - це вектор перпендикулярний, як до радіус-вектора точки, так і до сили, яка на цю точку діє. За абсолютною величиною момент сили дорівнює добутку сили на плече
де α - кут між напрямком сили й радіус-вектором точки. Плече сили відносно точки (у механіці) - найкоротша відстань від даної точки до лінії дії сили, тобто довжина перпендикуляра, опущеного з цієї точки на лінію дії сили. Новак Правило важелів Архімеда Правило важелів Архімеда: нерівні тягарі перебувають у рівновазі на важелі, якщо відстані центрів тягарів від точки опори важеля обернено пропорційні їх вагам. 19. Дисипативна енергія Дисипація енергії - зменшення механічної енергіє системи в процесі руху. Дисипати́вна систе́ма (або дисипати́вна структу́ра) — відкрита нелінійна система, яка є далекою від стану термодинамічної рівноваги. Така система є нерівноважною завдяки розсіянню енергії, одержуваної ззовні. Внаслідок самоорганізації у таких системах можуть виникати стійкі структури, які існують за умови постійної дисипації, тобто втрати системою енергії. З появою складної впорядкованої структури в системі зростає ентропія, яка компенсується негативним потоком ентропії зовні. Дисипативна структура здійснює постійний обмін речовиною та енергією із середовищем, в котрому вона народилася, та є структурно стійкою у ньому. Класичним прикладом таких структур є комірки Бенара, винайдені у 1900 році. Ці комірки утворюються у воді, котру постійно підігрівають знизу, за рахунок конвекційних потоків. Як тільки система переходить в рівноважний стан, тобто підігрівання води припиняють, ці структури зникають.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.242.223 (0.008 с.) |


 відносно геометричної осі
відносно геометричної осі

 відносно геометричної осі
відносно геометричної осі
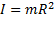



 відносно осі, перпендикулярної до середини стержня
відносно осі, перпендикулярної до середини стержня



 - Момент інерції тіла відносно осі, що проходить через центр мас тіла, то момент інерції щодо паралельної осі, розташованої на відстані
- Момент інерції тіла відносно осі, що проходить через центр мас тіла, то момент інерції щодо паралельної осі, розташованої на відстані  від неї, дорівнює
від неї, дорівнює ,
, - Повна маса тіла.
- Повна маса тіла.
 відносно осі, яка паралельна даній, і добутку маси
відносно осі, яка паралельна даній, і добутку маси 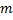 тіла на квадрат відстані
тіла на квадрат відстані  між осями:
між осями:

 — кутова швидкість,
— кутова швидкість,  — кутове прискорення.
— кутове прискорення. і вимірюється в системі СІ в Н*м
і вимірюється в системі СІ в Н*м , яка діє на матеріальну точку із радіус-вектором
, яка діє на матеріальну точку із радіус-вектором  визначаєтся як
визначаєтся як .
. ,
,


