
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 1.1 (переводим целые числа из десятичной системы счисления в систему счисления с основанием P и наоборот)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление Оглавление 1 1. Системы счисления 4 Лабораторная работа 1.1 (переводим целые числа из десятичной системы счисления в систему счисления с основанием P и наоборот) 4 Лабораторная работа 1.2 (переводим целые числа из системы счисления с основанием P в систему счисления с основанием Q=PK и наоборот без промежуточного перевода в десятичную систему) 4 Лабораторная работа 1.3 (складываем целые числа в системе счисления с основанием P без перевода в десятичную) 5 Лабораторная работа 1.4 (простые и не очень простые вопросы и задачи по системам счисления) 6 2. Операторы ввода и форматного вывода 7 Лабораторная работа 2.1 (учимся вводить данные с клавиатуры, вычислять большие формулы и выводить результат на экран) 7 3. Операторы ввода, вывода и присваивания 8 Лабораторная работа 3.1 (первые простые содержательные задачи) 8 Лабораторная работа 3. 2(осваиваем оператор присваивания) 9 4. Условный оператор 10 Лабораторная работа 4.1 (учим компьютер спрашивать) 10 5. Оператор множественного выбора 12 Лабораторная работа 5.1 (на один вопрос – много ответов; что же выбрать?) 12 6. Логические переменные и операции 13 Лабораторная работа 6.1 (таблица истинности) 13 Лабораторная работа 6.2 (бросаем точку на плоскость и наблюдаем за ней) 14 Лабораторная работа 6.3 (составляем логические условия) 16 7. Операторы цикла 17 Лабораторная работа 7.1 (вычисляем суммы и произведения конечных рядов) 17 Лабораторная работа 7.2 (оператор цикла с предусловием – исследуем числа) 17 Лабораторная работа 7.3 (еще раз тренируемся в использовании оператора цикла) 18 Лабораторная работа 7.4 (факториал, Фибоначчи, Евклид и...) 20 Лабораторная работа 7.5 (обрабатываем последовательности) 21 Лабораторная работа 7.6 (препарируем целые числа) 22 Лабораторная работа 7.7 (опять целые числа, но мастерство – на ступень выше) 23 8. Символьные данные 24 Лабораторная работа 8.1 (узнаем у компьютера, какими он пользуется символами) 24 Лабораторная работа 8.2 (впервые обрабатываем не числа, а текст) 24 9. Подпрограммы (процедуры и функции) 25 Лабораторная работа 9.1 (задачи знакомые, но записываем их в новой форме) 25 10. Численные методы 27 Лабораторная работа 10.1 (приближенно решаем уравнения) 27 Лабораторная работа 10.2 (приближенно находим площади криволинейных фигур) 28
11. Одномерные массивы 29 Лабораторная работа 11.1 (наконец-то – от простых переменных переходим к массивам) 29 Лабораторная работа 11.2 (те же массивы, но задачи посложнее) 30 12. Двумерные массивы 31 Лабораторная работа 12.1 (крестики-нолики, морской бой, шахматы, … – без двумерных массивов не обойтись) 31 Лабораторная работа 12.2 (гуляем по матрице прямо и зигзагами) 33 13. Графика 34 Лабораторная работа 13.1 (на первых подступах к красоте) 34 Лабораторная работа 13.2 (графики функций в декартовой системе координат – помощь по математике) 35 Лабораторная работа 13.3 (графики кривых в полярной системе координат – и математика и красота одновременно) 36 Лабораторная работа 13.4 (не только рисуем, но и двигаем картинку по экрану) 36 Лабораторная работа 13.5 (довольно сложные, но интересные задачи по графике) 37 Лабораторная работа 13.6 (математические задачи с графическими иллюстрациями) 38 14. Строки 39 Лабораторная работа 14.1 (работаем уже не с отдельными символами, а с целой строкой) 39 Лабораторная работа 14.2 (учимся разбивать строку на слова) 40 15. Множества 42 Лабораторная работа 15.1 (очень легкий материал – передышка после процедур, функций, массивов, …) 42 16. Записи 43 Лабораторная работа 16.1 (оказывается, переменная может состоять из полей совершенно разного типа). 43 16. Файлы 44 Лабораторная работа 16.1 (приступаем к изучению типизированных файлов) 44 Лабораторная работа 16.2 (используем все наши знания и пишем собственную базу данных) 45 Лабораторная работа 16.3 (текстовые файлы – незаменимый инструмент для отладки программ с большим количеством исходных данных) 47 18. Динамическая память (первый шаг к современному программированию) 48 Лабораторная работа 18.1 (линейные однонаправленные списки – не так трудно, как кажется) 48 19. Краткий справочник 51 20. Литература. 54
Системы счисления Условный оператор Операторы цикла Лабораторная работа 6.1 (вычисляем суммы и произведения конечных рядов)
Вводятся действительные a и x и натуральное n. Вычислить Y:
1. Y= sin (x) + sin(x2) + … + sin(xn). 2. Y= cos(x) + cos(2x) + … + cos(nx). 3. Y= x + x/2 + x/3 + … + x/n. 4. Y= x + x2 + x3 + … + xn. 5. Y= x + x2/2 + x3/3 + … +xn/n. 6. Y= x + x3/3 + x5/5 + … + x2n-1/(2n-1). 7. Y= a + x2/2 + x4/4 + … + x2n/2n. 8. Y= nxn-1 + (n-1)xn-2 + … + 2x + 1.
9. Y= x + (1+2)x2 + (1+2+3)x3 + … +(1+2+3+…+n)xn. 10. Y= 1! + 2! + … + n!. 11. Y= (1+sin(0.1)) (2+sin(0.2)) … (n+sin(n/10)). 12. Y= x(x+1) (x+2) … (x+n-1). 13. Y= 1/sin(1) + 2/(sin(1)+sin(2)) + … +n/(sin(1)+sin(2)+…+sin(n)). 14. Y= x - x2 + x3 – x4 + … + (-1)xn. 15. Y= -x + x2 - x3 + … + (-1)xn. 16. Y= nx + (n-1)x2 + (n-2)x3 +… + xn.
Лабораторная работа 6.2 (оператор цикла с предусловием – исследуем числа)
Вводится последовательность положительных целых чисел, за которой следует 0 (признак конца последовательности). Определить сумму чисел, их количество, минимальное и максимальное число с их порядковыми номерами среди тех введенных чисел, которые обладают следующими свойствами:
1. находятся между 11 и 99; 2. имеют четный порядковый номер ввода; 3. кратны пяти; 4. оканчиваются на цифру нуль; 5. имеют нечетный порядковый номер ввода; 6. четные; 7. оканчиваются на цифру семь; 8. нечетные; 9. оканчиваются на цифру один; 10. оканчиваются на цифру три; 11. кратны семи; 12. кратны трем; 13. оканчиваются на цифру пять; 14. однозначные; 15. двузначные; 16. трехзначные;
Лабораторная работа 6.3 (еще раз тренируемся в использовании оператора цикла)
1. Даны натуральные числа x и y. Найти произведение x*y, используя лишь операцию сложения. Задачу решить двумя способами (первый способ – x*y, второй – y*x). 2. Составить программу возведения натурального числа в квадрат, учитывая следующую закономерность: 3. Найти сумму 12+22+32+…+102. Учесть особенности получения квадрата натурального числа, отмеченные в предыдущей задаче. 4. Составить программу возведения натурального числа в третью степень, учитывая следующую закономерность: 5. Одноклеточная амеба каждые три часа делится на две клетки. Определить, сколько клеток будет через 3, 6, 9, …, 24 часа, если первоначально была одна амеба. 6. Ученик A открыл первого сентября счет в банке, вложив X рублей. Каждый месяц размер вклада увеличивается на 2% от текущей суммы. Какой суммой денег будет располагать ученик к концу июня, чтобы отпраздновать успешное окончание учебного года? 7. Вводится натуральное число N. Вычислить: 8. На полу около стенки наклонно стоит палка длиной L метров. Нижний конец находится на расстоянии X метров от стенки. Палка начинает скользить и падает на пол. Определить значение угла между палкой и полом (в градусах) с момента начала скольжения до падения палки через каждые 0.1 метра. 9. В сентябре поступивший в школу №1580 ученик идет от дома до школы прогулочным шагом со скоростью 3 км/час и тратит на это путешествие t часов времени. Но количество задаваемых на дом работ увеличивается каждый месяц на 3% по отношению к предыдущему месяцу, и в таком же соотношении увеличивается скорость ученика. Спрашивается, с какой скоростью и за какое время он будет пробегать этот же путь в конце мая. 10. Определить суммарный объем в литрах 12 вложенных друг в друга шаров со стенками толщиной 5 мм. Внутренний диаметр внутреннего шара равен 10 см. Принять, что шары вкладываются друг в друга без зазоров. 11. В некоторой стране используются купюры следующего достоинства 1, 2, 4, 8, 16, 32 и 64 единиц. Как наименьшим количеством купюр можно расплатиться за товар стоимостью в N единиц (указать количество каждой из купюр). Считаем, что имеется достаточное количество купюр всех достоинств. 12. Начав тренировки, лыжник в первый день пробежал 10 км. Каждый следующий день он увеличивал длину пробега на 10% от пробега предыдущего дня. Определить:
13. Вводится действительное число A.
Лабораторная работа 6.4 (факториал, Фибоначчи, Евклид и...)
1. Вводится натуральное число. Определить, является ли оно простым. 2. Вводится натуральное число n. Вычислить его факториал (n!). 3. Вводятся натуральные n и k. Вычислить nk. 4. Вводится радиус круга R. Подсчитать, сколько точек с целочисленными координатами попадают в круг радиуса R с центром в начале координат. 5. Вводится натуральное n. Получить наименьшее число вида 2R, превосходящее n. 6. Вводится натуральное число n. Определить, является ли оно совершенным. Например 6 – совершенное число, т.к. 6=1+2+3. 7. Вычислить наименьшее общее кратное двух чисел, используя алгоритм Евклида для вычисления их наибольшего общего делителя. 8. Даны натуральные числа a и b, являющиеся соответственно числителем и знаменателем дроби. Сократить дробь, найдя наибольший общий делитель (НОД(a,b)) по алгоритму Евклида. 9. Даны натуральные числа a и b (a>b). Найти результат и остаток целочисленного деления a на b, не используя стандартных операций DIV и MOD. 10. Вводится натуральное число n. Найти n-ое число Фибоначчи. 11. Вводится натуральное число n. Найти сумму первых n чисел Фибоначчи. 12. Задан прямоугольник размером A*B (A и B- натуральные). От прямоугольника каждый раз отрезаются квадраты максимальной площади. Найти общее количество квадратов. 13. Вводятся три натуральных числа a, b и c. Найти их наибольший общий делитель по алгоритму Евклида, учитывая, что НОД(a,b,c)=НОД(НОД(a,b),c). 14. Вводятся два натуральных числа. Найти их наибольший общий делитель по алгоритму Евклида. 15. Вводится факториал некоторого числа N. Найти число N.
Символьные данные Лабораторная работа 7.1 (узнаем у компьютера, какими он пользуется символами)
Вывести на экран таблицу символов с соответствующими кодами.
Численные методы Одномерные массивы Двумерные массивы Лабораторная работа 11.1 (крестики-нолики, морской бой, шахматы, … – без двумерных массивов не обойтись)
1. Дана прямоугольная матрица целых чисел. Найти максимальный элемент матрицы с указанием номеров строки и столбца, на пересечении которых он находится. 2. Дана прямоугольная матрица целых чисел. Выписать максимальный элемент в каждой строке, указав его номер столбца.
3. Дана прямоугольная матрица целых чисел. Выписать максимальный элемент в каждом столбце, указав его номер строки. 4. Дана прямоугольная матрица целых чисел. Найти сумму элементов каждой строки. 5. Дана прямоугольная матрица целых чисел. Найти сумму элементов каждого столбца. 6. Дана квадратная матрица целых чисел. Поменять местами элементы главной и побочной диагоналей. 7. Дана квадратная матрица целых чисел. Выписать все элементы матрицы, находящиеся выше главной диагонали. 8. Дана квадратная матрица целых чисел. Выписать все элементы матрицы, находящиеся ниже главной диагонали. 9. Дана квадратная матрица целых чисел. Выписать все элементы матрицы, находящиеся выше побочной диагонали. 10. Дана квадратная матрица целых чисел. Выписать все элементы матрицы, находящиеся ниже побочной диагонали. 11. Дана квадратная матрица целых чисел. Поменять местами элементы матрицы симметрично главной диагонали. 12. Дана квадратная матрица целых чисел. Найти максимум среди элементов главной диагонали, указав номера строки и столбца, на пересечении которых он находится. 13. Дана квадратная матрица целых чисел. Найти максимум среди элементов побочной диагонали, указав номера строки и столбца, на пересечении которых он находится. 14. Дана квадратная матрица целых чисел. Выписать все элементы матрицы, находящиеся в ее верхней половине между главной и побочной диагоналями. 15. Дана квадратная матрица целых чисел. Выписать все элементы матрицы, находящиеся в ее нижней половине между побочной и главной диагоналями. 16. Дана квадратная матрица целых чисел. Выписать все элементы матрицы, находящиеся в ее левой половине между главной и побочной диагоналями. 17. Дана квадратная матрица целых чисел. Выписать все элементы матрицы, находящиеся в ее правой половине между побочной и главной диагоналями. 18. Назовем седловой точкой матрицы элемент минимальный в строке и максимальный в столбце, или максимальный в строке и минимальный в столбце. Найти все седловые точки прямоугольной матрицы целых чисел. 19. Дана матрица, элементами которой являются вещественные числа. Создать одномерный массив, элементами которого являются суммы отрицательных элементов столбцов данной матрицы. 20. Дана матрица, элементами которой являются вещественные числа. Создать одномерный массив, элементами которого являются суммы положительных элементов строк данной матрицы. 21. Дана матрица N*M, элементами которой являются целые числа и номер столбца K. Сдвинуть все столбцы с K-ого по M-ый на один влево. 22. Дана матрица N*M, элементами которой являются целые числа и номер строки K. Сдвинуть все строки с K-ой по N-ую на одну вверх.
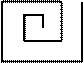
Лабораторная работа 11.2 (гуляем по матрице прямо и зигзагами)
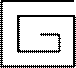
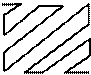
Заполнить матрицу размером 5*5 целыми числами от 1 до 25 по схеме.
Графика Строки Множества Лабораторная работа 14.1 (очень легкий материал – передышка после процедур, функций, массивов, …)
1. Дана строка из строчных латинских букв. Напечатать первые вхождения букв в текст, сохраняя их исходный взаимный порядок. 2. Дана строка из строчных латинских букв. Напечатать в алфавитном порядке все буквы, входящие в текст не менее двух раз. 3. Дана строка из строчных латинских букв. Напечатать в алфавитном порядке все буквы, входящие в текст по одному разу. 4. Вводится натуральное число. Подсчитать количество различных цифр в его записи. 5. Вводится натуральное число. Выписать в возрастающем порядке все цифры, не входящие в запись данного числа. 6. Дано натуральное число N. Используя метод «решета Эратосфена» выписать все простые числа от 1 до N в убывающем порядке. 7. Дан массив из N натуральных чисел. Выписать в возрастающем порядке те цифры, которые не входят ни в одно из этих чисел. 8. Дан массив из N натуральных чисел. Выписать в возрастающем порядке те цифры, которые входят во все эти числа. 9. Задать два множества A и B (одного и того же типа). Поменять местами значения A и B, не используя дополнительных переменных. 10. Дан массив из N натуральных чисел. Выписать в убывающем порядке те цифры, которые не входят ни в одно из четных. 11. Дан массив из N натуральных чисел. Выписать в убывающем порядке те цифры, которые входят во все нечетные числа.
В заданиях с 12-го по 15-ое вводится строка - последовательность слов из строчных русских букв, между соседними словами - запятая, за последним словом - точка. Напечатать в алфавитном порядке: 12. Все гласные буквы, которые входят в каждое слово. 13. Все согласные буквы, которые не входят ни в одно слово. 14. Все звонкие согласные буквы, которые входят хотя бы в одно слово. 15. Все звонкие согласные буквы, которые входят в каждое нечётное слово. Примечание: гласные буквы: а, е, и, о, у, ы, э, ю, я; согласные буквы: все остальные буквы, кроме ь, ъ; звонкие согласные: б, в, г, д, ж, з, л, м, н, р.
Записи Лабораторная работа 15.1 (оказывается, переменная может состоять из полей совершенно разного типа).
1. Задано время T. Определить, чему будет равно время спустя одну секунду (с учетом смены минут, часов и суток). 2. Написать программу, вычисляющую время, прошедшее от времени T1 до времени T2, считая, что T2>T1. 3. Написать программу для проверки предшествует ли время T1 времени T2 (в рамках суток). 4. Заданы два поля шахматной доски. Определить, может ли ферзь за один ход перейти с первого поля доски на второе поле. 5. При задаваемых датах рождения определить, кто старше из двух друзей. 6. На столе выложены в ряд костяшки домино. Проверить, составляют ли они правильную последовательность. 7. Заданы две окружности. Определить их взаимное расположение (пересекаются, одна в другой, удалены друг от друга). В заданиях с 8-го по 16-ое задан набор из N кубиков (N указано в константе). Каждый кубик характеризуется следующими параметрами: размер ребра, вес, цвет. 8. Отсортировать кубики по размеру. 9. Отсортировать кубики по цвету. 10. Отсортировать кубики по весу. 11. Вывести на экран порядковый номер и параметры самого тяжелого кубика. 12. Вывести на экран порядковый номер и параметры самого маленького кубика. 13. Отсортировать кубики по цветам, а внутри одного цвета – по размеру. 14. Отсортировать кубики по размеру, а внутри одного размера – по весу. 15. Отсортировать кубики по цветам, внутри одного цвета – по размеру, а внутри одного размера – по весу. 16. Вывести на экран порядковые номера и параметры всех кубиков цвета Color (Color вводится) и суммарный вес этих кубиков. 17. Подсчитать количество самых крупных кубиков и вывести на экран их порядковые номера и параметры.
Файлы Лабораторная работа 16.1 (приступаем к изучению типизированных файлов)
1. Вводится файл натуральных чисел (file of integer). Требуется найти среднее арифметическое этих чисел и создать еще один файл, переписав в него все числа из первого файла, большие среднего арифметического. 2. Вводится файл целых чисел (file of integer). Требуется отсортировать числа в файле по возрастанию. Дополнительный файл не использовать. 3. Вводится файл целых чисел (file of integer). Создать еще один файл и переписать в него все положительные числа из первого файла, удалив их оттуда. 4. Вводится файл символов (file of char). Упорядочить файл по алфавиту. 5. Вводятся два упорядоченных по возрастанию файла целых чисел. Объединить их в третий файл, также упорядоченный по возрастанию. 6. Вводятся два файла целых чисел. Первый файл упорядочен по возрастанию, а второй – по убыванию. Объединить их в третий файл, упорядоченный по возрастанию. 7. Вводится файл строк (file of string). Создать файл целых чисел и записать в каждую строку этого файла, сколько повторяющихся маленьких латинских букв находится в соответствующей строке первого файла. 8. Вводится файл целых чисел в следующем порядке: четыре положительных, четыре отрицательных, четыре положительных, четыре отрицательных и т.д. (нулевых компонент в файле нет). Переписать эти данные в другой файл, но уже в таком порядке: два положительных, два отрицательных, два положительных, два отрицательных и т.д. 9. Даны два файла целых чисел (file of integer), содержащие коэффициенты двух полиномов, начиная со старших степеней. Перемножить два полинома и результат (коэффициенты третьего полинома) поместить в третий файл того же типа. 10. Даны два файла целых чисел (file of integer), содержащие коэффициенты двух многочленов, начиная со старших степеней. Сложить два многочлена и результат (коэффициенты третьего многочлена) поместить в третий файл того же типа. 11. Вводится файл целых чисел (file of integer). Создать еще один файл и переписать в него все четные числа, удалив их из первого файла. 12. Даны два файла целых чисел (file of integer), содержащие коэффициенты двух многочленов, начиная со старших степеней. Вычесть из первого многочлена второй и результат (коэффициенты третьего многочлена) поместить в третий файл того же типа. 13. Вводится файл строк (file of string). Создать файл целых чисел и записать в каждую строку этого файла числовое значение суммы цифр, находящихся в соответствующей строке первого файла. 14. Вводится файл целых чисел (file of integer). Если число компонент файла чётное, вставить число 100 в середину файла. Дополнительный файл не использовать. 15. Вводится файл целых чисел (file of integer).Найти минимальный компонент файла (их может быть несколько) и после каждого вставить 0. Дополнительный файл не использовать.
Краткий справочник
Герона формула. Герон – выдающийся греческий инженер и математик, живший в г.Александрия в первом веке до н.э. Дал систематическое изложение основных достижений древности в области прикладной механики. Математические работы Герона являются энциклопедией античной прикладной математики. Формула Герона позволяет вычислить площадь треугольника по трем его сторонам: P = Ö (P*(P-a)*(P-b)*(P-c)), где: a, b и c – стороны треугольника, P – полупериметр (P=(a+b+c)/2).
Евклида алгоритм. Евклид –древнегреческий математик, живший в г.Александрия в третьем веке до н.э. Важнейший труд Евклида «Начала», содержащий изложение планиметрии, стереометрии и некоторых вопросов теории чисел, оказал огромное влияние на развитие математики. Алгоритм Евклида нахождения наибольшего общего делителя (НОД) неотрицательных целых чисел основан на следующих свойствах этой величины. Пусть m и n – одновременно не равные нулю целые неотрицательные числа и пусть.m³n Тогда, если n=0, то НОД(m,n)=m, а если n¹0, то для чисел m, n и r, где r – остаток от деления m на n, выполняется равенство НОД(m,n)=НОД(n,r). Например, НОД(15,6)=НОД(6,3)=НОД(3,0)=3. Натуральное число. Числа 1, 2, 3 и т.д., использующиеся для счета предметов, т.е. целые положительные числа, называются натуральными.
Палиндром. Палиндром – это число, которое читается одинаково справа налево и слева направо. Например, числа 1221, 343, 66 – палиндромы. Понятие палиндром применимо и к тексту. Например, слово «шалаш» это тоже палиндром.
Прогрессия арифметическая. Последовательность, каждый член которой, начиная со второго, получен сложением предыдущего члена с некоторым постоянным числом D, называется арифметической прогрессией. Число D – разность прогрессии.
Прогрессия геометрическая. Последовательность, первый член которой отличен от нуля и каждый член, начиная со второго, получен умножением предыдущего члена на некоторое постоянное число Q ¹ 0, называется геометрической прогрессией. Число Q – знаменатель прогрессии.
Простое число. Простым называется число, которое делится только на единицу и на само себя.
Совершенное число. Совершенным называется число, которое равно сумме своих делителей (конечно, за исключением себя самого). Например, число 6 – совершенное, т.к. 6 = 1 + 2 + 3.
Среднее арифметическое. Среднее арифметическое чисел a1, a2, a3, …,an это сумма этих чисел, деленная на их количество (n).
Среднее геометрическое. Среднее геометрическое чисел a1, a2, a3, …,an – это корень n–ой степени из произведения этих чисел. Факториал. Факториалом натурального числа n называется произведение натуральных чисел от 1 до n. Обозначается n!. Фибоначчи числа. Фибоначчи Леонардо – итальянский математик из г.Пиза (иначе его звали Леонардо Пизанский), живший в XII-XIII веке. Путешествуя по Востоку, Леонардо познакомился с достижениями арабской математики, и его труды способствовали передаче этих знаний на Запад. Фибоначчи описал интересную последовательность чисел: первые два числа равны единице, а каждое следующее равно сумме двух предыдущих (1, 1, 2, 3, 5, 8, 13, …).
Эратосфена решето. Эратосфен жил в третьем веке до н.э.; родился он в Африке, учился в Александрии и Афинах. Эратосфен был очень разносторонним человеком: он занимался наукой (астрономией, географией, математикой), а также филологией, музыкой и поэзией. Эратосфен предложил алгоритм, с помощью которого можно определить все простые числа в заданном диапазоне. Суть алгоритма в следующем: выписываются все натуральные числа от 2 до границы заданного диапазона; выбирается первое из них (это 2, простое число) и вычеркиваются все кратные ему числа, кроме него самого; затем берется следующее из невычеркнутых чисел (это 3, также простое число) и опять вычеркиваются кратные ему числа и т. д. В конце концов, останутся только простые числа, начиная с 2.
Литература. 1. С.А.Абрамов, Г.Г.Гнездилова, Е.Н.Капустина, М.И.Селюн Задачи по программированию. – М.: «Наука», 1988. 2. В.Н.Пильщиков Сборник упражнений по языку Паскаль. – М.: «Наука», 1989. 3. Е.Андреева, И.Фалина Системы счисления и компьютерная арифметика. – М.: «Лаборатория базовых знаний», 2000 4. О.П.Зеленяк Практикум по программированию на TUBO PASCAL.- Киев: «ДиаСофт», 2001 5. Д.М.Златопольский Я иду на урок информатики. – М.: «Первое сентября», 2001 Оглавление Оглавление 1 1. Системы счисления 4 Лабораторная работа 1.1 (переводим целые числа из десятичной системы счисления в систему счисления с основанием P и наоборот) 4 Лабораторная работа 1.2 (переводим целые числа из системы счисления с основанием P в систему счисления с основанием Q=PK и наоборот без промежуточного перевода в десятичную систему) 4 Лабораторная работа 1.3 (складываем целые числа в системе счисления с основанием P без перевода в десятичную) 5 Лабораторная работа 1.4 (простые и не очень простые вопросы и задачи по системам счисления) 6 2. Операторы ввода и форматного вывода 7 Лабораторная работа 2.1 (учимся вводить данные с клавиатуры, вычислять большие формулы и выводить результат на экран) 7 3. Операторы ввода, вывода и присваивания 8 Лабораторная работа 3.1 (первые простые содержательные задачи) 8 Лабораторная работа 3. 2(осваиваем оператор присваивания) 9 4. Условный оператор 10 Лабораторная работа 4.1 (учим компьютер спрашивать) 10 5. Оператор множественного выбора 12 Лабораторная работа 5.1 (на один вопрос – много ответов; что же выбрать?) 12 6. Логические переменные и операции 13 Лабораторная работа 6.1 (таблица истинности) 13 Лабораторная работа 6.2 (бросаем точку на плоскость и наблюдаем за ней) 14 Лабораторная работа 6.3 (составляем логические условия) 16 7. Операторы цикла 17 Лабораторная работа 7.1 (вычисляем суммы и произведения конечных рядов) 17 Лабораторная работа 7.2 (оператор цикла с предусловием – исследуем числа) 17 Лабораторная работа 7.3 (еще раз тренируемся в использовании оператора цикла) 18 Лабораторная работа 7.4 (факториал, Фибоначчи, Евклид и...) 20 Лабораторная работа 7.5 (обрабатываем последовательности) 21 Лабораторная работа 7.6 (препарируем целые числа) 22 Лабораторная работа 7.7 (опять целые числа, но мастерство – на ступень выше) 23 8. Символьные данные 24 Лабораторная работа 8.1 (узнаем у компьютера, какими он пользуется символами) 24 Лабораторная работа 8.2 (впервые обрабатываем не числа, а текст) 24 9. Подпрограммы (процедуры и функции) 25 Лабораторная работа 9.1 (задачи знакомые, но записываем их в новой форме) 25 10. Численные методы 27 Лабораторная работа 10.1 (приближенно решаем уравнения) 27 Лабораторная работа 10.2 (приближенно находим пло
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.222.102 (0.013 с.) |

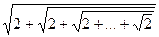 – всего N корней.
– всего N корней.























 1
1







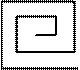






























































 9
9




















 13
13



