
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические переменные и операцииСодержание книги
Поиск на нашем сайте
Лабораторная работа 5.1 (таблица истинности)
Переменные x, y и z – переменные логического типа. Написать программу, строящую расширенную таблицу истинности для вычисления формулы:
1. x and not y or (z and x) 2. x and y or (not z and x) 3. y and not y or (z and x) 4. x or (not y or (z and x)) 5. x or y and (z and not x) 6. x and not y or (z and x) 7. not (x and y and z) or (not z and x) 8. x and not y or (z and x) 9. not x and (not y or (z and x)) 10. x and not y and (z or x) 11. x and not z or (y and x) 12. x or (z and x and not y) 13. not x and not y or (z and x) 14. x or y or (not z and x) 15. x and not y and (not z or not x) 16. x or not x or (not z and y and x)
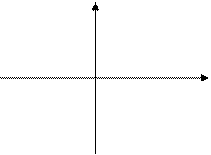
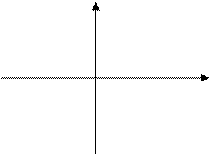
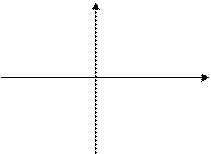
Лабораторная работа 5.2 (бросаем точку на плоскость и наблюдаем за ней)
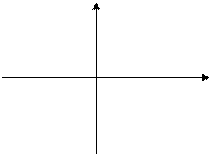
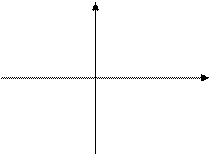
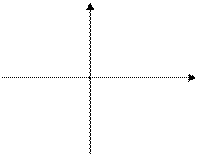
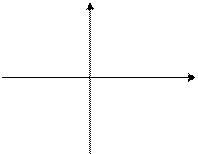
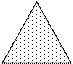
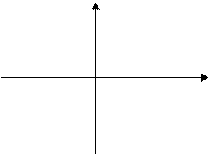
Вводятся координаты точки на плоскости. Определить, попадает ли эта точка в заштрихованную область.
Лабораторная работа 5.3 (составляем логические условия)
Записать логическое выражение, которое имеет значение «истина» только при выполнении следующего условия: 1. Каждое из чисел X и Y больше 100. 2. Только одно из чисел X и Y четное. 3. Неверно, что X>2. 4. Неверно, что X>0 и X<5. 5. Только одно из чисел X, Y и Z меньше 20. 6. Целое N кратно двум или трем. 7. Целое N не кратно трем и оканчивается нулем. 8. Целое N кратно двум и не кратно семи. 9. Каждое из чисел X, Y и Z отрицательное. 10. Числа A, B и C могут являться длинами сторон треугольника. 11. X>2 и Y<3. 12. X>3 или X<-2. 13. Каждое из трёх чисел кратно трем. 14. Только одно из трёх чисел кратно пяти. 15. Только одно из чисел X, Y и Z отрицательное. 16. X>5 и X<1.
Операторы цикла Лабораторная работа 6.1 (вычисляем суммы и произведения конечных рядов)
Вводятся действительные a и x и натуральное n. Вычислить Y:
1. Y= sin (x) + sin(x2) + … + sin(xn). 2. Y= cos(x) + cos(2x) + … + cos(nx). 3. Y= x + x/2 + x/3 + … + x/n. 4. Y= x + x2 + x3 + … + xn. 5. Y= x + x2/2 + x3/3 + … +xn/n. 6. Y= x + x3/3 + x5/5 + … + x2n-1/(2n-1). 7. Y= a + x2/2 + x4/4 + … + x2n/2n. 8. Y= nxn-1 + (n-1)xn-2 + … + 2x + 1. 9. Y= x + (1+2)x2 + (1+2+3)x3 + … +(1+2+3+…+n)xn. 10. Y= 1! + 2! + … + n!. 11. Y= (1+sin(0.1)) (2+sin(0.2)) … (n+sin(n/10)). 12. Y= x(x+1) (x+2) … (x+n-1). 13. Y= 1/sin(1) + 2/(sin(1)+sin(2)) + … +n/(sin(1)+sin(2)+…+sin(n)). 14. Y= x - x2 + x3 – x4 + … + (-1)xn. 15. Y= -x + x2 - x3 + … + (-1)xn. 16. Y= nx + (n-1)x2 + (n-2)x3 +… + xn.
Лабораторная работа 6.2 (оператор цикла с предусловием – исследуем числа)
Вводится последовательность положительных целых чисел, за которой следует 0 (признак конца последовательности). Определить сумму чисел, их количество, минимальное и максимальное число с их порядковыми номерами среди тех введенных чисел, которые обладают следующими свойствами:
1. находятся между 11 и 99; 2. имеют четный порядковый номер ввода; 3. кратны пяти; 4. оканчиваются на цифру нуль; 5. имеют нечетный порядковый номер ввода; 6. четные; 7. оканчиваются на цифру семь; 8. нечетные; 9. оканчиваются на цифру один; 10. оканчиваются на цифру три; 11. кратны семи; 12. кратны трем; 13. оканчиваются на цифру пять; 14. однозначные; 15. двузначные; 16. трехзначные;
Лабораторная работа 6.3 (еще раз тренируемся в использовании оператора цикла)
1. Даны натуральные числа x и y. Найти произведение x*y, используя лишь операцию сложения. Задачу решить двумя способами (первый способ – x*y, второй – y*x). 2. Составить программу возведения натурального числа в квадрат, учитывая следующую закономерность: 3. Найти сумму 12+22+32+…+102. Учесть особенности получения квадрата натурального числа, отмеченные в предыдущей задаче. 4. Составить программу возведения натурального числа в третью степень, учитывая следующую закономерность: 5. Одноклеточная амеба каждые три часа делится на две клетки. Определить, сколько клеток будет через 3, 6, 9, …, 24 часа, если первоначально была одна амеба. 6. Ученик A открыл первого сентября счет в банке, вложив X рублей. Каждый месяц размер вклада увеличивается на 2% от текущей суммы. Какой суммой денег будет располагать ученик к концу июня, чтобы отпраздновать успешное окончание учебного года? 7. Вводится натуральное число N. Вычислить:
8. На полу около стенки наклонно стоит палка длиной L метров. Нижний конец находится на расстоянии X метров от стенки. Палка начинает скользить и падает на пол. Определить значение угла между палкой и полом (в градусах) с момента начала скольжения до падения палки через каждые 0.1 метра. 9. В сентябре поступивший в школу №1580 ученик идет от дома до школы прогулочным шагом со скоростью 3 км/час и тратит на это путешествие t часов времени. Но количество задаваемых на дом работ увеличивается каждый месяц на 3% по отношению к предыдущему месяцу, и в таком же соотношении увеличивается скорость ученика. Спрашивается, с какой скоростью и за какое время он будет пробегать этот же путь в конце мая. 10. Определить суммарный объем в литрах 12 вложенных друг в друга шаров со стенками толщиной 5 мм. Внутренний диаметр внутреннего шара равен 10 см. Принять, что шары вкладываются друг в друга без зазоров. 11. В некоторой стране используются купюры следующего достоинства 1, 2, 4, 8, 16, 32 и 64 единиц. Как наименьшим количеством купюр можно расплатиться за товар стоимостью в N единиц (указать количество каждой из купюр). Считаем, что имеется достаточное количество купюр всех достоинств. 12. Начав тренировки, лыжник в первый день пробежал 10 км. Каждый следующий день он увеличивал длину пробега на 10% от пробега предыдущего дня. Определить: 13. Вводится действительное число A.
Лабораторная работа 6.4 (факториал, Фибоначчи, Евклид и...)
1. Вводится натуральное число. Определить, является ли оно простым. 2. Вводится натуральное число n. Вычислить его факториал (n!). 3. Вводятся натуральные n и k. Вычислить nk. 4. Вводится радиус круга R. Подсчитать, сколько точек с целочисленными координатами попадают в круг радиуса R с центром в начале координат. 5. Вводится натуральное n. Получить наименьшее число вида 2R, превосходящее n. 6. Вводится натуральное число n. Определить, является ли оно совершенным. Например 6 – совершенное число, т.к. 6=1+2+3. 7. Вычислить наименьшее общее кратное двух чисел, используя алгоритм Евклида для вычисления их наибольшего общего делителя. 8. Даны натуральные числа a и b, являющиеся соответственно числителем и знаменателем дроби. Сократить дробь, найдя наибольший общий делитель (НОД(a,b)) по алгоритму Евклида. 9. Даны натуральные числа a и b (a>b). Найти результат и остаток целочисленного деления a на b, не используя стандартных операций DIV и MOD. 10. Вводится натуральное число n. Найти n-ое число Фибоначчи. 11. Вводится натуральное число n. Найти сумму первых n чисел Фибоначчи. 12. Задан прямоугольник размером A*B (A и B- натуральные). От прямоугольника каждый раз отрезаются квадраты максимальной площади. Найти общее количество квадратов. 13. Вводятся три натуральных числа a, b и c. Найти их наибольший общий делитель по алгоритму Евклида, учитывая, что НОД(a,b,c)=НОД(НОД(a,b),c). 14. Вводятся два натуральных числа. Найти их наибольший общий делитель по алгоритму Евклида. 15. Вводится факториал некоторого числа N. Найти число N.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.247.255 (0.007 с.) |






 3
3





 5
5
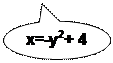


 7
7






 9
9




 11
11









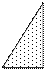

 13
13









 15
15
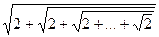 – всего N корней.
– всего N корней.


