Анализ результатов решения задачи

Результаты реализации экономико-математической модели по оптимизации отраслевой структуры производства приведены в таблице 9.

Таблица 9. Результаты решения задачи по оптимизации отраслевой

структуры производства

Номер переменной	Наименование переменной	Значение по решению
x1	Озимая пшеница товарная	1 386,2
x2	Озимая пшеница фуражная	0,0
x3	Ячмень товарный	449,7
x4	Ячмень фуражный	24,6
x5	Соя	1 000,0
x6	Горчица	0,0
x7	Сахарная свекла	750,0
x8	Подсолнечник	625,0
x9	Кукуруза на силос	113,4
x10	Кукуруза на зеленый корм 1-го срока сева	2,1
x11	Кукуруза на зеленый корм 2-го срока сева	1,0
x12	Однолетние травы на сено	0,0
x13	Однолетние травы на сенаж	0,0
x14	Однолетние травы на зеленый корм 1 срока сева	2,4
x15	Однолетние травы на зеленый корм 2 срока сева	3,3
x16	Многолетние травы на сено	133,9
x17	Многолетние травы на сенаж	253,3
x18	Многолетние травы на зеленый корм	2,0
x19	Озимые на зеленый корм	3,0
x20	Пар	250,0
x21	Комбикорм	3 274,0
x22	Патока	1 823,9
x23	Премикс	178,0
x24	Молоко на корм	125,0
x25	Обрат	365,4
x26	ЗЦМ	28,0
x27	Поголовье крупного рогатого скота	400,0
x28	Сумма производственных затрат	81 764,0

В результате решения задачи были определены площади посева сельскохозяйственных культур, объемы приобретаемых кормов и кормовых добавок, поголовье крупного рогатого скота (в структурных головах) и сумм производственных затрат по предприятию.

Все ограничения выполнены. Анализируя результаты, представленные в столбце «Сумма произведений» можно сделать следующие выводы.

Имеющаяся в хозяйстве пашня используется полностью.

Площадь посева зерновых и зернобобовых (ограничения 3 и 4) по оптимальному решению составляет 2 863,5 га. Площадь озимых культур (ограничения 3 и 4) формируется на уровне 1 389,3 га (при нижней и верхней границе соответственно 1 000 и 1 500 га). Максимально возможных значений достигает площадь сахарной свеклы, подсолнечника и сои (соответственно 750, 625 и 1 000 га). Площадь пара берется по минимально допустимой границе в 250 га.

Все озимые культуры размещены по хорошим предшественникам. Излишки площадей по таким культурам отсутствуют.

Таблица 10. Выполнение договорных обязательств по реализации продукции, ц

Продукция	Объемы реализации по плану	Объемы реализации по решению	Объемы реализации сверх плана
Пшеница	23 000	48 158	25 158
Ячмень	12 000	13 500	1 500
Сахарная свекла	95 000	337 500	242 500
Молоко	20 000	20 315

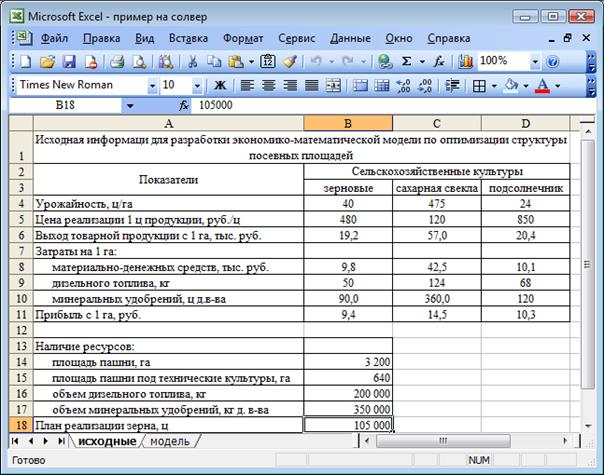
Если реализация пшеницы, ячменя и сахарной свеклы сверх плана объясняется выгодностью данных видов продукции, то перевыполнение плана по молоку связано с тем, что поголовье крупного рогатого скота было зафиксировано на фактическом уровне.

Анализ обеспеченности отрасли животноводства кормами показывает, что по оптимальному решению излишек кормов составит 8 314,1 ц к.ед. Этот излишек образуется за счет соломы, которая является побочной продукцией при производстве зерновых и зернобобовых культур. Наблюдается избыток в рационе переваримого протеина (около 49 т), что свидетельствует о необходимости корректировки рационов кормления.

Сумма чистого дохода по оптимальному решению составляет 35 761,7 тыс. руб., а уровень рентабельности – 43,7%.

4. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
С ПОМОЩЬЮ MICROSOFT EXCEL

4.1. Пример решения задачи линейного программирования

Сельскохозяйственное предприятие специализируется на производстве зерна, сахарной свеклы и подсолнечника. Для возделывания этих сельскохозяйственных культур может быть выделено до 3 200 га пашни, дизельного топлива в объеме до 200 000 кг и минеральных удобрений в объеме до 400 000 кг действующего вещества. Требуется найти такое сочетание посевных площадей, которое обеспечило бы получение максимума прибыли.

Следует также учесть, что:

· площадь посева технических культур (сахарной свеклы и подсолнечника) не должна превышать 20% общей площади пашни;

· предприятием заключен договор на продажу зерна в объеме 105 000 ц.

Входная информация, необходимая для разработки экономико-математической модели приведена в таблице 13.

Таблица 13. Входная информация для разработки экономико-математической модели

Показатели	Сельскохозяйственные культуры
зерновые	сахарная свекла	подсолнечник
Урожайность, ц/га
Цена реализации 1 ц продукции, руб./ц
Выход товарной продукции с 1 га, тыс. руб.	19,2	57,0	20,4
Затраты на 1 га: материально-денежных средств, тыс. руб.	9,8	42,5	10,1
дизельного топлива, кг
минеральных удобрений, кг д. в-ва	90,0	360,0
Прибыль с 1 га, руб.	9,4	14,5	10,3

За неизвестные примем площади посева сельскохозяйственных культур по видам:

X₁ - зерновых культур;

X₂ - сахарной свеклы;

X₃ – подсолнечника.

Для построения экономико-математической модели задачи необходимо учесть все условия. В данном случае по этим условиям можно составить пять ограничений:

- сумма площадей посева сельскохозяйственных культур не должна превышать площади, имеющейся в предприятии (3 200 га). Коэффициенты при неизвестных характеризуют расход пашни на возделывание 1 га соответствующей сельскохозяйственной культуры. В правой части ограничения указывается объем площади пашни

1) Х₁+Х₂+Х₃<=3 200;

- сумма площадей посева технических культур не должна превышать площади, которая может быть отведена для этой цели (3200·20%=640 га). Коэффициенты при неизвестных характеризуют расход пашни, отводимой под технические культуры, на возделывание 1 га соответствующей технической культуры. В правой части ограничения указывается объем площади пашни, которая может быть отведена под технические культуры.

2) Х2+Х3<=640;

- третье и четвертое ограничения гарантируют, что использование ресурсов не превысит их наличия. То есть сумма произведений затрат ресурсов на 1 га на площади посева соответствующих сельскохозяйственных культур не должна превышать объемов ресурсов, имеющихся в предприятии. Коэффициенты при неизвестных характеризуют расход соответствующего ресурса на возделывание 1 га соответствующей сельскохозяйственной культуры. В правой части ограничений указывается наличие этих ресурсов в хозяйстве:

3) 50Х1+ 124Х2+68Х3<=200 000;

4) 90Х1+360Х2+120Х3<=350 000;

- пятое ограничение гарантирует производство запланированного объема реализации зерна. В качестве коэффициентов при переменных выступает выход зерна с 1 га площади посева зерновых культур. В правой части указывается запланированный объем реализации зерна

5) 40Х1>=105 000.

В результате получена система пяти линейных неравенств с тремя неизвестными. Требуется найти такие неотрицательные значения этих неизвестных Х₁>=0; Х₂>=0; Х₃>=0, которые бы удовлетворяли данной системе неравенств и обеспечивали получение максимума прибыли:

Zmax = 9,4Х1+14,5Х2+10,3Х3.

В качестве коэффициентов при неизвестных в целевой функции выступает прибыль, получаемая с 1 га площади посева сельскохозяйственных культур.

Поскольку данная задача решается с помощью MS Excel, то и подготовку всей входной информации для построения экономико-математической модели целесообразно осуществлять также с использованием этого табличного процессора. Эти расчеты представлены на листе «Исходные» файла MS Excel (рисунок 1). Это не только облегчает расчеты, связанные с подготовкой входной информации, но и дает возможность в дальнейшем автоматически обновлять параметры экономико-математической модели при реализации различных вариантов.

Рисунок 1. Входная информация для разработки экономико-математической модели

 

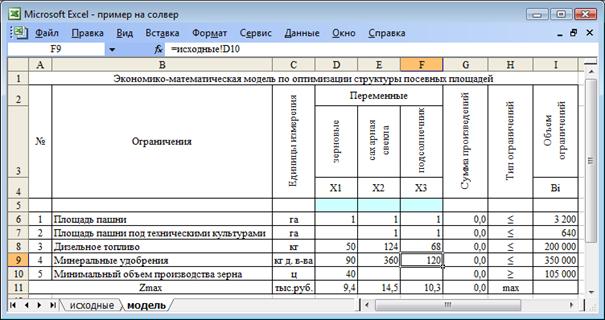
Рисунок 2. Экономико-математическая модель по оптимизации структуры посевных площадей

Экономико-математическая модель по оптимизации структуры посевных площадей в матричном виде заполняется на листе «Модель» файла MS Excel, уже содержащего лист «Исходные» (рисунок 2). Технико-экономические коэффициенты, оценки целевой функции (столбцы D, E, F), объемы ограничений (столбец I) рекомендуется определять через ссылки на соответствующие ячейки листа «Исходные».

На рисунке 2 показано, каким образом произошло заполнение ячейки F9, описывающей затраты минеральных удобрений на 1 га посева подсолнечника (смотри строку «f_x» рисунка 1).

В столбцы А (№), В (Ограничения), С (Единицы измерения) и H (Тип ограничений) вводятся соответствующие данные в текстовом формате. Они не используются в расчетах и служат для информативности и облегчения понимания содержания модели.

Для искомых величин переменных Х₁, Х₂, Х₃ необходимо оставить пустые ячейки соответственно D5, E5, F5. Столбец G (Сумма произведений), предназначен для определения суммы произведений значений искомых неизвестных (ячейки D5, E5, F5) и технико-экономических коэффициентов по соответствующим ограничениям (строки 6-10) и целевой функции (строка 11).

Формула нахождения суммы произведений для строки с целевой функцией (для ячейки G11) приведена в верхней строке рисунка 3.

 

Рисунок 3. Экономико-математическая модель по оптимизации структуры посевных площадей

То есть, в столбце G будут определяться:

· количество используемых ресурсов (ячейка G6 – общей площади пашни; G7 – пашни, которая может быть использована под посевы технических культур; G8 – трудовых ресурсов; G9 – минеральных удобрений);

· количество произведенного зерна (ячейка G10);

· величина прибыли (ячейка G11).

Таким образом, построен опорный план и получено первое допустимое решение. Значения неизвестных Х₁, Х₂, Х₃ равны нулю (ячейки D5, E5, F5 - пустые ячейки), ячейки столбца G «Сумма произведений» по всем ограничениям (строкам 6-10) и целевой строке (строка 11) также имеют нулевые значения.

Для оптимизации имеющегося плана воспользуемся инструментом Поиск решения, который находится в меню Сервис. Если нет такой команды в меню Сервис, необходимо в пункте Надстройка поставить галочку напротив Поиск решения. После этого данная процедура станет доступной в меню Сервис.

После выбора команды Поиск решения появится диалоговое окно.

Рисунок 4. Диалоговое окно команды Поиск решения

Поскольку в качестве критерия оптимизации нами выбрана максимизация прибыли, в поле Установить целевую ячейку необходимо ввести ссылку на ячейку, содержащую формулу расчета прибыли. В нашем случае это ячейка $G$11.

Рисунок 5. Диалоговое окно команды Поиск решения

Чтобы максимизировать значение конечной ячейки путем изменения значений влияющих ячеек (влияющими, в данном случае это и изменяемые ячейки, являются ячейки, которые предназначены для хранения значений искомых неизвестных), переключатель необходимо установить в положение Равной максимальному значению.

В поле Изменяя ячейки необходимо ввести ссылки на изменяемые ячейки, разделяя их запятыми, либо, если ячейки находятся рядом, указывая первую и последнюю ячейку, разделяя их двоеточием ($D$5:$F$5).

Рисунок 6. Диалоговое окно команды Поиск решения

В поле Ограничения необходимо ввести все ограничения, накладываемые на поиск решения.

В разделе Ограничения диалогового окна команды Поиск решения необходимо выбрать функцию Добавить. Появится следующее диалоговое окно.

Рисунок 7. Диалоговое окно команды Добавление ограничения

Добавление ограничений рассмотрим на примере всех ограничений. В поле Ссылка на ячейку необходимо ввести адрес одной ячейки (совокупности ячеек), на которую накладываются ограничения. В нашем случае это ячейки $G$6:$G$9, в которых находятся формулы расчета количества используемых ресурсов. Затем из раскрывающегося списка условных операторов необходимо выбрать необходимый знак, который должен располагаться между ссылкой на ячейку и ограничением. В нашем случае, это <=. В поле Ограничение необходимо ввести ссылки на ячейки, в которых находятся значения, характеризующие наличие ресурсов. В нашем случае это ячейки $I$6:$I$9.

В результате диалоговое окно примет следующий вид.

Рисунок 8. Диалоговое окно команды Добавление ограничения

После подтверждения добавления описанных ограничений (необходимо нажать кнопку Добавить), аналогично добавляется ограничение по обеспечению минимального объема производства зерна (строка 10).

Рисунок 9. Диалоговое окно команды Добавление ограничения

После описания последнего ограничения необходимо вернуться в диалоговое окно команды Поиск решения, нажав виртуальную кнопку OK.

Рисунок 10. Диалоговое окно команды Добавление ограничения

В случае внесения изменения в какое-либо из ограничений, необходимо выделить его в списке Ограничения и выбрать команду Изменить. Аналогичным способом можно удалить ненужное ограничение.

После добавления ограничений описываются параметры поиска решения. Для этого в диалоговом окне команды Поиск решения выбирается команда Параметры (рисунок 11).

Опция Линейная модель в диалоговом окне команды Параметры поиска решения служит для ускорения поиска решения линейной задачи оптимизации.

Опция Неотрицательные значения позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение.

Остальные параметры можно оставить без изменений либо установить необходимые параметры, используя опцию Справка.

Выбор параметров подтверждается нажатием виртуальной кнопки ОК.

Рисунок 11. Диалоговое окно команды Параметры поиска решения

Для запуска задачи на решение необходимо нажать виртуальную кнопку Выполнить диалогового окна команды Поиск решения.

Рисунок 12. Диалоговое окно команды Результаты поиска решения

Для сохранения найденного решения на листе необходимо выбрать в диалоговом окне Результаты поиска решения опцию Сохранить найденное решение.

Для восстановления исходных данных применяется опция Восстановить исходные значения диалогового окна Результаты поиска решения.

Прерывание поиска решения осуществляется нажатием клавиши ESC.

В результате решения и сохранения результатов поиска модель примет вид, представленный на рисунке 13.

В ячейках D5:F5получены значения искомых неизвестных (площади посева равны: зерновых ‑ 2 625,0 га, сахарной свеклы – 186,5 га, подсолнечника – 388,5 га), в ячейках G6:G9 определены объемы используемых ресурсов (общей площади пашни – 3200 га; площади пашни, которая будет использоваться под посевы технических культур, – 575 га; дизельного топлива – 180 791,7 кг; минеральных удобрений – 350 000 кг д. в-ва), в ячейке G10 найдено количество зерна, которое может быть реализовано, ‑ 105 000 ц). При этом величина прибыли достигает 31 380,6 тыс. руб. (ячейка G11).

Рисунок 13. Экономико-математическая модель по оптимизации структуры посевных площадей с результатами решения

В случае если в результате поиска не было найдено решение, удовлетворяющее заданным условиям, в диалоговом окне Результаты поиска решения появится соответствующее сообщение

Рисунок 14. Диалоговое окно команды Результаты поиска решения

Одной из наиболее часто встречающихся причин невозможности найти оптимальное решение является невыполнение одного или нескольких ограничений. Сохранив найденное решение, требуется построчно сравнить полученные значения столбцов «Сумма произведений» и «Объем ограничений» и проверить, удовлетворяет ли отношение между ними ограничению, стоящему в столбце «Тип ограничений». Определив, таким образом, невыполняемые ограничения, необходимо найти и ликвидировать причины, обусловливающие невозможность соблюдения данного конкретного условия (это может быть, например, слишком большие или, наоборот, очень маленькие запланированные объемы ограничений и т.п.).

4.2. Анализ результатов решения задачи на основе стандартных отчетов MS Excel

Наряду с получением оптимального решения Надстройка MS Excel позволяет получить три стандартных отчета, которые могут использоваться для анализа результатов решения экономико-матема-тической задачи. Это отчет по результатам, отчет по устойчивости и отчет по пределам.

Формирование отчетов происходит с помощью диалогового окна Результаты поиска решения путем выбора соответствующего пункта меню Тип отчета. Для создания нужного отчета необходимо выделить мышью его название. Для выделения нескольких отчетов следует использовать мышь одновременно с нажатой клавишей Ctrl. Выбор отчетов подтверждается нажатием виртуальной кнопки ОК. Каждый сформированный отчет размещается на отдельном листе текущей книги.

Отчет по результатам состоит из трех частей и содержит информацию о целевой функции; о значениях переменных, полученных в результате решения задачи; об ограничениях.

В отчете по результатам представлена информация:

- о целевой функции и изменяемых ячейках (переменных): адреса ячеек, используемых для вычисления значений; имена; исходные значения (до решения задачи) и значения при оптимальном решении;

- об ограничениях: адреса ячеек, используемых для вычисления значений; имена; значения при оптимальном решении; формулы, соответствующие левым частям ограничений; статус ограничений (характеристика степени использования конкретного ресурса) и разница (количественная характеристика недоиспользованных объемов ресурсов).

Отчет по результатам для задачи, описанной в подразделе 5.1., приведен на рисунке 1.

Рисунок 1. Отчет по результатам

На основании данного отчета можно сделать следующие выводы:

- полученный оптимальный план обеспечивает при заданном уровне прибыльности отдельных сельскохозяйственных культур получение прибыли в сумме 31 380,6 тыс. руб.;

- получение максимально возможной суммы прибыли возможно при размещении посевов озимой пшеницы на площади 2 625,0 га, сахарной свеклы – 186,5 га, подсолнечника – 388,5 га;

- полностью используются (т.е. являются дефицитными) такие ресурсы как вся пашня и минеральные удобрения, а объем производства озимой пшеницы по оптимальному решению не превышает минимально необходимого;

- остаются недоиспользованными такие ресурсы, как пашня, отводимая под технические культуры (65 га) и дизельное топливо (19 208,3 кг).

ОБРАТИТЕ ВНИМАНИЕ: Если ресурс используется полностью (то есть ресурс дефицитный) или левая часть ограничения строго равна правой части, то в графе «Статус» соответствующее ограничение описывается как «связанное»; при неполном использовании ресурса (то есть в случае если ресурс недефицитен) или неравенстве левых и правых частей ограничений в этой графе указывается «не связан.».

Отчет по устойчивости состоит из двух частей и содержит информацию об изменяемых ячейках и ограничениях.

В отчете по устойчивости представлена информация:

- об изменяемых ячейках (переменных): адреса ячеек, используемых для вычисления значений; имена; результирующие значения (при оптимальном решении); нормированная стоимость; коэффициент целевой функции; предельно допустимые величины увеличения и уменьшения коэффициентов целевой функции, при которых сохраняется базис оптимального решения;

- об ограничениях: адреса ячеек, используемых для вычисления значений; имена; результирующие значения (при оптимальном решении); теневые цены (двойственная оценка, оценка влияния изменения ресурса на изменение целевой функции); исходные запасы ресурсов или объемы прочих ограничений; предельно допустимые величины увеличение и уменьшение объемов ограничений, при которых остается неизменным уровень теневой цены для данного ограничения.

Отчет по устойчивости для анализируемой задачи приведен на рисунке 2.

Рисунок 2. Отчет по устойчивости

Поскольку все переменные вошли в базисное решение, то нормированная стоимость по всем неизвестным равна нулю.

ОБРАТИТЕ ВНИМАНИЕ: В случае если какая-либо переменная не вошла бы в базисное решение, то нормированная стоимость показала бы, на сколько изменится целевая функция при принудительном включении единицы этой сельскохозяйственной культуры в оптимальное решение.

По переменным Х₂ (площадь посева сахарной свеклы) и Х₃ (площадь посева подсолнечника)коэффициенты целевой функции (прибыль в расчете на 1 га посева) могут быть увеличены соответственно на 3 и 4,2 тыс. руб. или уменьшены соответственно на 4,2 и 0,333333333 тыс. руб. без изменения базиса оптимального решения (найденной оптимальной структуры посевных площадей). То есть указанные пределы описывают границы изменения прибыльности, за которыми меняется оценка экономической целесообразности возделывания сахарной свеклы и подсолнечника.

По переменной Х₁ допустимое уменьшение является бесконечно большой величиной[7]. Это связано с тем, что для выполнения всех ограничений площадь посева озимой пшеницы не может быть меньше, чем по оптимальному решению, и падение прибыльности данной сельскохозяйственной культуры никак не повлияет на структуру посевных площадей. С другой стороны, при росте прибыльности озимой пшеницы более чем на 0,375 тыс. руб. эта культура становится экономически привлекательной, что обуславливает возможный рост ее доли в структуре посевных площадей.

При анализе отчета по ограничениям основное внимание уделяется теневым ценам и допустимым пределам изменения объемов ограничений.

ОБРАТИТЕ ВНИМАНИЕ: При формировании столбца «Теневая цена» все ячейки по умолчанию имеют формат целых чисел. В этой связи после формирования отчета измените формат ячеек, увеличив число десятичных знаков до 4-5.

Теневые цены, по сути, могут служить ориентиром при принятии решения о дополнительном привлечении ресурсов или наращивании объемов производства того или иного вида продукции.

Так по ресурсам, которые не являются дефицитными (пашня, отводимая под технические культуры, и дизельное топливо), теневые цены равны нулю.

Введение в хозяйственный оборот дополнительно 1 га пашни при заданном уровне прибыльности сельскохозяйственных культур обеспечит рост целевой функции на 8,2 тыс. руб. Причем, этот уровень теневой цена будет сохраняться при отклонениях площади пашни от оптимального решения от минус 259,0278 га до плюс 65 га.

Дополнительное приобретение 1 кг минеральных удобрений обуславливает рост целевой функции на 0,0175 тыс. руб. Данное влияние на объем прибыли сохранится при отклонении объема приобретаемых удобрений от значения по оптимальному решению от минус 44 750 кг до плюс 82 321,4286 кг.

Таким образом, теневая цена ограничений по использованию ресурсов служит своеобразным критерием оценки целесообразности вовлечения в производство дополнительного объема того или иного вида ресурсов. Так экономически целесообразно вовлекать дополнительно в процесс производства до 65 га пашни при условии, что плата за использование ее 1 га не превысит 8,2 тыс. руб. Дополнительное приобретение минеральных удобрений в объеме 82 321 разумно при цене минеральных удобрений не выше 17,5 тыс. руб. за 1 т.

Теневая цена по ограничению, связанному с определением объема озимой пшеницы, свидетельствует о том, что производство каждого дополнительного центнера зерна пшеницы будет снижать размер прибыли по предприятию на 0,0094 тыс. руб. Критичными для данного уровня влияния объемов производства озимой пшеницы на целевую функцию будут отклонения от минус 2 600 ц до плюс 13814,8148 ц.

Отчет по пределам состоит из двух частей и содержит информацию о ячейке, описывающей целевую функцию, и ячейках, описывающих переменные.

В отчете по пределам представлена информация:

- о ячейке, описывающей целевую функцию: адрес ячейки, имя целевой функции; значение целевой функции при оптимальном решении;

- о ячейках, описывающих переменные: адреса ячеек, используемых для вычисления значений переменных; имена; значения переменных при оптимальном решении; значения нижних и верхних пределов, которые может содержать влияющая ячейка при условии фиксированности значений остальных ячеек и их удовлетворения наложенным ограничениям; целевой результат при достижении верхних и нижних пределов.

Отчет по пределам для анализируемой задачи приведен на рисунке 3.

Целевой результат по нижнему пределу отражает объем прибыли, который может быть получен при достижении площадей каждой сельскохозяйственной культуры указанных в отчете нижних пределов.

Рисунок 3. Отчет по пределам

Так, при полном отказе от возделывания сахарной свеклы максимальная сумма прибыли составит 28 677 тыс. руб., при полном отказе от возделывания подсолнечника – 27 378,6 тыс. руб. По озимой пшенице значение целевой функции остается неизменным, поскольку сократить площадь ее посева ниже 2 625 га невозможно, поскольку в этом случае не будет выполнено условие по минимально необходимому объему производства озимой пшеницы, т.е. задача не будет иметь решения.

Верхний предел характеризует наибольшее значение, которое могут иметь изменяемые ячейки при условии, что все ограничения выполняются, а значения остальных изменяемых ячеек фиксированы (равны оптимальным). Как правило, в случае решения задачи на максимум все верхние пределы изменяемых ячеек соответствуют значениям переменных по оптимальному решению, так же как и значения целевой функции.

 

ПРИЛОЖЕНИЯ

 

Приложение 1

 

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное образовательное учреждение
высшего профессионального образования

«Воронежский государственный аграрный университет им. К.Д. Глинки»

Кафедра информационного обеспечения и моделирования агроэкономических систем

КУРСОВОЙ ПРОЕКТ

по дисциплине

«Моделирование социально-экономических систем и процессов»

на тему «Обоснование оптимальных параметров развития сельскохозяйственных предприятий»

Выполнил

студент 3 курса дистанционной формы обучения (Усманское представительство).

Проскурин С.А.

Специальность: 080502: экономика и управление на предприятии агропромышленного комплекса

 

Руководитель: д.э.н., профессор

Улезько А.В.

Воронеж
2010

Приложение 2

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.............................................................................................. 3

1. Математическое моделирование экономических систем 5

1.1. Экономико-математические модели: сущность и классификация... 5

1.2. Этапы экономико-математического моделирования..................... 13

3. ОПТИМИЗАЦИЯ ПАРМЕТРОВ РАЗВИТИЯ ООО «простор».. 37

3.1. Постановка и условия задачи, подготовка входной информации 37

3.2. Разработка экономико-математической модели по оптимизации отраслевой структуры производства................................................................................. 51

3.3. Анализ результатов решения......................................................... 51

ВЫВОДЫ И ПРЕДЛОЖЕНИЯ........................................................... 58

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.......................... 59

ПРИЛОЖЕНИЯ..................................................................................... 60

Приложение 3

Библиографическое описание монографий, учебников или учебных пособий
от 1-го до 3-х авторов.

1. Улезько А.В. Стратегия формирования и тактика использования ресурсного потенциала сельскохозяйственных предприятий. Воронеж: ГП «ИПФ «Воронеж», 2004. 224 с.

2. Курносов А.П., Черных А.Н., Кузнецова Е.Д. Оптимизация параметров развития сельскохозяйственных предприятий в условиях государственного регулирования АПК. ФГОУ ВПО Воронежский ГАУ, 2010. 191 с.

Библиографическое описание монографий, учебников или учебных пособий
более 3-х авторов.

3. Оптимизация параметров функционирования сельскохозяйственных предприятий при изменяющихся условиях хозяйствования / А.П. Курносов, А.В. Улезько, А.К. Камалян и др. М.: Изд-во Московского государственного социального университета «Союз», 2000. 163 с.