
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатель точности оценки параметровСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Сама по себе абсолютная величина выборочной ошибки как показатель именованный мало пригодна для случаев сравнительной оценки точности, с какой определены средние результаты наблюдений по отношению их к генеральным параметрам, в случае, если средние с их ошибками выражены в разных единицах измерения. Чтобы получить определенное представление о точности, с какой определен тот или иной результат, принято использовать так называемый показатель точности (CS). Когда известно значение коэффициента вариации V %, показатель точности можно определить по следующей формуле:
Известно, что под точностью определения выборочной средней понимается степень приближения ее к средней генеральной совокупности. Чем точнее определен средний результат, тем меньше будет CS и наоборот, при менее точном среднем результате показатель CS окажется больше. Точность считается достаточной, если CS не превышает 5 %. Если проводят очень важные испытания, связанные с жизнью человека, то CS не превышает 3 %.
Порядок работы на II этапе 1. Ознакомиться с ситуацией и организацией игры на II этапе. 2. Ознакомиться с теоретическими сведениями. 3. Ознакомиться с образцом отчета о работе на II этапе. 4. Рассчитать основные статистические характеристики выборок. 5. Построить основные графики вариационного ряда (полигон распределения, гистограмма распределения) для выборки А. 6. Оформить отчет о проделанной работе (по образцу, приведенному далее).
Отчет Тема: Математические методы статистической обработки результатов измерений в спорте. Цели: 1. Ознакомиться с наиболее распространенными методами статистической обработки результатов измерений в физическом воспитании и спорте. 2. Приобрести навыки расчета основных статистических характеристик выборки. 3. Научиться строить основные графики вариационного ряда (полигон распределения, гистограмма распределения). Вопросы: 1. Предмет математической статистики. 2. Этапы статистического обследования. 3. Дискретные и непрерывные ряды. 4. Выборочная и генеральная совокупности. Объем выборки. 5. Что называют ранжированием ряда? 6. Полигон и гистограмма распределения. 7. Основные статистические характеристики центра ряда. 8. Характеристики вариации. 9. Понятие репрезентативности выборочных показателей, ошибки репрезентативности. Статистическая обработка результатов измерений, (Ф.И.О. студента, пишущего отчет) Расчет основных статистических характеристик выборки А:
Запишем выборку А в порядке возрастания, т.е. ранжированный ряд и найдем моду и медиану. 131, 144, 151, 153, 154, 168, 168, 182, 189, 208. Мода = 168 мс. Медиана = 161 мс. Среднее арифметическое значение выборки А:
Дисперсия:
Среднее квадратическое (стандартное) отклонение:
Стандартная ошибка средней арифметической:
Коэффициент вариации:
Размах варьирования R = 208 – 131 = 77 мс Графическое представление Запишем ранжированный ряд: 131, 144, 151, 153, 154, 168, 168, 182, 189, 208. Т.к. n = 10, по таблице 2.2 находим число интервалов: k = 4. Шаг интервала: Примечание: во избежание ошибок при составлении вариационного ряда шаг интервала надо использовать без округлений или округлять только в большую сторону. Заполним таблицу «Вариационный ряд результатов измерений». Столбец 1. Записываем порядковые номера интервалов. Столбец 2. Нижнюю границу 1-го интервала выбираем равной xmin=131; прибавляем шаг интервала: 131 + 19,25 = 150,25 – верхняя граница 1-го интервала (она же нижняя граница 2-го интервала) и т.д. Столбец 3. Частота интервала равна количеству значений в выборке, которые попали в обозначенный интервал. Первое число включаем в 1-й интервал. Если какое-либо число попало на границу между интервалами, его следует включать в меньший по порядку интервал, например, число на границе 1-го и 2-го интервалов включается в 1-й интервал. Последнее число должно оказаться в последнем интервале. Сумма частот всех интервалов должна быть равна объему выборки. Вариационный ряд результатов измерений
Полигон распределения
Гистограмма распределения
131 150,25 169,5 188,75 208
Расчет основных статистических характеристик выборки Б:
Запишем выборку Б в порядке возрастания, т.е. ранжированный ряд и найдем моду и медиану. 123, 140, 141, 150, 154, 162, 165, 167, 173, 190. Моды нет. Медиана = 158 мс. Среднее арифметическое значение выборки Б:
Дисперсия:
Среднее квадратическое отклонение:
Стандартная ошибка средней арифметической:
Коэффициент вариации:
Размах варьирования R = 190 – 123 = 67 мс
Графическое представление Запишем ранжированный ряд: 123, 141, 142, 150, 154, 162, 163, 167, 173, 190. Шаг интервала: Вариационный ряд результатов измерений
Полигон распределения
Гистограмма распределения
123 139,75 156,5 173,25 190
Расчет основных статистических характеристик выборки В:
Запишем выборку В в порядке возрастания, т.е. ранжированный ряд и найдем моду и медиану. 50, 62, 66, 70, 70, 71, 74, 74, 75, 93. Мода1 = 70 уд. Мода2 = 74 уд. Медиана = 70,5 уд. Среднее арифметическое значение выборки В:
Дисперсия:
Среднее квадратическое отклонение:
Стандартная ошибка средней арифметической:
Коэффициент вариации:
Размах варьирования R = 93 – 50 = 43 уд. Графическое представление Запишем ранжированный ряд: 50, 62, 66, 70, 70, 71, 74, 74, 75, 93. Шаг интервала:
Вариационный ряд результатов измерений
Полигон распределения
Гистограмма распределения
50 60,75 71,5 82,25 93
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 632; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

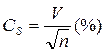 .
.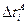 , мс
, мс
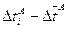 , мс
, мс
 , мс2
, мс2
 = 1648 мс
= 1648 мс
 = 4790 мс2
= 4790 мс2
 мс.
мс. мс2.
мс2.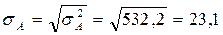 мс.
мс.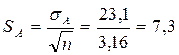 мс.
мс.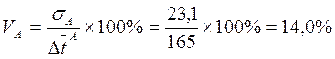 .
. мс.
мс.

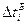 , мс
, мс
 , мс
, мс
 , мс2
, мс2
 = 1565 мс
= 1565 мс
 = 3293 мс2
= 3293 мс2
 мс.
мс.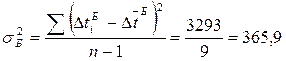 мс2.
мс2.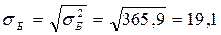 мс.
мс. мс.
мс. .
. мс.
мс.


 , уд.
, уд.
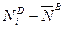 , уд.
, уд.
 , уд.2
, уд.2
 = 705 уд.
= 705 уд.
 = 1067 уд.2
= 1067 уд.2
 уд.
уд. уд2.
уд2. уд.
уд. уд.
уд. .
. уд.
уд.





