
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка эффективности применявшейся методики тренировкиСодержание книги
Поиск на нашем сайте
Для проверки эффективности методики тренировки выдвигаем гипотезы: – нулевую – H0: об отсутствии различия между средним исходным показателем скоростных качеств – конкурирующую – H1: о наличии разницы между ними ( Предположение об ухудшении скоростных качеств после тренировок, т.е. о том, что Ранее мы получили, что sd 2 = 26 уд2. Следовательно,
Наблюдаемое значение t -критерия Стьюдента равно:
По таблице (Приложение 4) ищем tкрит для a = 0,05, числа степеней свободы k = n – 1 = 10 – 1 = 9 и односторонней критической области. Находим, что tкрит = 1,83. Сравнение tнабл и tкрит позволяет сделать вывод: так как tнабл (3,10) > tкрит (1,83), с вероятностью 95% (a = 0,05) должна быть принята конкурирующая гипотеза (H1:
Расчет и построение доверительного интервала для генеральной средней арифметической Так как распределение выборки d, составленной из разностей парных значений, согласуется с нормальным законом распределения, а генеральная дисперсия di неизвестна, точные значения границ доверительного интервала, в котором с доверительной вероятностью P будет находиться среднее арифметическое значение генеральной совокупности
Для рассматриваемой задачи оно будет иметь вид:
По таблице критерия Стьюдента (Приложение 4) мы нашли, что для уровня значимости a = 0,05, числа степеней свободы k = n – 1 = 10 – 1 = 9 и двухсторонней критической области ta = 2,26. Стандартную ошибку среднего арифметического найдем по формуле:
Доверительный интервал для среднего арифметического прироста количества ударов за 10 с в генеральной совокупности равен:
1,35 уд. Следовательно, с доверительной вероятностью P = 0,95 можно утверждать, что в результате тренировки улучшение показателя скоростных качеств Для построения доверительного интервала необходимо выбрать масштаб. Выберем масштаб 1 уд ≡ 1 см.
Доверительный интервал для
Вариант 2: критерий непараметрический Примечание: В качестве примера возьмем приведенные в таблице 5.4 результаты измерения показателя скоростных качеств у спортсменов перед началом тренировок (они обозначены индексом В, были получены в результате измерений на I этапе деловой игры) и после двух месяцев тренировок (они обозначены индексом Г).
От выборок В и Г перейдем к выборке, составленной из разностей парных значений di = NiГ – NiВ и определим квадраты этих разностей. Данные занесем в расчетную таблицу 5.4.
Таблица 5.4 – Расчет квадратов парных разностей значений di2
Пользуясь таблицей 5.4, найдем среднее арифметическое парных разностей:
Далее рассчитаем сумму квадратов отклонений di от
Определим дисперсию для выборки di:
Далее необходимо выборку, составленную из разностей парных значений di, проверить на нормальность распределения. Выдвигаем гипотезы: – нулевую – H0: о том, что генеральная совокупность парных разностей di имеет нормальное распределение; – конкурирующую – H1: о том, что распределение генеральной совокупности парных разностей di отлично от нормального. Проверку проводим на уровне значимости a = 0,05. Для этого составим расчетную таблицу 5.3. Порядок заполнения таблицы 5.5 аналогичен порядку заполнения таблицы 5,3 и был описан в первом варианте выполнения V этапа.
Таблица 5.5 – Данные расчета критерия Шапиро и Уилка Wнабл для выборки, составленной из разностей парных значений di
По таблице 5.5 находим:
Наблюдаемое значение критерия Wнабл находим по формуле:
Проверим правильность выполнения расчетов критерия Шапиро и Уилка (Wнабл) его расчетом на ПЭВМ по программе «Статистика». Расчет критерия Шапиро и Уилка (Wнабл) на ПЭВМ позволил установить, что:
Далее по таблице критических значений критерия Шапиро и Уилка (Приложение 3) ищем Wкрит для n = 10. Находим, что Wкрит = 0,842. Сравним величины Wкрит и Wнабл. Делаем вывод: так как Wнабл (0,839) < Wкрит (0,842), должна быть принята конкурирующая гипотеза о распределении генеральной совокупности di, отличном от нормального. Поскольку выборки попарно зависимые, а распределение парных разностей отличается от нормального, для оценки эффективности применявшейся методики развития скоростных качеств следует использовать непараметрический U -критерий Уилкоксона.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.68.154 (0.008 с.) |

 и средним показателем скоростных качеств
и средним показателем скоростных качеств  , достигнутым после двух месяцев тренировок (
, достигнутым после двух месяцев тренировок ( );
); ).
).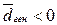 , в данном случае лишено здравого смысла, поэтому мы имеем дело с односторонней критической областью.
, в данном случае лишено здравого смысла, поэтому мы имеем дело с односторонней критической областью. уд.
уд. .
. , найдем из следующего двойного неравенства:
, найдем из следующего двойного неравенства:

 уд.
уд.

 8,65 уд.
8,65 уд.
 уд.
уд. по формуле:
по формуле: уд.2
уд.2 уд.2
уд.2 ;
; .
. .
. .
.


