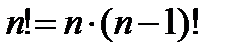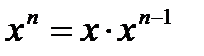Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Итерационные и арифметические циклы. Вложенные циклыСодержание книги
Поиск на нашем сайте Краткая теория Арифметические циклы Арифметические циклы предназначены для вычислений с заранее неизвестным количеством повторений итераций. Для данного вида циклов обычно используется оператор for, однако такую же функциональность можно реализовать и при помощи циклов do while и while. Рассмотрим примеры использования арифметических циклов. Например, необходимо вычислить значение факториала n!. Факториал числа n (обозначается n!, произносится эн факториа́л) – произведение всех натуральных чисел до n включительно: n! = 1*2*3*…*n. По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
#include <iostream> using namespace std; void main () { int n, nf = 1; cout << "Input number" << endl; cin >> n; for (int i = 1; i <= n; i ++) nf *= i; cout << "n! = " << nf; }
Однако шаг цикла может быть не только целым числом. При этом определенность количества итераций останется. Например, необходимо написать программу, печатающую таблицу значений функции Входными данными являются значения границы интервалов [x0,xn] и шаг dx. Все величины вещественные. Ввод и вывод осуществим при помощи функций библиотеки stdio.h.
#include <stdio.h> #include <math.h> void main () { float x0, xn, dx; printf ( "Input x0, xn, dx:\n" ); scanf ( "%f%f%f", & x0, & xn, & dx ); printf ( "+-----------+-----------+\n" ); printf ( "| x | y |\n" ); printf ( "+-----------+-----------+\n" ); for (float x = x0; x <= xn; x += dx ) { float y; if ( x > 1 ) y = pow ( x - 3, 3 )/ x; Else y = pow ( x, 3 ) -3 * x; printf ( "| %9.3f | %9.3f |\n", x, y ); } printf ( "+-----------+-----------+\n" ); }
Вложенные циклы Часто возникают ситуации, когда внутри одного цикла необходимо вычислить некоторое значение. И для его вычисления необходимо также организовать цикл. В этом случае применяется вложенность циклов. Вложенные циклы могут быть как арифметическими, так итерационными. При записи программ со структурой вложенных циклов необходимо обращать внимание на правильность размещения внешнего и внутреннего циклов. Одни постановки задач допускают смену мест внешнего и внутреннего циклов, а в других постановках такая система приводит к неправильным результатам. При записи программ со структурой вложенных циклов зона действия внутреннего цикла должна располагаться в зоне действия охватывающего цикла. Рассмотрим пример использования вложенных циклов. Составить программу вычисления значения функции
подсчитав первые 10 слагаемых. Для форматирования ввода-вывода с помощью манипуляторов setw и setprecision необходимо подключить библиотеку iomanip.
#include <iostream> #include <iomanip> #include <math.h> using namespace std; void main () { const int N = 10; float a, x, y, y0; cout << "Input a, x:" << endl; cin >> a >> x; y = 1; for (int n = 1; n <= N; n ++) { int nf = 1; for (int m = 1; m <= n; m ++) nf *= m; y += pow ( x * log ( a ), n )/ nf; } y0 = pow ( a, x ); cout << "Result of iterative calculation: " << setw ( 9 ) <<\ setprecision ( 5 ) << y << endl; cout << "Result of direct calculation: " << setw ( 9 ) <<\ setprecision ( 5 ) << y0 << endl; }
Итерационные циклы Для вычислений с заранее неизвестным количеством повторений итераций обычно используются операторы while и do while, однако C++ позволяет использовать для этих целей и оператор for. Циклический процесс, выполняющийся до достижения некоторого условия, называется итерационным. Учитывая неизвестность конечного числа шагов итерационного алгоритма, необходимо предусмотреть вариант зацикливания и сформулировать корректное условие для выхода из цикла. В самом простом случае, а также на этапе отладки алгоритма, достаточно поставить лимит числа шагов с выдачей сообщения в случае его исчерпания. В итерационных алгоритмах заданная погрешность используется для проверки модуля разности найденного приближенного и точного значений. В случае, когда точное значение неизвестно, допустимо оценивать разность между соседними итерациями. Значащими цифрами числа называются все цифры в его десятичной записи, кроме крайних левых и крайних правых нулей. При решении задач, как правило, нет необходимости хранить промежуточные итерации – достаточно получения окончательного результата и (в итерационных алгоритмах) числа шагов, проделанных для достижения условия – для оценки скорости сходимости алгоритма. Часто в задачах для вычисления очередного слагаемого удобно рекуррентно использовать предыдущее слагаемое, а не организовывать дополнительный (внутренний) цикл. Рассмотрим пример использования итерационных циклов. Возьмем ту же задачу, что и для вложенных циклов, но несколько модифицируем ее. Составить программу вычисления значения функции
с погрешностью e = 10-3 и напечатать для контроля значения функции, определяемые выражениями в правой и левой частях равенства. Сколько итераций надо выполнить, чтобы для заданной погрешности e было справедливо соотношение
Решение. Вычисление факториала можно организовать рекуррентно, т.е. умножая каждый раз некоторую переменную на значение счетчика n. Вычисление рекуррентных значений можно осуществить на основе следующей формулы:
Поэтому нет необходимости вычислять факториал каждый раз заново, достаточно домножить предыдущее значение на значение переменной n. Аналогичным образом можно вычислить и операцию возведения в степень (значение (x*log(a))n в примере). Для этого используется формула:
Здесь тоже нет необходимости вычислять степень числа каждый раз заново, достаточно домножить предыдущее значение на x.
#include <iostream> #include <iomanip> #include <math.h> using namespace std; void main () { const float eps = 0.001f; float a, x, xn = 1, y, y0; unsigned int n = 1, nf = 1; cout << "Input a, x:" << endl; cin >> a >> x; y = 1; do { nf *= n; xn *= x * log ( a ); y0 = y; y += xn / nf; n ++; } while ( abs ( y - y0 ) > eps ); y0 = pow ( a, x ); cout << "Result of iterative calculation: " << setw ( 9 ) <<\ setprecision ( 5 ) << y << endl; cout << "Result of direct calculation: " << setw ( 9 ) <<\ setprecision ( 5 ) << y0 << endl; cout << "Number of iterations: " << setw ( 5 ) << n << endl; }
Замечание. Поскольку значение факториала растет чрезвычайно быстро (12! = 479 001 600, а 13! = 6 227 020 800), значения свыше 12! уже не помещаются в переменную типа int. Поэтому результаты с количеством итераций больше 12 будут содержать значительные погрешности. Это происходит из-за явления оборачивания, суть которого можно кратко выразить такими соотношениями: 0xFFFF + 0x0001 = 0x0000 0x0000 – 0x0001 = 0xFFFF Т.е если последовательно увеличивать содержимое какой-либо целочисленной беззнаковой переменной, то, достигнув верхнего возможного предела, число превысит эту границу, станет равным нулю и продолжит нарастать в области малых положительных чисел (1, 2, 3, и т.д.). Точно так же, если последовательно уменьшать некоторое число, то оно, достигнув нуля, перейдет в область больших положительных. Это же касается и чисел со знаком: достигнув верхнего положительного предела, число превысит эту границу, станет равным минимальному отрицательному числу, а если последовательно уменьшать некоторое отрицательное число, то оно, достигнув минимального значения, оно перейдет в область больших положительных. Увидеть явление оборачивания можно на следующем примере. 2147483647 +1 = -2147483648 -1 =
|
||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 981; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |

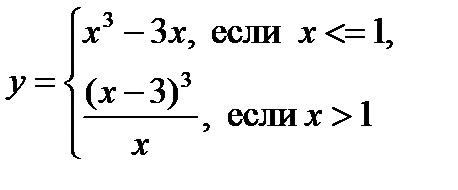 на интервале [0.5, 1.5] с шагом 0.1.
на интервале [0.5, 1.5] с шагом 0.1.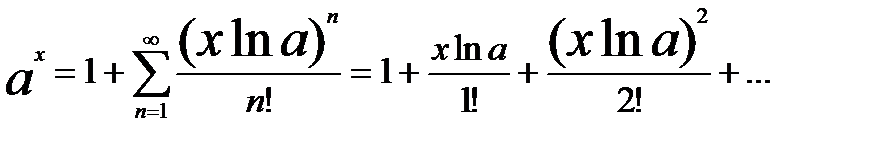
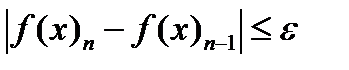 ?
?