
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило фаз Гиббса для дисперсных системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В физ. химии правило фаз Гиббса имело вид F = к+ф+2, где под 2 понимают термодинамически интенсивные переменные P,T, т.е. таким образом определяется число степеней свободы или вариантность системы. F – число независимых переменных, которые можно изменять в некоторых пределах так, чтобы число и природа фаз оставались прежними. Наименьшее число переменных описывает состояние системы. Для газа F=2 Рассмотрим теперь трехкомпонентную гетерогенную систему бензол-вода-ПАВ. Здесь F=3-2=1, P,T – const, 1 – количество ПАВ. Но, если 1. цилиндр 2. противень
Как распределится ПАВ в этих случаях? S1<S2; Sуд1<Sуд2; 1. mпПАВ,ц<mпПАВ,пр; 2. cvПАВ,ц>cvПАВ,пр т.е. изменеие Sуд или Д привело к изменению равновесия в системе, т.е. система получила дополнительную степень свободы. Отсюда Д (Sуд) является самостоятельным термодинамическим параметром системы, изменение которого вызывает соответствующие изменения других равновесных свойств системы. Sуд является интенсивным признаком системы. Ее можно характеризовать как количество поверхности, приходящимся на 1 обьема. Отсюда: правило фаз Гиббса для дисперсных систем может быть записано: F=к+ф+3, где под 3 понимают P,T,S. 1.7 Молекулярно-кинетические свойства свободно-дисперсных систем. В 1827г. Английский ботаник Роберт Броун исследуя споры папоротника в воде обратил внимание на их хаотические движения, которые зависели от их размера и температуры. Только в конце 19в. Гуи и Экспер связали это с тепловым движением молекул. Фактически это открытие доказывало существование атомов и молекул. Экспер попытался количественно описать эти движения, используя уравнения кинетической энергии частиц Однако вычисления давали значения перемещений в 1000 раз больших, (4000 мкм/с вместо 4мкм/с) чем экспериментальные. Это можно было объяснить используя только законы статической физики. В 1 сек. частицы испытывают до 1020 толчков и перемещение частиц является источником их результирующего воздействия.
Учитывая равновероятность отклонения от осей «x» и «y» (∟45˚) имеем
Они установили также количественную связь между кв. средним сдвигом 1. С1 < С2. Хаотичность броуновского движения приводит к равной вероятности перехода частиц из 1 в 2, т.е. половина частиц переместится вправо, половина влево.
Градиент конц. (с1 - с2) может быть выражен:
Из первого закона Фика Приравняем: Уравнение Эйнштейна для диффузии:
гдеВ – коэффициент трения;
т.е. частицы перемещаются тем сильнее чем выше Т, τ и меньше η и r. Экспериментально это уравнение было доказано Сведбергом (1909), Перреном (1910), Бойлем (1909), Милликеном (1910). Сведберг – измерил сдвиг частиц коллоидного Ag от τ и η, что совпало с уравнением Перрен – впервые экспериментально на системе гуммигут-H2O определил NA Бойль – на табачном дыме, используя закон Энштейна-Смоулховского, определил заряд частиц аэрозоля. Милликен – использовал систему масляного тумана, экспериментально определил заряд «e» очень точно. ВЫВОДЫ: Доказательство справедливости закона Эйнштейна-Смоулковского для коллоидных систем привела к фундаментальным выводам о применимости к истинным коллоидным системам законов молекулярно-кинетической теории, законов связанных с энтропией, т.е. коллоидные системы обладают свойствами гетерогенно-дисперсных систем и истинных растворов. Поверхностное натяжение Почему по водной поверхности бегают пауки? Почему металлическая игла удерживается на водной поверхности? Почему англичане еще в XVII – XVIII вв. выливали в бушующее море тюлений или китовый жир? Как норвежские рыбаки определяли место косяка сельди? Еще раз посмотрим на энергетическое положение атома внутри тела и на его поверхности.
Б.(на поверхности) Fрез≠0 и направлена внутрь тела
Втягивая поверхностные атомы внутрь, тело как бы стремится уменьшить свою поверхность. На поверхности возникает напряжение, вызванное наличием избыточной энергии из-за нескомпенсированности энергии поверхностных атомов. 1. Избыточная поверхностная энергия приходящаяся на единицу площади поверхности получила название поверхностного натяжения (σ) Физическая природа σ в нескомпенсированности поля межмолекулярных сил на межфазных поверхностях. 2. Его можно также трактовать как силу, действующую тангенциально поверхности (вдоль нее) и препятствующую увеличению поверхности. Опыт Дюпре с мыльной пеной. 3. σ – можно также рассматривать как работу, затраченную на разрыв межатомных или межмолекулярных связей, т.е. это работа образования единицы поверхности. На σ влияют T, q, добавки ПАВ. [σ]=Дж/м2; Нм/м2=Н/м. В СГС: дин/см; 1 Н/м=1000 дин/см Чем сильнее межмолекулярные связи в веществе, тем больше σ на его межфазной поверхности. Отсюда: H2O → σ=0,0721 Дж/м2
 C2H5OH → 0,0221 C2H5OH → 0,0221
Fe → 4,0 W → 6,8 Алмаз → 11,4 – макс. знач.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.57 (0.009 с.) |

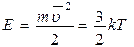 , k – const Больцмана.
, k – const Больцмана. Теоретически обосновали броуновское движение Эйнштейн (1905) и Смолуховский (1906) – независимо друг от друга. Оба они приняли представление о среднем сдвиге частицы в двух координатах «x» и «y» как их проекции движения на плоскости.
Теоретически обосновали броуновское движение Эйнштейн (1905) и Смолуховский (1906) – независимо друг от друга. Оба они приняли представление о среднем сдвиге частицы в двух координатах «x» и «y» как их проекции движения на плоскости. ,
,  или
или  ;
;
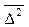 и коэффициентом диффузии Д.
и коэффициентом диффузии Д.
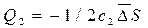

 , подставив
, подставив

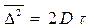
 ,
, - закон Стокса
- закон Стокса - закон Эйнштейна-Смолуховского,
- закон Эйнштейна-Смолуховского, А.(внутри)
А.(внутри) Fрез=0
Fрез=0




