
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема.3. Вибіркове спостереженняСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Питання для обговорення на практичному занятті і самостійної підготовки: 1. Сутність та види вибіркового спостереження при оцінці якості 2. Вибіркова оцінка параметрів якості генеральної сукупності. 3. Зміст і техніка обчислення вибіркових параметрів якості Література: 1; 2; 7. В практичній діяльності проведення спостереження, яке б охоплювало всі елементи сукупності, є часто неможливим. Причини цьому можуть бути різними: труднощі із отриманням потрібної інформації по всім одиницям сукупності; властивості об'єкта дослідження; витрати, пов'язані із дослідженням кожної одиниці сукупності тощо. Тому для збору необхідної інформації застосовують вибіркове спостереження. Вибірковим називається вид несуцільного спостереження, за характеристиками відібраної частини одиниць якого судять про всю сукупність. Сукупність, з якої відбираються елементи для обстеження, називають генеральною, а сукупність, яку безпосередньо обстежують, вибірковою. Оскільки вибіркова сукупність не точно відтворює структуру генеральної, то вибіркові характеристики не збігаються з характеристиками генеральної сукупності. Розбіжності між ними називають похибками репрезентативності. За причинами виникнення ці похибки поділяються на систематичні (тенденційні) та випадкові. Систематичні похибки виникають за умови, що під час формування вибіркової сукупності порушується принцип випадковості вибору (упереджений вибір елементів, недосконала основа вибірки тощо). Випадкові похибки це такі, які неминуче виникають і при дотриманні принципу випадковості відбору. Вони не носять тенденційний характер і не ведуть до зміщення узагальнюючих показників генеральної сукупності. Головне завдання при організації вибіркового обстеження полягає в запобіганні виникнення систематичних похибок. Що стосується випадкових похибок, то їх уникнути неможливо, проте на основі теорії вибіркового методу можна визначити їхній розмір і по можливості регулювати. Якщо принцип випадковості відбору не порушувався, то середня похибка вибірки (m) визначається за формулами:
З допомогою середньої похибки вибірки, межі довірчого інтервалу для генеральної середньої або частки визначаються з імовірністю лише 0,683. Щоб підвищити імовірність твердження про межі, в які потраплять генеральні характеристики, обчислюють граничну похибку вибірки (
де t –коефіцієнт довіри, що підвищує імовірність твердження про потрапляння генеральних узагальнюючих показників до розрахованих довірчих меж. Щоб добитися довірчої ймовірності = 0,954, середню похибку вибірки подвоюють, тобто t = 2; для довірчої ймовірності = 0,997 довірче число t =3.
Довірчий інтервал записується за формулами: - для середнього:
- для частки:
Приклад 3. Проведено вибіркове дослідження 25 пакетів з чаєм. Визначено вагу чайного листа, що знаходиться в кожному пакеті. З ймовірністю 0,997 потрібно визначити вагу чайного листа у продукції. Результати спостереження наведені в табл. 3.1. Таблиця 3.1. Результати вибіркового спостереження ваги чайного листа у пакетах
Вибіркова середня вага чаю у пакетику становить:
На основі даних визначаємо дисперсію вибіркових даних:
Для визначення меж ваги чаю у генеральній сукупності знаходимо середню помилку вибірки:
Для ймовірності 0,997 визначаємо граничну помилку вибірки. Оскільки ймовірність дорівнює 0,997, то коефіцієнт кратності помилки (коефіцієнт довіри) дорівнює 3.
Таким чином, середня вага чаю у пакетику для всієї виготовленої за даних умов виробництва продукції, знаходиться у межах:
тобто, від 99,708гр. до 100,404гр. Приклад 4. Для визначення ставлення покупців до рівня якості обслуговування у магазині потрібно провести вибіркове дослідження. Покупці оцінюють рівень обслуговування за 7 бальною шкалою (1 дуже погано, 7 дуже добре). З рівнем ймовірності 0,954 потрібно визначити обсяг вибірки для випадку, щоб гранична помилка не перевищувала 0,25 бали. Розв'язок. За результатами попереднього дослідження відомо, що тандартне відхилення оцінок покупців складає 1,45 бали. Тому
Таким чином для отримання репрезентативних даних із заданою точністю, потрібно провести анкетування серед 135 відвідувачів магазину.
Завдання для виконання на практичному занятті і самостійної підготовки Завдання 1. Хімічний аналіз 10 партій молока дав такі показники кислотності (у градусах Тернера): 18; 21; 17; 19; 20; 23;16; 22; 24; 21. На основі вищенаведених даних визначте: - середній рівень кислотності молока та граничну похибку вибірки для середньої з ймовірністю 0,954; - частку молока, що відповідає стандартові (не більше 21°), та похибку вибірки для частки з ймовірністю 0,954; - скільки пар тій молока необхідно перевірити, щоб похибка вибірки для частки нестандартного молока зменшилась у 2 рази? Завдання 2. З метою перевірки якості овочевих консервів (у склотарі) методом серійної вибірки з 200 ящиків по 20 банок } кожному відібрано 4. За даними перевірки має місце не якісна герметизація банок:
На основі вищенаведених даних визначте: а) частку банок з неякісною герметизацією та довірчий інтервал: б) чи можна стверджувати, що частка банок з неякісною гермети Завдання 3. Вперше організується одномоментне спостереження за ефективністю використання 50 одиниць виробничого устаткування. Скільки спостережень необхідно провести, щоб похибка вибірки для частки устаткування, що не працює, з ймовірністю 0,954 не перевищила 2 %? За умови, що спостереження триватиме 10 днів, скільки спостережень необхідно зробити щоденно за кожною одиницею устаткування? Завдання 4. За даними 5 %-ого вибіркового обстеження, верстати за терміном служби розподіляються так:
На основі вищенаведених даних визначте: а) середній термін служби верстатів та довірчий інтервал для се б) з тією ж ймовірністю визначте граничну похибку та довірчий Завдання 5. З метою визначення зольності вугілля, яке надійшло на електростанцію з різних вагонів, узято 100 проб. Результати аналізу такі:
На основі вищенаведених даних визначте: а) середню зольність вугілля та довірчий інтервал для середньої з ймовірністю 0,954; б) з тією ж ймовірністю визначте довірчий інтервал частки вугілля, зольність якого менша 16 %. Тема.4. Статистична перевірка гіпотез Питання для обговорення на практичному занятті і самостійної підготовки: 1. Статистична гіпотеза. Основні поняття і принципи перевірки 2. Перевірка гіпотез про рівність дисперсій 3. Перевірка гіпотез про рівність середніх 4. Перевірка гіпотез про частку сукупності Література: 1; 2; 7. Статистична гіпотеза - це певне припущення щодо властивостей генеральної сукупності, яке перевіряють за даними вибіркового спостереження. Найчастіше це гіпотеза про характеристики ознаки якості та про параметри відомого розподілу. Гіпотеза, яку належить перевірити, формулюється як відсутність розбіжностей між параметром генеральної сукупності С і заданою величиною а. Ця висунута гіпотеза має назву нульової і записується: H 0: С = a. Кожній нульовій гіпотезі Но висувається конкуруюча (альтернативна) гіпотеза Н1(Н0), яка вступає у протиріччя з Н0. Залежно від виду і вагомості відхилень вона може бути сформульована як: Н1 :С > а, Н1:С<а, Н1: С≠ а. В результаті перевірки гіпотези можуть бути припущені помилки 2 видів. Помилка 1 виду полягає в тому, що буде відкинута правильна гіпотеза H 0. Ймовірність помилки 1 виду називають рівнем значущості (істинності) і позначають Помилка 2 виду полягає в тому, що буде прийнята невірна гіпотеза, і її ймовірність позначається як р. Тобто прийнята Н0, коли насправді вірною є альтернативна Н1. Правило, за яким статистична гіпотеза Н0 відхиляється або не відхиляється, називають статистичним критерієм. В якості його виступає певна випадкова величина К, яка застосовується для перевірки гіпотези, закон розподілу якої є відомим. Коли виникає необхідність порівняння двох методів вимірювання, точності роботи двох видів обладнання, однорідності двох сукупностей тощо, доцільно скористатися перевіркою гіпотези про рівність двох дисперсій генеральних сукупностей. Нехай з двох генеральних сукупностей отримані вибірки обсягом n1 і n2, для кожної з яких визначена скоригована (незміщена) вибіркова дисперсія
при рівні значущості Для цього погрібно знайти спостережуване значення критерію як відношення більшої дисперсії до меншої:
Далі, за таблицею критичних точок розподілу Фішера- Снедекора для рівня значущості якщо Fспост>Fкр - тоді відкидаємо Н0,; якщо Fспост<Fкр - тоді приймаємо Н0.. Приклад 5. На підприємстві протягом місяця в середньому створювалося 38 невідповідностей на 1000 виробів. Після дій по вдосконаленню виробництва на 500 виробів було визначено 12 невідповідностей. Постає питання, чи можливо із рівнем значущості 0,01 стверджувати, що дії були ефективними? Розв'язок: Для встановлення ефективності застосованих дій скористаємося перевіркою гіпотези про рівність двох часток. Частка невідповідних виробів до дій по вдосконаленню виробництва становить р] =38/1000-0,038. Частка невідповідностей після вдосконалення дорівнює р2 = 12/500 = 0,024. Таким чином, розрахункове значення критерію становить:
Значення t-критерію перевірки значущості
Двостороння критична точка дорівнює
З таблиці функції Лапласа знаходимо критичне значення критерію Z = 2,34. Оскільки розрахункове значення критерію менше за критичне, то із рівнем значущості 0,01 можливо стверджувати, що немає підстав відкинути нульову гіпотезу, тобто вжиті заходи в дійсності не підвищили ефективність виробництва. Приклад 6. На основі хронометражу часу, потрібного на встановлення певного елементу у виріб різними працівниками, встановлено, що дисперсія складає 2 хв. Результати хронометражу часу роботи нового наступні:
Чи можемо ми вважати, що за рівня значущості α = 0,05 новий робітник працює ритмічно? Розв'язок. Потрібно перевірити гіпотезу, що дисперсія часу, який витрачає на зборку новий робітник, істотно не відрізняється від дисперсії часу інших робітників (гіпотетичної дисперсії).Визначаємо дисперсію витрат часу нового робітника. Середній час за формулою середньої арифметичної зваженої дорівнює:
Дисперсія становить:
Знаходимо розрахункове значення критерію χ-квадрат:
Оскільки альтернативна гіпотеза має вид рівності, то потрібно встановити ліву і праву критичні точки. В нашому випадку для 19 ступенів свободи ліва критична точка χ2лів.кр .=8,91 і права критична точка χ2прав..кр .=32,9. Так як спостережуване значення перевищує праву критичну точку, то є підстави відкинути гіпотезу про рівність вибіркової дисперсії гіпотетичній, і зробити висновок, що новий робітник працює неритмічно. Приклад 7. В середньому вимикачі даного типу розраховані на2000 вмикань при σ =100. В результаті вибіркової перевірки якості 50 вимикачів даного заводу-виробника встановлено, що середнє число вмикань склало 2080. Необхідно встановити чи суттєво відрізняється якість вимикачів даного заводу-виробника. Розв'язок. Для порівняння вибіркової середньої ознаки якості з генеральною середньою ознакою розраховується статистика
Оскільки
Завдання для виконання на практичному занятті і самостійної підготовки Завдання 1. Було визначено середнє квадратичне відхилення певного процесу на рівні 2,55 грам. Після певних коригуючих дій було зроблено вибірку у 10 одиниць продукту і встановлено, що середнє квадратичне відхилення дорівнює 3,3 грам. При рівні значущості ά= 0,05 перевірити гіпотезу про те, що рівень варіабельності процесу не змінився. Завдання 2. Зразки двох різних видів пластика було перевірено на силу розриву. Одержано такі результати:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 942; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.141.201 (0.014 с.) |





 ).
). ,
,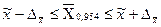
 -
- 
 +
+ 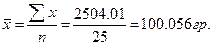





 .
. та
та  відповідно. Потрібно порівняти дисперсії цих сукупностей, тобто перевірити гіпотезу:
відповідно. Потрібно порівняти дисперсії цих сукупностей, тобто перевірити гіпотезу:







 )2
)2


 , можна вважати, що якість вимикачів даного заводу-виробника суттєво вище встановленої для вимикачів даного типу.
, можна вважати, що якість вимикачів даного заводу-виробника суттєво вище встановленої для вимикачів даного типу.


