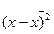Тема. 2. Варіація ознак якості та її вимір

Питання для обговорення на практичному занятті і самостійної підготовки:

1. Варіація ознаки, її сутність
2. Статистичні показники варіації ознак якості
3. Зміст і техніка обчислення показників варіації ознак якості

Література: 1;7.

Надзвичайно важливою характеристикою будь-якого явища чи процесу є його варіація.

Варіація це природне розсіювання індивідуальних значень ознаки. Варіація існує в усіх явищах і процесах. Вона виникає внаслі­док дії численних причин, які або підсилюють, або зменшують варіа­цію, її неможливо позбутися, оскільки варіабельність є внутрішньо притаманною складовою всього існуючого, але її можливо оцінювати і контролювати шляхом здійснення певних дій. Варіація знаходить свій прояв лише у масових явищах, і тому вивчається статистикою, як наукою про масові явища та процеси. Варіація ознак, які вивчаються, є одним з основних статистичних понять і відіграє надзвичайно вели­ку роль в характеристиці об'єкта дослідження. В статистиці існує ряд показників, за допомогою яких можливо надати кількісного виразу мірі варіації певної ознаки Ці показники узагальнюють відхилення індивідуальних значень від середнього значення досліджуваної озна­ки, тобто є середніми з індивідуальних відхилень.

Найпростішим показником, який характеризує варіацію ознак є розмах варіації (R), який являє собою різницю між максимальним (X _max) і мінімальним ( X _min ) значенням ознаки:

R= X _max – X _min

Він показує, в яких межах варіює ознака. Але як міра варіації цей показник не завжди надійний, оскільки залежить від випадкових ко­ливань крайніх значень ознаки.

Середня із абсолютних відхилень називається середнім лінійним відхиленням (d), яке, аналогічно середнім величинам, буває простим і зваженим. Просте середнє лінійне відхилення використовується в тих випадках, коли розрахунок ведеться по незгрупованим даним:

Середнє лінійне відхилення зважене використовується в тих ви­падках, коли дані, по яких ведеться розрахунок, згруповані:

де f - частота повторюваності ознаки.

Середня із квадратів відхилень називається дисперсією (о²) і роз­раховується за наступною формулою:

проста

 

зважена

Для того, щоб дати характеристику варіації в тих же одиницях виміру, що і досліджувана ознака, потрібно з дисперсії добути квад­ратний корінь. Отриманий в результаті показник має назву середньо­го квадратичного відхилення і розраховується як:

Середнє квадратичне відхилення ще має назву стандартне відхилення і показує, на скільки одиниць в середньому індивідуальні зна­чення ознаки відхиляються від середнього значення.

Для альтернативної ознаки, коли р - частка елементів з певною ознакою у сукупності, дисперсія визначається як:

Коефіцієнт варіації (квадратичний) являє собою виражене у відсотках відношення середньоквадратичного відхилення до середньої арифметичної, використовується для порівняльної оцінки ступеню варіації одиниць сукупності та характеристики однорідності сукупності за ознакою якості.

Сукупність вважається якісно однорідною, якщо коефіцієнт варіації не перевищує 33%.

 

Приклад 2. Виробник батарей формату АА досліджує час роботи батарейок. Проведено 10 замірів тривалості роботи, результати яких наведено нижче (у годинах):

Таблиця 2.1. Результати замірів тривалості роботи батарейок

 

 

№
Час роботи	25,.5	26,8	24,2	25,0	27,3	26,1	23,2	28,4	27,8	25,7

Керівництву потрібно знати варіацію часу роботи батарейок.

Розв 'язок. За цими даними розмах варіації становить:

R= X _max – X _min=28,4-23,2=5,2 год

Для знаходження середнього квадратичного відхилення спочатку потрібно визначити середній час роботи:

 

Далі визначаємо середнє квадратичне відхилення:

Таблиця 2.2. Розрахунки для визначення варіації тривалості роботи батарейок

 

№ з/п	x
	25,5	-0,50	0,25
	26,8	0,80	0,64
	24,2	-1,80	3,24
	25,0	-1,00	^Г 1,00
	27,3	1,30	1,69
	26,1	0,10	0,01
	23,2	-2,80	7,84
	28,4	2,40	5,76
	27,8	1,80	3,24
	25,7	-0,30	0,09
Разом	260,0	Х	23,76

 

Підставивши суму квадратів відхилень індивідуальних значень ознаки від середньої величини у формулу середнього квадратичного відхилення, отримаємо:

Отже, в середньому час роботи батарейки відрізняється від серед­нього часу роботи у 26 годин на 1,54 години.

 

Завдання для виконання на практичному занятті і самостійної підготовки

Завдання 1. Дві моделі кросівок перевіряють на тривалість зносу. По моделях отримано наступні дані про кількість годин ви­користання до появи першого значного дефекту:

 

 

Марка А	Марка Б

 

На основі вищенаведених даних визначити:

1. Яка модель взуття має довший час використання.

2. Який виробник має систему якості, що забезпечує вищу відпо­відність вимогам.

Завдання 2. Керівник наймає секретарку. Яку з двох кандидаток він повинен обрати, якщо на 6 сторінках перша зробила від­повідно 5, 6, 2, 1, 2, 0 помилок, а друга - 3, 4, 5, 3, 4, 5?

Завдання 3. До магазина протягом години зайшло відповідно 34, 45, 23, 34, 26, 32, 31, 41 відвідувача. На скільки відрізняєть­ся в середньому кількість відвідувачів щогодини?

Завдання 4. Керівник підприємства доручив дослідити варіабель­ність втрат організації через відсутність працівників з різних причин. З відділу кадрів отримано наступні дані:

Відсутність працівника, днів на рік	Кількість випадків
0-10
11-21
22-32
33-43
44-54
55-65
65 і більше
Всього

Завдання 5. На підприємстві виготовлена пробна партія деталей з 20 одиниць. Результати спостережень:

№з/п	Розмір деталі (мм)	Кількість деталей
	34,8
	34,9
	35,0
	35,1
	35,3
Всього	-

На основі цих даних визначити дисперсію і середнє квадратичне відхилення виготовлених деталей.

Завдання 6. На хімічному виробництві використовується два різних каталізатори реакцій. Результати виходу речовини при використанні кожного каталізатора наведені у наступній таблиці:

№ спостереження	Каталізатор № 1	Каталізатор № 2
	91,50	89,19
	94,18	90,95
	92,18	90,46
	95,39	93,21
	91,79	97,19
	89,07	97,04
	94,72	91,07
	89,21	92,75
Середня	92,255	92,733

 

Використовуючи результати, наведені в табл. 4, визначте середнє квадратичне відхилення і коефіцієнт варіації виходу речовини після реакції з кожним каталізатором.