
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахуємо показники варіації.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
До абсолютних показників варіації відносяться розмах варіації, середнє лінійне відхилення, дисперсія, середнє квадратичне відхилення, квартильное відхилення, інше. Розмах варіації є різницею між максимальним і мінімальним значеннями ознаки: R = Xmax - Xmin. R = 540-375 = 165. Даний показник зручний своєю простотою, але залежить від крайніх значень. Тому область застосування його обмежена. Більшість показників варіації заснована на розгляді відхилень значень ознаки окремих одиниць від середньої арифметичної. До таких показників відносять середнє лінійне відхилення, дисперсію, середнє квадратичне відхилення. Середнє лінійне відхилення для незгрупованих даних розраховується за формулою:
для згрупованих даних за формулою:
.
Дисперсія - це середнє з квадратів відхилень варіантів значень ознаки від їх середньої величини. Для згрупованих даних дисперсія розраховується за наступною формулою:
Але для перевірки правила додавання дисперсій ще потрібно розрахувати дисперсію за незгрупованими даними. Для розрахунків використовується формула дисперсії простої з використанням середнього значення, розрахованого за незгрупованими даними (25 значень у прикладі):
(375-469,88)2 + (390-469,88)2 + (403-469,88)2 + (412-469,88)2 + (437-469,88)2 + (446-469,88)2 + (449-469,88)2 + (454-469,88)2 + (457-469,88)2 + (464-469,88)2 + (467-469,88)2 + (472-469,88)2 + (472-469,88)2 + (483-469,88)2 + (485-469,88)2 + (485-469,88)2 + (488-469,88)2 + (489-469,88)2 + (496-469,88)2 + (504-469,88)2 + (512-469,88)2 + (517-469,88)2 + (526-469,88)2 + (526-469,88)2 + (538-469,88)2 / 25 =1756,1. Середнє квадратичне відхилення є коренем квадратний з дисперсії і визначається для варіаційного ряду за формулою:
Для порівнянь варіацій різних ознак використовують відносний коефіцієнт варіації. Це виражене у відсотках відношення середнього квадратичного відхилення до середньої арифметичної:
Сукупність вважається кількісно однорідною, якщо коефіцієнт варіації не перевищує 33%. V = 40,56/469,4 *100 = 8,6% < 33%. Згідно проведеному аналізу дана сукупність якісно однорідна.
Визначимо відносні характеристики варіації, показники асиметрії. Для порівнянь варіацій різних ознак використовують відносний коефіцієнт варіації. Це виражене у відсотках відношення середнього квадратичного відхилення до середньої арифметичної:
Сукупність вважається кількісно однорідною, якщо коефіцієнт варіації не перевищує 33%. V = 40,56/469,4 *100 = 8,6%. Згідно проведеному аналізу дана сукупність якісно не однорідна. Коефіцієнт осциляції: КR = R / х =165 / 469,4 = 0,35 або 35%. Відносне лінійне відхилення визначається як відношення середнього лінійного відхилення до середнього значення ознаки. Кd = d / Емпірична крива дозволяє заздалегідь припустити форму теоретичної кривої розподілу, що характеризує функціональний зв'язок між зміною варіюючої ознаки і зміною частот.
Рис. 1.5. Емпірична крива розподілу домогосподарств за розміром місячного доходу Те, що сукупність не має чітко визначеної асиметрії виходить із недотримання умов: Мо>Ме>х (лівостороння), Мо<Ме<х (правостороння). Тоді як в прикладі: 469, 3<471,9>469,4 Коефіцієнт асиметрії: As = (Х-Ме)/s = (469,4-471,9) / 40,56 = - 0,06. - від`ємний, тому вказує на нечітко виражену лівосторонню асиметрію.
Визначимо міжгрупову, внутрішньогрупову і загальну дисперсії, коефіцієнт детерміації. Варіація ознаки обумовлена різними чинниками, деякі з яких можна виділити, якщо статистичну сукупність розділити на групи за якою-небудь ознакою. Коли сукупність розчленована на групи по одному чиннику, вивчення варіації досягається за допомогою числення і аналізу трьох видів дисперсій: загальної, міжгрупової і внутрішньогрупової. Таблиця 1.2 Розподіл доходу господарств
У нашому прикладі дані групуються за розміром доходу домогосподарств. Результативна ознака варіює як під впливом систематичного чинника, так і інших неврахованих випадкових чинників (внутрішньогрупова варіація). група 1: група 2: група 3: група 4: група 5:
Розрахуємо внутрішньогрупові дисперсії за формулою:
Внутрішньогрупові дисперсії показують варіації сум доходу в кожній групі, викликані всіма можливими чинниками. Розрахуємо середню з внутрішньогрупових дисперсій:
Середня з внутрішньогрупових дисперсій відображає варіацію суми доходу, обумовлену всіма чинниками, окрім розміру доходу, але в середньому по всій сукупності. Обчислимо міжгрупову дисперсію.
Міжгрупова дисперсія характеризує систематичну варіацію результативного порядку, обумовлену впливом ознаки - чинника, покладеного в підставу угрупування. Обчислимо загальну дисперсію, згідно правилу складання дисперсій, за наступною формулою:
Загальна дисперсія вимірює варіацію ознаки по всій сукупності під впливом всіх чинників, що зумовили цю варіацію. Чим більше частка міжгрупової дисперсії в загальній дисперсії, тим сильніше вплив группировочного ознаки. Для характеристики даного зв'язку застосовують емпіричний коефіцієнт детермінації:
У нашому прикладі:
Емпіричне кореляційне відношення:
Згідно якісній оцінці тісноти зв'язку Чеддока, в нашому прикладі існує дуже тісний зв'язок між сумою місячного доходу домогосподарства і розміром доходу як групувальної ознаки.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 ,
, .
.
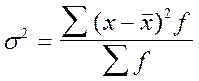 .
.

 .
.
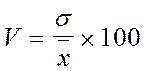

 =33,5 / 469,4 = 0,071 або 7,1%.
=33,5 / 469,4 = 0,071 або 7,1%.
 = 1168 / 3 = 389,3;
= 1168 / 3 = 389,3; = 849 / 2 = 424,5;
= 849 / 2 = 424,5; = 3681 / 8 = 460,1
= 3681 / 8 = 460,1 = 3430 / 7 = 490;
= 3430 / 7 = 490;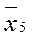 = 2619 / 5 = 523,8;
= 2619 / 5 = 523,8; .
. 1 = ((375-389,3)2+(390-389,3)2+(403-389,3)2/3=392,67/3=130,89;
1 = ((375-389,3)2+(390-389,3)2+(403-389,3)2/3=392,67/3=130,89;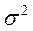 4 = ((483-490)2 + (485-490)2 + (485-490)2 + (488-490)2 + (489-490)2+ (496-490)2 + (504-490)2) = 336/7 = 48.
4 = ((483-490)2 + (485-490)2 + (485-490)2 + (488-490)2 + (489-490)2+ (496-490)2 + (504-490)2) = 336/7 = 48. .
. (130,89х3 + 156,25х2 + 91,26х8 + 48х7 + 79,36х5)/25 = 86,72.
(130,89х3 + 156,25х2 + 91,26х8 + 48х7 + 79,36х5)/25 = 86,72. .
. ((389,3-469,9)2 +(424,5-469,9)2 +(460,1-469,9)2 +(490-469,9)2 +(523,8-469,9)2) / 25 = 1669,35.
((389,3-469,9)2 +(424,5-469,9)2 +(460,1-469,9)2 +(490-469,9)2 +(523,8-469,9)2) / 25 = 1669,35. = 86,72 + 1669,35 = 1756,1.
= 86,72 + 1669,35 = 1756,1. .
. 1669,35/1756,1=0,951.
1669,35/1756,1=0,951. .
.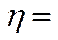 0,975.
0,975.


