
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дослідження асиметрії розподілуСодержание книги
Поиск на нашем сайте
Головне завдання аналізу варіаційних рядів – визначення дійсної закономірності розподілу шляхом виключення другорядних, випадкових для даного розподілу факторів. Під кривою розподілу розуміється графічне зображення у вигляді безперервної лінії зміни частот у варіаціному ряду на основі полігону або гістограми. Для однорідної сукупності, як правило, характерним є одновершинний розподіл. Багатовершинність свідчить про неоднорідність вивчаємої сукупності.
Відносний показник – коефіцієнт асиметрії As:
Коефіцієнт асиметрії може бути позитивним чи від’ємним. У першому випадку мова йде про правосторонню асиметрію (рис.1), а в другому – про лівосторонню (рис. 2). У симетричному розподілі Аs = 0. Коефіцієнт асиметрії коливається в межах від -3 до +3.
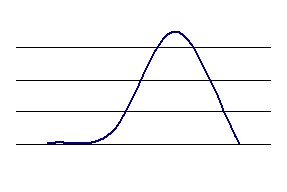
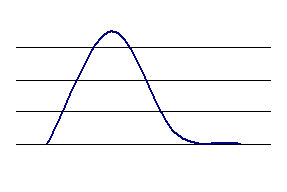
Рис. 1 Правостороння асиметрія Рис. 2 Лівостороння асиметрія
У разі чіткої асиметрії варіаційного ряду середнє значення ознаки має доповнюватися модою і медіаною. В асиметричному розподілі між середньою арифметичною, медіаною і модою існують певні розбіжності. У разі правосторонньої асиметрії: У випадку недотримання ні однієї з вищезгаданих умов висновок з асиметричності робиться, зважаючи зі знаку коефіцієнту асиметрії: якщо Аs > 0, - слід вважати, що сукупність має слабко виражену правосторонню асиметрію, якщо Аs < 0 – слабко виражену лівосторонню асиметрію.
5. Визначення ступеню зв`язку між ознаками Варіація ознаки обумовлена різними факторами, деякі з цих факторів можна виділити, якщо статистичну сукупність розбити на групи по будь-якій ознаці. Тоді поряд з вивченням варіації ознаки і всієї сукупності в цілому стає можливим вивчити варіацію для кожної зі складових її групи, а також між цими групами. У найпростішому випадку, коли сукупність розчленована на групи по одному фактору, вивчення варіації досягається за допомогою обчислення й аналізу трьох видів дисперсії: загальної, міжгрупової, внутрішньогрупової. Загальна дисперсія вимірює варіацію ознаки по всій сукупності під впливом усіх факторів, що обумовлюють цю варіацію. Вона дорівнює середньому квадрату відхилень окремого значення ознаки від загальної середньої і може бути обчислена як проста і зважена дисперсія. Проста загальна дисперсія:
Зважена загальна дисперсія:
Міжгрупова дисперсія (d 2) характеризує систематичну варіацію результативної ознаки, обумовлену впливом ознаки фактора, покладеного в основу угруповання. Вона дорівнює середньому квадрату відхилень групових середніх від загальної середньої.
Внутрішньогрупова дисперсія відбиває випадкову варіацію, обумовлену впливом неврахованих факторів і незалежну від ознаки фактора, покладеного в основу угруповання. Вона дорівнює середньому квадрату відхилень окремих значень ознаки всередині групи від середньої арифметичної цієї групи і може бути обчислена як проста, чи як зважена дисперсія. Проста внутрішньогрупова дисперсія:
де j – кількість значень у групі.
Загальна середня з внутрішньогрупових дисперсій:
Відповідно до правила додавання дисперсій, загальна дисперсія дорівнює сумі середньої з внутрішньогрупових та міжгрупової дисперсії. Загальна дисперсія:
У статистичному аналізі широко використовується емпіричний коефіцієнт детермінації h2 - показник, що представляє собою частку міжгрупової дисперсії в загальній дисперсії результативної ознаки, та характеризуючий силу впливу групувальної ознаки на варіацію ознаки. Коефіцієнт детермінації:
Емпіричне кореляційне відношення -відображає тісноту зв'язку між групувальною та результативною ознакою. Приймає значення від 0 до 1 і дорівнює кореню квадратному з емпіричного коефіцієнту детермінації.
Якщо зв'язок є відсутнім, то кореляційне відношення дорівнює 0, а якщо зв'язок функціональний - 1. Чим значення кореляційного відношення ближче до 1, тим тісніше та ближче до функціональної залежності зв'язок між ознаками. Для якісної оцінки зв'язку на основі показника емпіричного кореляційного відношення можна скористатися кореляційними відносинами Чеддока:
сила слабкий помірний помітний тісний дуже зв'язку зв'язок зв'язок зв'язок зв'язок тісний зв'язок Приклад
1. Перетворимо наступні первинні дані грошового місячного доходу 25 домогосподарств (гр.од.) у ряд розподілу: Xi - 375;446;472;517;390;464;526;485;457;496;485;483; 412; 449;512;467;526;538;403;437; 504; 488; 454; 489; 472.
Першим кроком у побудові ряду розподілу є його ранжування, тобто розташування значень ознаки у зростаючому порядку: 375; 390; 403; 412; 437; 446; 449; 454; 457; 464; 467; 472; 472; 483; 485; 485; 488; 489; 496; 504; 512; 517; 526; 526; 538.
2. Ряд розподілу, побудований за кількісною ознакою, називається варіаційним. Побудуємо ряд розподілу, виражений у вигляді інтервалів. Такий ряд характеризує склад (структуру) досліджуваного явища, а також дозволяє судити про однорідність сукупності, закономірності розподілу і межах варіювання одиниць сукупності. Визначимо кількість груп, величину інтервалу, показники структури, кумулятивну чисельність, середину інтервалу. Кількість груп визначаємо за формулою Стерджеса: n = 1 + 3,322 lg N де N – число одиниць сукупності (=25). n = 1 + 3,322 lg25 = 5,6 або 5 (округлення відбувається до найближчого цілого). Результати розрахунку для деяких варіантів: N = 15 n = 4,9 приймаємо n = 5; N = 20 n = 5,3 приймаємо n = 5; N = 25 n = 5,6 приймаємо n = 6; N = 30 n = 5,9 приймаємо n = 6. Тоді розмір інтервалу можна визначити за формулою:
де n - кількість інтервалів; Х - значення варіюючої ознаки. Приймаємо розмір інтервалу 33. Округлення виконується до цілих, якщо у вихідних даних тільки цілі тризначні числа. В інших випадках округлення - до десятих (0,0). В результаті одержимо наступний інтервальний ряд розподілу грошового місячного доходу домогосподарств:
Як видно з даного ряду розподілу, більшість домогосподарств отримує місячний доход в межах 441 – 507 гр.од. Результати побудови ряду розподілу оформляються у вигляді таблиці. Таблиця 1.1.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.57 (0.006 с.) |

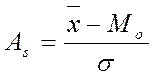 , або
, або  .
.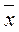 > Me>Mo (рис. 1), а лівосторонньої -
> Me>Mo (рис. 1), а лівосторонньої - 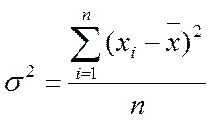
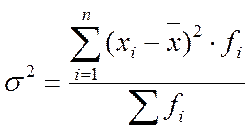

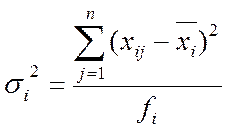


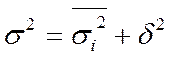
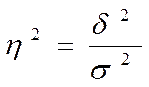
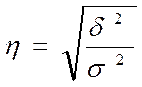
 0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99
0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99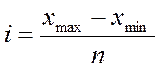 =
= 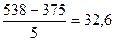 ,
,


