
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спостереження за двома зміннимиСодержание книги
Поиск на нашем сайте
Пробіт-графік.
Будується наступним чином.: Обчислимо емпіричну функцію розподілу Пробіт-графік – графік функції Використовується для: 1) Перевірки гіпотези
Пояснення: маємо:
2) Виявлення наявності аномальних спостережень у вибірці.
@Лекція 2 Імовірнісний графік
Ідея та ж сама. Зі спотвореною віссю у. Маємо множину Папір, де спотворюється масштаб називається імовірнісним папером. Якщо в якості розподілу взяти нормальний розподіл, то такий папір називається нормальним імовірнісним папером. Будуємо графік функції Висячі гістобари Використовується для перевірки нормальності вибірки. Нехай по вибірці Найбільш узгодженим нормальним розподілом для спостережень за
В центрах групування даних до графіка підвішуються прямокутні гістобари, довжина яких пропорційна відносній частоті потрапляння у відповідний інтервал групування. Якщо основа цих гістобар не суттєво відхиляється від осі Ох – гіпотеза про нормальність вибірки приймається.
Підвішена коренеграма
Спостереження за двома змінними Використовуються 1) Діаграма розсіювання. 2) Таблиця спряженості.
Діаграми розсіювання.
Таблиця спряженості Використовуються для представлення спостережень над номінальними, ординальними, кількісними дискретними (скінченими), кількісними неперервними (згрупованими змінними).
Де
Попередня обробка До попередньої обробки відносять: - розвідувальний аналіз; - обчислення основних характеристик спостережуваних величин; - видалення аномалій; - перевірка основних гіпотез; - перевірка на стохастичність вибірки.
Квантиль та процентні точки Квантилем рівня Квантилем рівня Вибіркові квантилі Q-процентною точкою
Квантиль та процентна точка пов’язані певним співвідношенням, а саме Введемо додаткові характеристики розподілу, похідні від перших двох. Приклади квантилей:
Класичний регресій ний аналіз Постановка: в якості апроксимації береться функція, лінійна по параметрах:
Тоді (2) можна переписати у вигляді:
Теорема Андерсона-Тейлора Вважаємо, що об’єм спостережень може зростати, тоді (3) можна переписати у вигляді
Доведемо деякі властивості оцінок
1 б) Потрібно визначити розмір компоненти Згідно а)
Лема1 Нехай
Застосуємо лему 1 до оцінки
3 а) б)
Довірчі області та інтервали для невідомих параметрів моделі. І. Довірча область для Згідно 4б) Лема2 Якщо, що (*) та (**) незалежні
ІІ Довірчий інтервал для Лема3
@Лекція 12 III. Інтервали Бонфероні Якщо для кожної компоненти побудувати довірчий інтервал з рівнями довіри
Треба знайти (Знак Звідси Пробіт-графік.
Будується наступним чином.: Обчислимо емпіричну функцію розподілу Пробіт-графік – графік функції Використовується для: 1) Перевірки гіпотези
Пояснення: маємо:
2) Виявлення наявності аномальних спостережень у вибірці.
@Лекція 2 Імовірнісний графік
Ідея та ж сама. Зі спотвореною віссю у. Маємо множину Папір, де спотворюється масштаб називається імовірнісним папером. Якщо в якості розподілу взяти нормальний розподіл, то такий папір називається нормальним імовірнісним папером. Будуємо графік функції Висячі гістобари Використовується для перевірки нормальності вибірки. Нехай по вибірці Найбільш узгодженим нормальним розподілом для спостережень за
В центрах групування даних до графіка підвішуються прямокутні гістобари, довжина яких пропорційна відносній частоті потрапляння у відповідний інтервал групування. Якщо основа цих гістобар не суттєво відхиляється від осі Ох – гіпотеза про нормальність вибірки приймається.
Підвішена коренеграма
Спостереження за двома змінними Використовуються 1) Діаграма розсіювання. 2) Таблиця спряженості.
Діаграми розсіювання.
Таблиця спряженості Використовуються для представлення спостережень над номінальними, ординальними, кількісними дискретними (скінченими), кількісними неперервними (згрупованими змінними).
Де
Попередня обробка До попередньої обробки відносять: - розвідувальний аналіз; - обчислення основних характеристик спостережуваних величин; - видалення аномалій; - перевірка основних гіпотез; - перевірка на стохастичність вибірки.
Квантиль та процентні точки Квантилем рівня Квантилем рівня Вибіркові квантилі Q-процентною точкою
Квантиль та процентна точка пов’язані певним співвідношенням, а саме Введемо додаткові характеристики розподілу, похідні від перших двох. Приклади квантилей:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.98.190 (0.011 с.) |


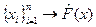 (Сімейство розподілів F з базовою функцією
(Сімейство розподілів F з базовою функцією  )
)

 У випадку, коли справедлива гіпотеза
У випадку, коли справедлива гіпотеза  пробіт-графік повинен уявляти собою майже пряму.
пробіт-графік повинен уявляти собою майже пряму.
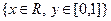 , яку розтягують за правилом
, яку розтягують за правилом  , де
, де 
 для спостереження величини
для спостереження величини 
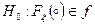 , то отримаємо майже пряму. Якщо маємо точки, що лежать осторонь, то перевіряємо їх на аномальність.
, то отримаємо майже пряму. Якщо маємо точки, що лежать осторонь, то перевіряємо їх на аномальність. підраховано мат. сподівання
підраховано мат. сподівання  та вибіркова дисперсія
та вибіркова дисперсія  .
. .
. Спочатку будуємо графік щільності з вибірки
Спочатку будуємо графік щільності з вибірки  Для кожного інтервалу групування даних визначають
Для кожного інтервалу групування даних визначають  - емпірична частота потрапляння в інтервал, а також теоретичне значення частоти
- емпірична частота потрапляння в інтервал, а також теоретичне значення частоти  згідно гіпотези про найбільш узгоджений нормальний розподіл. Потім на графіку відкладають такі різниці:
згідно гіпотези про найбільш узгоджений нормальний розподіл. Потім на графіку відкладають такі різниці:  . І якщо ці значення не значно відхиляються від нуля, то гіпотеза про нормальність вибірки приймається.
. І якщо ці значення не значно відхиляються від нуля, то гіпотеза про нормальність вибірки приймається. Маємо дві вибірки
Маємо дві вибірки  та
та  . Використовуються для з’ясування класу залежності між парою кількісних змінних, а також для з’ясування наявності аномальних спостережень у вибірці.
. Використовуються для з’ясування класу залежності між парою кількісних змінних, а також для з’ясування наявності аномальних спостережень у вибірці. яка має
яка має  - градацій, та змінна
- градацій, та змінна  яка має
яка має  - градацій.
- градацій.
 - кількість таких спостережень
- кількість таких спостережень 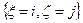 ., позначимо
., позначимо  та
та 
 для неперервної випадкової величини
для неперервної випадкової величини  називається значення
називається значення 
 , для границь якого виконується
, для границь якого виконується  та
та 
 визначаються як квантилі відповідних емпіричних розподілів.
визначаються як квантилі відповідних емпіричних розподілів. для неперервної випадкової величини.
для неперервної випадкової величини. 
 , для границь якого виконується
, для границь якого виконується  та
та 
 та
та 
 .
. ,
,  - верхній та нижній квартилі відповідно.
- верхній та нижній квартилі відповідно. називаються децилями.
називаються децилями. процентилі
процентилі називається величина
називається величина  .
.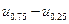 , тобто
, тобто  (Половина інтерквантильної широти
(Половина інтерквантильної широти 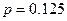 ,називається імовірнісним відхиленням.)
,називається імовірнісним відхиленням.) (1)
(1) .
.
 .
. – регресори. Деяка функція від векторів незалежних змінних
– регресори. Деяка функція від векторів незалежних змінних .
. (3)
(3) (8)
(8) 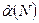 з об’ємом
з об’ємом  збігається до
збігається до  з ймовірністю 1
з ймовірністю 1 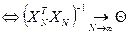 - (нульова матриця)
- (нульова матриця) 1 а)
1 а) (9)
(9)


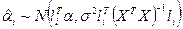 , де
, де  ,
, 
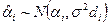
 ,
,  ,
,  , тоді виконується (*)
, тоді виконується (*) 



 співпадає з квадратичною формою (*)
співпадає з квадратичною формою (*) 


 ,
, 
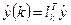 ,
, 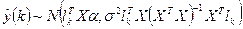 , де
, де 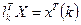 , а
, а 
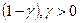

 (*)
(*) , де
, де  ,
,
 , де
, де 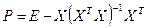 тому
тому  (10)
(10)  :
: 
 ,
, (11)
(11)  (**),
(**), 
 ,
,  ,
,  - матриці розмірності
- матриці розмірності  , тоді наступні квадратичні форми
, тоді наступні квадратичні форми  та
та  будуть незалежні тоді і тільки тоді, коли
будуть незалежні тоді і тільки тоді, коли 


 - довірча область (12)
- довірча область (12)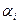
 (***)
(***) 
 - статистично незалежні.
- статистично незалежні. та
та  не обов’язково квадратна)
не обов’язково квадратна)
 (13)
(13)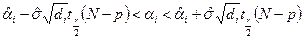
 ,
,  .
. - ймовірність того, що і-та компонента
- ймовірність того, що і-та компонента 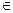 своєму довірчому інтервалу, який побудований за (13).
своєму довірчому інтервалу, який побудований за (13). - всі компоненти
- всі компоненти  .
. в ланцюжку з’являється внаслідок того, що
в ланцюжку з’являється внаслідок того, що  ).
).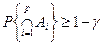 .
.


