
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Випадок скалярних спостереженьСодержание книги
Поиск на нашем сайте 1. Метод Грабса 2. Метод Томпсона Модифікація методу Грабса 3. Метод Тітьєна-Мура - Дозволяє з вибірки викидати декілька вимірів
4. Графічні методи: Розвідувальний аналіз.
II. Векторний випадок Нехай спостерігається 1. Критерій на базі F-статистики. 3.Підраховуються такі статистики: 2. Графічні методи: діаграма розсіювання
Кореляційний аналіз З’ясовує наявність статистичною зв’яжу між змінними, що досліджуються Схема по які досліджується наявність статистичного зв’язку.
I.Випадок кількісних змінних. Нехай є змінні (скалярні) Треба з’ясувати по спостереженнях за індексом кореляції для змінних
Властивості 1. 2. якщо 3. якщо Коефіцієнт детермінації @Лекція 5 Коефіцієнт кореляції. Характеристика парного статистичного зв’язку. Розглянемо нормальний випадок. Є дві величини Можна довести, що Властивості.
Якщо коефіцієнт кореляції прийняв проміжне значення, то перевіряємо гіпотезу Ця статистика має асимптотичний t-розподіл Стьюдента з степенями
Характеристика парного статистичного зв’язку в загальному випадку. Нехай спостерігаються - випадок групованих даних; - випадок не згрупованих даних. 1. Спостереження над залежною змінною 2. Функцію регресії Приклад:
Частинний коефіцієнт кореляції. Частинним коефіцієнтом кореляції для змінних Властивості частинного співпадають з властивостями звичайного коефіцієнта кореляції. Вибіркове значення коефіцієнта кореляції: При При Якщо коефіцієнт прийняв проміжне значення, то перевіряється гіпотеза Вона має Критична область – обасть великих і малих значень. Область прийняття має вигляд:
Множинний коефіцієнт кореляції. Розглянемо залежну змінну множинний коефіцієнт кореляції Множинний коефіцієнт детермінації: Властивості множинного коефіцієнта кореляції такі ж, як і звичайного коефіцієнта кореляції. Вибіркове значення. Функцію регресії По отриманим спостереженням методом найменших квадратів знаходимо оцінку
Методика використання.
Якщо Якщо Якщо Проаналізуємо наступну статистику: Вона має асимптотичний розподіл, який співпадає з F– розоділом з параметрами (p-1,n-p). Тоді область прийняття – це область невеликих значень:
Кореляційний аналіз порядкових змінних. Нехай Нехай відбуваються спостереження над
@Лекція 6
Якщо всі прояви об’єктів різні, то маємо При наявності по деякій зміні групи об’єктів з однаковим проявом досліджуваної властивості, цим об’єктам присвоюють ранг, який дорівнює середньому арифметичному номерів тих місць, які припали на цю групу об’єктів з нерозрізненими рангами. Такий ранг називається зв’язаний (об’єднаний). Будується таблиця рангів для доступу до об’єкта.
Характеристики парного статистичного зв’язку. Розглядаємо характеристики В якості характеристики парного зв’язку між змінними Властивості рангу коефіцієнта Спірмана: 1. 2. якщо 3. якщо якщо · Розглянемо випадок наявності Нерозрізнених рангів. В цьому випадку використовується модифікований коефіцієнт. Ранговий коефіцієнт Спірмана обчислюється за формулою: Коли коефіцієнт приймає проміжне значення, то перевіряємо гіпотезу Якщо об’єм вибірки невеликий, то перевіряємо по таблиці, при Область прийняття гіпотези: · Розглянемо іншу характеристику: коефіцієнт Кендала Ранговим коефіцієнтом Кендала для змінних
Властивості: 1. 2. якщо 3. якщо
Якщо є наявні нерозрізнені ранжировки, то використовують модифікований коефіцієнт Кендала: . Зауваження. При великих
Характеристика множинних рангових статистичних зв’язків. Нехай аналізується m змінних Коефіцієнтом конкордації для змінної
Властивості: 1. 2. якщо 3. якщо У випадку двох нерозрізнених рангів використовуємо модифікований коефіцієнт Якщо
Кореляційний аналіз номінальних змінних. Нехай Результат спостережень заноситься в таблицю спряженості. *(див. “Розвідувальний аналіз”), потім переходимо до характеристики парного статистичного зв’язку для номінальних змінних.
Вводимо статистику яка називається квадратичне спряження і позначається Коефіцієнти: 1. 2. 3. 4.
Властивості коефіцієнтів. 1. 2. @Лекція 7
Ентропією для змінної
Ймовірність, з якою приймається пара значень
Ентропією для пари
5. Інформаційна міра зв’язку
Властивості інформаційної міри зв’язку
Спробуємо визначити вибіркове значення. Спочатку визначимо вибіркове значення для ентропії При перевірці характеристики на значимість можливі два випадки:
Перший випадок якщо ми вибрали з 1 до 4, то перевірку на значимість роблять шляхом перевірки гіпотези з’ясувалося, що Тоді критична область, область великих значень та область прийняття гіпотези:
Другий випадок(з використанням інформаційної міри зв’язку) Виявилось, що така перетворена статистика: Оскільки ця статистика невід’ємна, то область прийняття гіпотези матиме такий вигляд (тобто,
Дисперсійний аналіз Нехай є деяка кількісна скалярна змінна
Дисперсійний аналіз займається побудовою математичної моделі зв’язку між цими змінними, а також їх аналізом.
Приклад З ’ясувати вплив сорту зернових на врожай. Залежна змінна – врожайність, якісна змінна – сорт зернових та тип міндобрив. Ця модель лінійна по всім параметрам, тому для її розв’язку напрошується метод найменших квадратів(МНК).
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.043 с.) |

 - найбільш підозрюваний на аномальний вимір є аномальним з рівнем значимості
- найбільш підозрюваний на аномальний вимір є аномальним з рівнем значимості 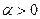 (1).
(1). (2)
(2) ,
, 
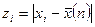 - абсолютне значення відхилень. По цій послідовності будується варіаційний ряд.:
- абсолютне значення відхилень. По цій послідовності будується варіаційний ряд.: - (3).Нехай є s-й член варіаційного ряду, то
- (3).Нехай є s-й член варіаційного ряду, то  . Перевіряємо на аномальність
. Перевіряємо на аномальність 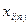 :
: , в якості
, в якості  (4), де
(4), де  це
це 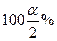 точка статистики
точка статистики  . Якщо (4) несправедливе, то
. Якщо (4) несправедливе, то  ця статистика має асимптотичний розподіл, t-розподіл Стьюдента з параметром
ця статистика має асимптотичний розподіл, t-розподіл Стьюдента з параметром 
 :
: 
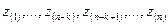 (5)
(5) (*)
(*) де
де  .
.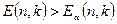 , де
, де  - квантиль рівня
- квантиль рівня  статистики
статистики  .
.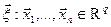
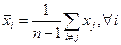 , далі підраховуємо значення коваріаційної матриці по всій вибірці, крім і-го виміру.
, далі підраховуємо значення коваріаційної матриці по всій вибірці, крім і-го виміру.
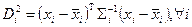 - відстань Махаланобіса.
- відстань Махаланобіса. зважена норма.
зважена норма.  - додатньовизначена матриця.
- додатньовизначена матриця.

 - індекс виміру для якого відстань Махаланобіса максимальна
- індекс виміру для якого відстань Махаланобіса максимальна  не є аномальним, тоді область прийняття гіпотези має вигляд:
не є аномальним, тоді область прийняття гіпотези має вигляд:  (*) де
(*) де  , це
, це  точка F розподілу з параметрами
точка F розподілу з параметрами  .
.  (
( 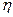 - залежна,
- залежна,  - незалежна).
- незалежна). ,
,  - умовна дисперсія.
- умовна дисперсія. 
 називається
називається 

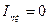 , то зв’язку між
, то зв’язку між  , то є функціональний зв’язок між ними
, то є функціональний зв’язок між ними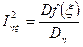 вказує яка частина варіації
вказує яка частина варіації 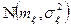 ,
, 
 ,
, 
 , вибіркове значення:
, вибіркове значення: 
 .
.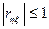
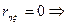 зв’язок між
зв’язок між  зв’язок між
зв’язок між  .
. . Якщо
. Якщо  , то і
, то і  .
. . При
. При  .
.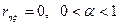 Для перевірки
Для перевірки  .
. свободи. Тоді логічно вважати, що
свободи. Тоді логічно вважати, що  область прийняття гіпотези
область прийняття гіпотези  - точки t-розподілу Стьюдента з
- точки t-розподілу Стьюдента з 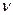 степенями свободи.
степенями свободи.
 спостережень.
спостережень.  спостережень по
спостережень по  ,
, 
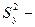 вибіркове значення дисперсії
вибіркове значення дисперсії 

 .Властивості такі ж, як і в індексу кореляції. З’ясувалося, що
.Властивості такі ж, як і в індексу кореляції. З’ясувалося, що  має асимптотичний розподіл, який тотожньо рівний
має асимптотичний розподіл, який тотожньо рівний  .
. . Припускаємо, що спостереження нормальні.
. Припускаємо, що спостереження нормальні. 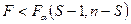 , де
, де  точка з параметрами
точка з параметрами  .
. апроксимують на деякому класі параметричних функцій з точністю до вектор – параметру
апроксимують на деякому класі параметричних функцій з точністю до вектор – параметру  .
.  .
.
 , далі отримуємо деяку апроксимацію функції регресії
, далі отримуємо деяку апроксимацію функції регресії  .
.

 будемо називати величину:
будемо називати величину:  , де
, де  - алгебраїчне доповнення для елемента
- алгебраїчне доповнення для елемента  у звичайній кореляційній матриці:
у звичайній кореляційній матриці: ,
,  - звичайний коефіцієнт кореляції.
- звичайний коефіцієнт кореляції. ,
,  .
. зв’язку не існує.
зв’язку не існує. зв’язок функціональний.
зв’язок функціональний. . Використовуємо статистику:
. Використовуємо статистику: , де
, де  кількість третіх змінних зафіксованих на певному рівні.
кількість третіх змінних зафіксованих на певному рівні.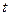 - розподіл Стьюдента з
- розподіл Стьюдента з 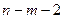 степенями свободи.
степенями свободи.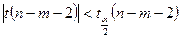 , де
, де  точка
точка  розподілу Стьюдента з
розподілу Стьюдента з 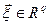 . Для з’ясування зв’язку використовується
. Для з’ясування зв’язку використовується , де
, де  ,
,  .
. .
. апроксимуємо на деякому класі параметричних функцій.
апроксимуємо на деякому класі параметричних функцій. ,
,  .
. .
. , то зв’язок неістотній.
, то зв’язок неістотній. , то зв’язок функціональний.
, то зв’язок функціональний. приймає проміжне значення, то перевіряється гіпотеза
приймає проміжне значення, то перевіряється гіпотеза 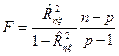

 залежна порядкова змінна і
залежна порядкова змінна і 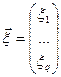 .
.
 .
.
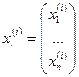 - ранжировка, де
- ранжировка, де  - ранг к-го об’єкту по і –й змінній, який вказує степінь прояву і –ї властивості для к-го об’єкту. Сама ранжировка – перестановка чисел від 1 до n.
- ранг к-го об’єкту по і –й змінній, який вказує степінь прояву і –ї властивості для к-го об’єкту. Сама ранжировка – перестановка чисел від 1 до n. - спостереження,
- спостереження,  - ранжировка.
- ранжировка. Змінні № об'єктів
Змінні № об'єктів











 ,
, 
 та
та  , де
, де 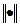 - норма Евкліда.
- норма Евкліда.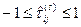 ;
; , тоді зв’язок відсутній;
, тоді зв’язок відсутній;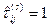 , то ранжировки по змінним співпадають,
, то ранжировки по змінним співпадають,  ;
; , тоді ранжировки протилежні, тобто
, тоді ранжировки протилежні, тобто  .
. , де
, де  - корегуючий коефіцієнт.
- корегуючий коефіцієнт.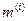 кількість груп об’єктів з нерозрізненними рангами по змінній
кількість груп об’єктів з нерозрізненними рангами по змінній  ,
, - кількість членів у
- кількість членів у 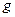 -й групі нерозрізнимих рангів по
-й групі нерозрізнимих рангів по  -й змінній.
-й змінній. .
.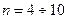 .
. , то розглядаємо статистику
, то розглядаємо статистику  , що має
, що має  - розподіл Стьюдента з
- розподіл Стьюдента з  степенями свободи.
степенями свободи. .
. , де
, де  - кількість перестановок сусідніх елементів у ранжировці
- кількість перестановок сусідніх елементів у ранжировці  , яка приводить її до ражировки
, яка приводить її до ражировки  .
. ;
; , тоді зв’язок відсутній;
, тоді зв’язок відсутній; , то ранжировки по змінним співпадають,
, то ранжировки по змінним співпадають,  ;
; , тоді ранжировки протилежні, тобто
, тоді ранжировки протилежні, тобто 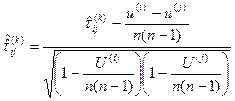 , де
, де 
 приймають протилежне значення, то перевіряємо його на значимість
приймають протилежне значення, то перевіряємо його на значимість . Якщо
. Якщо  .
. існує простий зв’язок:
існує простий зв’язок:  .
.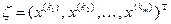 .
.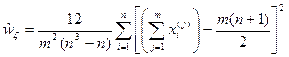 .
. ;
; , то ранжировки по змінним співпадають:
, то ранжировки по змінним співпадають:  ;
; , тоді відсутній зв’язок між ранжировками.
, тоді відсутній зв’язок між ранжировками. :
: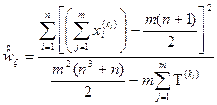 , де
, де  .
. . Коли
. Коли  , то за таблицею. Якщо
, то за таблицею. Якщо  , то розглядаємо статистику
, то розглядаємо статистику  , має
, має  - розподіл з
- розподіл з 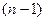 степенем свободи.
степенем свободи.

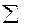





 - середнє значення квадратичної спряженості;
- середнє значення квадратичної спряженості; - коефіцієнт Пірсона;
- коефіцієнт Пірсона; - коефіцієнт Чупрова;
- коефіцієнт Чупрова; - коефіцієнт Крамера
- коефіцієнт Крамера , якщо коефіцієнт
, якщо коефіцієнт 
 , тоді зв’язок відсутній.
, тоді зв’язок відсутній. - якщо вони незалежні, то вони рівні, (або майже рівні).
- якщо вони незалежні, то вони рівні, (або майже рівні).
 дорівнює
дорівнює 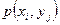 .
. називається величина
називається величина  .
.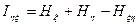 .
.

 зв’язок між
зв’язок між  ,
, ;
; 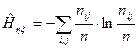

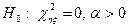 ,
, має хі-квадрат розподіл
має хі-квадрат розподіл 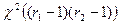 з
з  степенями свободи.
степенями свободи.
 ,де
,де  – кількість нульових елементів у таблиці спряженості.
– кількість нульових елементів у таблиці спряженості. .
.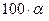 процентна точка хі-квадрат розподілу з
процентна точка хі-квадрат розподілу з  – сорт зернових,
– сорт зернових,  – всього сортів,
– всього сортів,  – тип міндобрив,
– тип міндобрив, 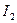 – всього міндобрив.
– всього міндобрив.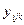 – спостерігаю і -й сорт зернових та j -й тип міндобрив на k -му полі.
– спостерігаю і -й сорт зернових та j -й тип міндобрив на k -му полі.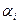 – вплив на залежну змінну,
– вплив на залежну змінну,  – вплив на якісну змінну.
– вплив на якісну змінну.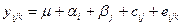 , де
, де  – невідомі параметри,
– невідомі параметри,  – помилка моделі,
– помилка моделі, – вплив взаємодії і -ї градації першої змінної та j -ї градації другої змінної на врожайність зернових.
– вплив взаємодії і -ї градації першої змінної та j -ї градації другої змінної на врожайність зернових.


