
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Довірчі інтервали та області для функції регресіїСодержание книги
Поиск на нашем сайте Нас цікавить довірчий інтервал і область для величин 1). Довірча область для вектора значень функції регресії Згідно (12) можна записати ліву частину у вигляді:
2). Довірча область для За властивістю 3) б):
Тоді наступна статистика: За властивістю 4) б):
Довірчий інтервал:
Перевірка на адекватність Перевірка на адекватність здійснюється шляхом перевірки спільномірності оцінки Випадки неадекватності: 1). або більше параметрів; 2). або менше параметрів. 1). Нехай модель істинна: Не всі регресори включені. Знаходимо оцінки Оцінка
2). Нехай в істинній моделі менше параметрів, ніж у вибраній, у якій є зайві. Тобто:
В цьому випадку:
Оцінка Ми втратили точності оцінки у вигляді:
@ Лекція 13 Ми розглядали випадок, коли модель містить більше або менше регресорів, ніж ідеальна. Коли регресорів менше – оцінка втрачає слушність. При наявності ж зайвих регресорів, хоча оцінка залишається слушною, її точність втрачається. Розглянемо методи перевірки адекватності моделі. В нашому розпорядженні є оцінка Припустимо, що крім цього нам надається можливість отримати додаткову вибірку спостережень Тоді оцінка по цій додатковій вибірці Один з методів перевірки адекватності полягає в перевірці такої гіпотези:
розглянемо статистики:
тоді Логічно вважати, що область прийняття буде При чому, як правило, намагаються вибирати об’єми вибірки таким, що Розглянемо тепер випадки, коли деякі з припущень моделі, яку ми розглядали не виконуються.
1. Випадок корельованих збурень Для нашої моделі Нехай тепер це не так, а Помножимо
Ввівши позначення отримаємо нову модель причому
Цю оцінку називають Марківською. На неї розповсюджуються всі раніше сформульовані властивості, все прекрасно, але радіти рано: треба знати матрицю Марківська оцінка (3) має наступні властивості:
Марківську оцінку можна розглядати також як розв’язок наступної оптимізаційної задачі:
Ця оцінка – це фактично один із прикладів, коли теорія – теорією, а практика – практикою.
2. Оцінки параметрів в умовах мультиколінеарності. Для Нехай Нехай В цьому випадку кажуть, що ми знаходимось в умовах строгої мультиколінеарності. Якщо ж умова (4) виконується тільки приблизно, то кажуть, що ми знаходимось в умовах мультиколінеарності. Проаналізуємо ці випадки:
Є різні підходи до розв’язання цієї проблеми. Викладемо такий:
Гребеневі оцінки (ridge-оцінки). Їх запропонував Херл в 1962р. Ідея проста: вводимо параметр
Введення цього зміщення відсуне і результат, але матриця
Теорема. Для гребеневої оцінки виконуються наступні властивості:
Зауваження 1. інколи на практиці використовують модифіковану оцінку
Зауваження 2. Графік
Бачимо, що існує
Для знаходження такого для кожної компоненти вектора Якщо ж стабілізації нема зовсім, то це означає, що ніякої мультиколінеарності взагалі немає, і можна використовувати класичну оцінку.
@Лекція 14 Нелінійний регресійний аналіз Моделі поділяються на два підкласи: 1) Внутрішньо лінійні 2) Внутрішньо нелінійні
Внутрішньо лінійні – це моделі які шляхом перетворень зводяться до розв’язання деякої лінійної задачі
Приклад1. Нехай модель має вигляд: Прологарифмуємо Введемо нові позначення: Отримаємо модель: Це можна використовувати лише у якості першого наближення. У випадку внутрішньо лінійних моделей як правило існують функції Оригінальна модель транспонується в наступну
З оцінки
Внутрішньо нелінійні – це моделі для яких не існує шляхів зведення до лінійної моделі Для (1) шукається Цей функціонал нелінійний по
Коваріаційний аналіз Треба побудувати модель залежності кількісної змінної від як від якісної так і від кількісної. Специфіка постановки задачі
На характеристику впливають як якісні так і кількісні змінні. Нехай Тоді модель класичного коваріаційного аналізу має вигляд:
Перепишемо модель матричному вигляді: Позначимо:
Тоді модель: Для знаходження оцінок параметрів моделі (4) використовується покроковий метод найменших квадратів.
Основні припущення для (4): 1) 2) стовпчики матриці 3) вважаємо, що лінійні обмеження враховані, тобто 4) Немає обмежень на 1), 2), 3), 4) (4)
Для розв’язку задачі кореляційного аналізу, враховуючи структуру моделі (4) використовують покроковий метод найменших квадратів:
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.008 с.) |

 та для всього
та для всього  .
. .
. ~
~  .
. ~
~ 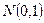 .
. ~
~ 
 ~
~ 

 .
. , отриманої на базі основної вибірки, з оцінкою
, отриманої на базі основної вибірки, з оцінкою  на базі спостережень з додаткової вибірки вимірів у фіксованій точці фазового простору.
на базі спостережень з додаткової вибірки вимірів у фіксованій точці фазового простору. , вибрана модель:
, вибрана модель:  .
. .
. :
:  .
. зміщена, тобто
зміщена, тобто  .
. .
. - вибрана.
- вибрана. ,
, 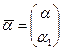 .
. незміщена, і
незміщена, і 
 - незміщена,
- незміщена,  .
. ,
,  Точність оцінки може збільшуватись.
Точність оцінки може збільшуватись.
 у фіксованій точці фазового простору.
у фіксованій точці фазового простору. , де
, де  .
. :
:  - незміщена
- незміщена 
 , – як відомо має
, – як відомо має  розподіл з
розподіл з 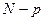 степенями свободи, аналогічно
степенями свободи, аналогічно

 .
. .
. (1) в класичному регресійному аналізі
(1) в класичному регресійному аналізі  .
. , де
, де  – кореляційна матриця. Спробуємо і для цього випадку отримати оцінку з тими ж хорошими властивостями, як і в класичному випадку.
– кореляційна матриця. Спробуємо і для цього випадку отримати оцінку з тими ж хорошими властивостями, як і в класичному випадку.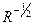 на (1):
на (1):  , тоді, згідно властивості лінійного перетворення нормально розподілених випадкових величин
, тоді, згідно властивості лінійного перетворення нормально розподілених випадкових величин  , тобто тут помилки уже будуть незалежними. Наступний вектор матиме розподіл
, тобто тут помилки уже будуть незалежними. Наступний вектор матиме розподіл
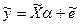 (2)
(2) і тоді будуємо оцінку класичним методом найменших квадратів:
і тоді будуємо оцінку класичним методом найменших квадратів: (3)
(3) , а на практиці вона зазвичай невідома. Часто можна знайти лише деяке наближення до неї, а тоді наближене значення
, а на практиці вона зазвичай невідома. Часто можна знайти лише деяке наближення до неї, а тоді наближене значення  може бути дуже далеко від реального значення, а потім ще й до
може бути дуже далеко від реального значення, а потім ще й до  треба шукати обернену... L
треба шукати обернену... L
 ефективна на класі всіх незміщених оцінок.
ефективна на класі всіх незміщених оцінок. є сильно слушною тоді і тільки тоді, коли
є сильно слушною тоді і тільки тоді, коли 

 , тобто повний по стовпчиках (
, тобто повний по стовпчиках ( – розмірність
– розмірність  ). Знімемо це припущення.
). Знімемо це припущення. ,
,  . Тоді, як результат, отримаємо, що класична оцінка просто не існує, оскільки матриця
. Тоді, як результат, отримаємо, що класична оцінка просто не існує, оскільки матриця  буде виродженою. Фактично це означає, що оцінка методом найменших квадратів буде не єдиною, і можна вибрати ту, яка найкраща для нас.
буде виродженою. Фактично це означає, що оцінка методом найменших квадратів буде не єдиною, і можна вибрати ту, яка найкраща для нас. :
:  (4)
(4)
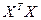 виходить погано обумовленою (існують власні числа близькі нуля)
виходить погано обумовленою (існують власні числа близькі нуля) може бути дуже великою).
може бути дуже великою). і збурюємо
і збурюємо  , де
, де  , але досить мале. (5)
, але досить мале. (5)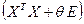 вже не буде погано обумовленою. Виявилось також, що при деякому
вже не буде погано обумовленою. Виявилось також, що при деякому  , де
, де  .
. .
.  , де зміщення
, де зміщення  , а
, а  .
. (перша рівність – просто позначення).
(перша рівність – просто позначення).





 , тобто оцінка зміщена.
, тобто оцінка зміщена. 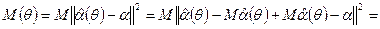


 , де
, де  – діагональна матриця,
– діагональна матриця,  ; тоді
; тоді , ну а далі все прозоро:
, ну а далі все прозоро: для моделі
для моделі 
 потім знаходимо
потім знаходимо 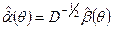
 :
: таке, що ridge- оцінка буде мати середньоквадратичну похибку меншу ніж класична оцінка.
таке, що ridge- оцінка буде мати середньоквадратичну похибку меншу ніж класична оцінка. Зауваження 3.
Зауваження 3. і за
і за  ,
,  (1), де
(1), де  - помилка моделі,
- помилка моделі, , де
, де  - скаляр
- скаляр
 ,
,  ,
,  ,
, 
 - лінійна відносно параметрів.
- лінійна відносно параметрів.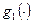 ,
,  ,
,  (1)
(1) ,де
,де  ,
, 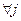 (2)
(2) можемо за допомогою системи однозначно визначити оцінку
можемо за допомогою системи однозначно визначити оцінку 
 - вектор незалежних якісних змінних,
- вектор незалежних якісних змінних,  - вектор кількісних змінних,
- вектор кількісних змінних, 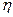 - залежна скалярна кількісна змінна.
- залежна скалярна кількісна змінна. - спостереження над
- спостереження над  ,
,  та
та  ,
,  ,
,  ,
,  ,
,  ,
, 
 (4)
(4) не залежать від умов експерименту.
не залежать від умов експерименту. ,
,  (4’)
(4’)


