
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади розв’язування навчальних завданьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приклад 5.1. Компанія контролює три фабрики А 1, А 2, А 3, здатні виготовляти 150, 60 та 80 тис. од. продукції щотижня. Компанія уклала договір із чотирма замовниками В 1, В 2, В 3, В 4, яким потрібно щотижня відповідно 110, 40, 60 та 80 тис. од. продукції. Вартість виробництва та транспортування 1000 од. продукції замовникам з кожної фабрики наведено в таблиці.
Визначити для кожної фабрики оптимальний план перевезення продукції до замовників, що мінімізує загальну вартість виробництва і транспортних послуг. Побудова математичної моделі. Нехай xij — кількість продукції, що перевозиться з і -ї фабрики до j -го замовника
Економічний зміст записаних обмежень полягає ось у чому: уся вироблена на фабриках продукція має вивозитися до замовників повністю. Аналогічні обмеження можна записати відносно замовників: продукція, що надходить до споживача, має повністю задовольняти його попит. Математично це записується так:
Загальні витрати, пов’язані з виробництвом і транспортуванням продукції, складаються як добуток обсягу перевезеної продукції та питомої вартості перевезень за відповідним маршрутом і за умовою задачі мають бути мінімальними. Тому Z = 4 × x 11 + 4 × x 12 + 2 × x 13 + 5 × x 14 + 5 × x 21 + 3 × x 22 + x 23 + У цілому математичну модель поставленої задачі можна записати так: Z = 4 x 11 + 4 x 12 + 2 x 13 + 5 x 14 + 5 x 21 + 3 x 22 + x 23 + 2 x 24 +
Розв’язування. Розв’язування задачі подамо в таблицях, які назвемо транспортними. Перший опорний план задачі побудуємо методом мінімальної вартості.
Тому Z = 4 × 110 + 5 × 40 + 1 × 60 + 1 × 40 + 2 × 40 = 820 ум. од. Перший опорний план транспортної задачі вироджений, оскільки кількість заповнених клітинок у таблиці дорівнює п’яти, а (m + n – 1) = 3 + 4 – 1 = 6. Для подальшого розв’язування задачі необхідно в одну з порожніх клітинок записати «нульове перевезення» так, щоб не порушити опорності плану, тобто можна зайняти будь-яку вільну клітинку, яка не утворює замкненого циклу. Наприклад, заповнимо клітинку А 2 В 4. Тепер перший план транспортної задачі є невиродженим, і його можна перевірити на оптимальність за допомогою методу потенціалів. На основі першої умови оптимальності ui + vj = cij складемо систему рівнянь для визначення потенціалів плану:
Записана система рівнянь є невизначеною, і один з її розв’язків дістанемо, якщо, наприклад, v 4 = 0. Тоді всі інші потенціали однозначно визначаються: u 1 = 5, u 2 = 2, u 3 = 2, v 1 = –1, Далі згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності ui + vj ≤ cij (для порожніх клітинок таблиці): А 1 B 2: u 1 + v 2 = 5 + (–1) = 4 = 4; А 1 B 3: u 1 + v 3 = 5 + (–1) = 4 > 2; А 2 B 1: u 2 + v 1 = 2 + (–1) = 1 < 5; А 2 B 2: u 2 + v 2 = 2 + (–1) = 1 < 3; А 3 B 1: u 3 + v 1 = 2 + (–1) = 1 < 2; А 3 B 3: u 3 + v 3 = 2 + (–1) = 1 < 4. Умова оптимальності не виконується для клітинки А 1 B 3. Порушення D13 = (u 1 + v 3) – c 13 = 4 – 2 = 2 записуємо в лівому нижньому кутку відповідної клітинки. Перший опорний план транспортної задачі є неоптимальним. Тому від нього необхідно перейти до другого плану, змінивши співвідношення заповнених і порожніх клітинок таблиці. Потрібно заповнити клітинку А 1 B 3, в якій є єдине порушення умови оптимальності. Ставимо в ній знак «+». Для визначення клітинки, що звільняється, будуємо цикл, починаючи з клітинки А 1 B 3, та позначаємо вершини циклу почергово знаками «–» і «+». Тепер необхідно перемістити продукцію в межах побудованого циклу. Для цього у вільну клітинку А 1 B 3 переносимо менше з чисел хij, які розміщуються в клітинках зі знаком «–». Одночасно це саме число хij додаємо до відповідних чисел, що розміщуються в клітинках зі знаком «+», та віднімаємо від чисел, що розміщуються в клітинках, позначених знаком «–». У даному випадку Отже, другий опорний план транспортної задачі матиме такий вигляд:
Тому Z 2 = 4 × 110 + 2 × 40 + 1 × 20 + 2 × 40 + 1 × 40 + 2 × 40 =740 ум. од. Новий план знову перевіряємо на оптимальність, тобто повторюємо описані раніше дії. Другий план транспортної задачі також неоптимальний (порушення для клітинки А 3 B 1). За допомогою побудованого циклу виконаємо перехід до третього опорного плану транспортної задачі і дістанемо таку таблицю:
Тому Z 3 = 4 × 90 + 2 × 60 + 2 × 60 + 2 × 20 + 1 × 40 + 2 × 20 = 720 ум. од. Перевірка останнього плану на оптимальність за допомогою методу потенціалів показує, що він оптимальний. Тому
За оптимальним планом перевезень перший замовник отримує 90 тис. од. продукції з першої фабрики та 20 тис. од. — з третьої. Другий споживач задовольняє свій попит за рахунок виробництва та перевезення 40 тис. од. продукції з третьої фабрики і т. д. При цьому загальна вартість виробництва та перевезення всієї продукції є найменшою і становить 720 ум. од. Приклад 5.2. Районне агропромислове об’єднання складається з трьох господарств А 1, А 2, А 3, що спеціалізуються на вирощуванні ранніх овочів. Кожне господарство щотижня збирає відповідно 50, 30 та 20 т овочів, які необхідно відправляти в чотири магазини B 1, B 2, B 3, B 4. Магазини бажають отримувати ранні овочі в кількості відповідно 30, 30, 10 та 20 т. Вартість перевезення 1 т овочів від господарства до магазинів наведено в таблиці.
Визначити такий план перевезення овочів до магазинів, за якого загальні витрати агропромислового об’єднання будуть найменшими. Побудова математичної моделі. Нехай хij — кількість тон овочів, які перевозять з і -го господарства j -го магазину ( Z = 2 x 11 + 3 x 12 + 4 x 13 + 2 x 14 + 5 x 21 + 7 x 22 + x 23 + за обмежень
Знак «≤» у перших трьох обмеженнях задачі пояснюється тим, що за умовою транспортна задача є відкритою:
У такій ситуації, коли попит менший за пропозицію, частина овочів залишиться в господарствах і фактично буде вивезено менше, ніж зібрано. Розв’язування. Щоб визначити оптимальний план поставленої задачі, її необхідно збалансувати, тобто звести до закритого типу. Це виконується шляхом уведення додаткового, умовного споживача B 5 із попитом B 5 = 100 – 90 = 10 т. Вартість перевезення одиниці продукції до умовного споживача дорівнює нулю. Перший опорний план транспортної задачі побудуємо методом подвійної переваги.
Перший опорний план є виродженим, і тому в клітинку, наприклад A 2 B 4, поставимо нуль і вважатимемо її заповненою. Перевірка плану за допомогою потенціалів показує, що він є неоптимальним. Перехід до другого опорного плану виконується шляхом заповнення клітинки A 3 B 2 згідно із побудованим циклом. Зазначену клітинку включено до циклу тому, що в разі кількох однакових найбільших порушень (D21 = D32 = 1) заповнюють таку клітинку таблиці, яка має меншу вартість перевезення одиниці продукції (с 32 < c 21). Другий план транспортної задачі наведемо у вигляді таблиці:
Умова оптимальності для цього опорного плану виконується, і тому можна записати:
Z min = 2 × 30 + 3 × 20 + 1 × 10 + 4 × 10 + 4 × 10 + 2 × 10 = 320 ум. од. Згідно з оптимальним планом потреба магазинів у ранніх овочах задовольняється завдяки повному вивезенню продукції з першого та третього господарств і лише частково — з другого (залишок дорівнює 10 т). У цьому разі загальна вартість усіх перевезень буде найменшою і становитиме 230 ум. од. Але виявляється, що розглянута транспортна задача має ще один альтернативний оптимальний план. Ознакою цього є виконання умови оптимальності для порожньої клітинки: ui + vj = cij. В останній таблиці це справджується для порожньої клітинки A 2 B 1: u 1 + v 1 = 0 + 5 = с 21 = 5. Щоб отримати альтернативний оптимальний план, достатньо заповнити зазначену клітинку таблиці, виконавши перерозподіл продукції за таким циклом:
Наведемо транспортну таблицю, що відповідає другому оптимальному плану задачі.
Тому
Z min = 2 × 20 + 3 × 30 + 5 × 10 + 1 × 10 + 2 × 20 = 230 ум. од. Другий оптимальний план задачі формулюється так. Перевезти з першого господарства 20 т овочів до першого магазину та 30 т — до другого; з другого господарства — 10 т до першого магазину та 10 т овочів до третього, залишаючи невивезеними 10 т, а також з третього господарства до четвертого магазину — 20 т овочів. У цьому разі загальні транспортні витрати становитимуть 230 ум. од. і також будуть найменшими.
Приклад 5.3. Три нафтопереробних заводи А 1, А 2, А 3, із максимальною щоденною продуктивністю відповідно 30, 20, 15 тис. т бензину забезпечують чотири бензосховища B 1, B 2, B 3, B 4, потреба яких становить відповідно 10, 20, 25 та 20 тис. т. бензину. Бензин транспортується до бензосховищ за допомогою трубопроводів. Вартість перекачування 1000 т бензину від заводів до сховищ (в умовних одиницях) наведено в таблиці.
Cформулювати та розв’язати відповідну транспорту задачу з неодмінним виконанням таких умов: 1) повністю задовольнити попит бензосховища B 4; 2) недопостачання бензину до сховища B 2 штрафується 5 ум. од. вартості за кожні 1000 т бензину; 3) у зв’язку з виконанням ремонтних робіт на трубопроводі постачання бензину із заводу А 1 до сховища B 1 тимчасово неможливе. Розв’язування. Визначимо, до якого типу належить транспортна задача:
За умовою транспортна задача є відкритою, незбалансованою. Зведення її до закритого типу потребує введення додаткового фіктивного постачальника А 4 з продуктивністю а 4 = 75 – 65 = 10 (тисяч тон). Кількість бензину, що «відправляється» фіктивним заводом до бензосховищ, в оптимальному плані означатиме обсяг незадоволеного попиту в цьому пункті призначення. Тому для виконання першої додаткової вимоги задачі необхідно блокувати клітинку фіктивного постачальника А 4 та споживача B 4, записавши в ній досить високу вартість М. Тоді в оптимальному плані транспортної задачі ця клітинка обов’язково буде незаповненою. Виконання другої умови задачі забезпечується тим, що в рядку фіктивного постачальника у стовпчику B 2 вартість транспортування 1000 т бензину дорівнюватиме 5 ум. од. замість нуля. Оскільки неможливо транспортувати бензин від заводу А 1 до сховища B 1, необхідно також блокувати маршрут А 1 B 1. Для цього в зазначеній клітинці замість с 11 = 4 записуємо величину М. З огляду на викладене таблиця для першого плану транспортної задачі має такий вигляд (початковий опорний план побудовано методом апроксимації Фогеля).
Отже, перший опорний план задачі неоптимальний. Найбільше порушення умови оптимальності відповідає порожнім клітинкам А 4 B 1 та А 3 B 3 таблиці. Оскільки обидві вони мають однаковий коефіцієнт с 41 = с 43 = 0, то для заповнення можна вибрати будь-яку з них, наприклад А 4 B 1. Перехід до другого плану виконується за таким циклом:
При цьому заблокована клітинка А 4 B 4 звільняється. Подальше розв’язування задачі подано у вигляді таблиць.
В останній таблиці маємо оптимальний план транспортної задачі. Тому
Z min = 5 × 5 + 5 × 25 + 5 × 20 + 3 × 15 = 245 ум. од.
Через незбалансованість поставленої транспортної задачі спостерігатиметься недопостачання бензину до першого бензосховища в кількості 10000 т. Загальні витрати на транспортування в цьому разі будуть найменшими і становитимуть 245 ум. од. Альтернативний оптимальний план дістанемо, заповнивши клітинку А 4 В 3 (для неї u 4 + v 3 = c 43) згідно з таким циклом:
Тоді можна записати:
Z min = 5 × 15 + 3 × 15 + 5 × 20 + 1 × 10 + 3 × 15 = 245 ум. од. Мінімальні загальні витрати на транспортування в розмірі 245 ум. од. відповідають також ще одному оптимальному плану задачі, згідно з яким третє бензосховище отримає на 10000 т бензину менше, ніж потребує. Існування двох альтернативних оптимальних планів розглянутої транспортної задачі розширює можливості стосовно остаточного прийняття рішення.
Зі схеми бачимо, що на перший склад надходить лише 300 + 300 + 700 = 1300 од. продукції, тобто його місткість використовується не повністю (D 1 D 1 = 1200 од.). Це виникає внаслідок прямих поставок продукції за маршрутом А 1 В 2 у кількості 700 од. і А 3 В 4 — у кількості 500 од. Розглянута транспортна задача має ще один альтернативний оптимальний план, який відрізняється від першого лише в частині, що стосується перевезення продукції зі складів до третього та п’ятого споживачів. Поряд із розглянутою у транспортних задачах із проміжними пунктами можуть зустрічатися також такі ситуації: 1. Незбалансованість транспортної задачі ( 2. Місткість проміжних пунктів не відповідає загальному обсягу продукції постачальників: а) коли 3. Місткість проміжних пунктів не відповідає загальній потребі споживачів: а)
5.2. Приклади та завдання для самостійної роботи Розв’язати наведені далі транспортні задачі
5.12 Передбачено штрафи за недопостачання одиниці продукції до споживачів В 1, В 2, В 3 у розмірі відповідно 5, 3 та 2 ум. од. Визначити оптимальний план такої транспортної задачі:
5.13 Розв’язати транспортну задачу:
якщо вартість зберігання одиниці невивезеної продукції у постачальників А 1, А 2, А 3, А 4 дорівнює відповідно 5, 4, 2 та 3 ум. од.
5.14 Розв’язати транспортну задачу:
якщо штрафи за недопостачання продукції споживачам В 1, В 2, В 3 становлять відповідно 6, 4 та 8 ум. од.
5.15 Розв’язати транспортну задачу за умови, що вартість зберігання невивезеної продукції в постачальників А 1, А 2, А 3 дорівнює відповідно 8, 7 та 5 ум. од. за одиницю продукції:
5.16 У транспортній задачі загальний обсяг виробництва продукції перевищує загальний попит. Припустимо, що вартість зберігання одиниці продукції, яка не вивозиться від постачальників А 1, А 2, А 3, А 4, дорівнює відповідно 7, 3, 4 та 8 ум. од. Визначити оптимальний план задачі:
5.17 У незбалансованій транспортній задачі загальний попит перевищує загальний обсяг виробництва на 10 ум. од. продукції. За недопостачання продукції споживачам умовою задачі передбачаються штрафи в розмірі 6 та 4 ум. од. за кожну одиницю продукції відповідно для першого та другого постачальників. Визначити оптимальний план такої транспортної задачі:
5.18 У незбалансованій транспортній задачі призначено плату за зберігання кожної одиниці невивезеної продукції від постачальників у розмірі відповідно 5, 4 та 3 ум. од.. Визначити оптимальний план задачі, якщо висунуто таку додаткову умову: уся продукція від другого постачальника має бути вивезена повністю для того, щоб звільнилося місце для нової продукції.
5.19 Розв’язати транспортну задачу:
Додаткова умова: попит третього споживача задовольнити повністю. 5.20 Розв’язати транспортну задачу:
Додаткова умова: ресурси четвертого постачальника використати повністю. 5.21 Розв’язати транспортну задачу:
Додаткова умова: попит першого та четвертого споживачів задовольнити повністю.
5.22 Розв’язати транспортну задачу:
Додаткова умова: ресурси першого та третього постачальників використати повністю. 5.23 У транспортній задачі визначити оптимальний план за умови повного задоволення потреб першого та другого споживачів:
5.24 Розв’язати транспортну задачу:
5.25 Додаткова умова: ресурси першого та другого постачальників в оптимальному плані використати повністю. 5.26 Визначити оптимальний план транспортної задачі:
в якій потрібно повністю задовольнити попит третього споживача та неможливо виконувати перевезення за маршрутами А 1 В 2 та А 3 В 1.
5.27 Знайти оптимальний план транспортної задачі:
Додаткові умови: повністю використати ресурси четвертого постачальника та не виконувати перевезення за маршрутами А 2 В 3 та А 3 В 4.
5.28 Розв’язати транспортну задачу:
Додаткова умова: попит другого споживача задовольнити повністю та за маршрутом А 2 В 3 перевезти рівно 10 од. продукції.
5.29 Визначити оптимальний план транспортної задачі:
якщо ресурси четвертого постачальника потрібно використати повністю і за маршрутом А 4 В 3 перевезти 20 од. продукції. 5.30 Розглянути транспортну задачу, в якій необхідно перевезти деяку продукцію від постачальників А 1, А 2, А 3 до споживачів В 1, В 2, В 3, В 4 через проміжні пункти D 1, D 2, D 3. Запаси продукції у постачальників, попит споживачів та місткість складів відповідно ai = (200; 220; 380), bj = (150; 50; 350; 250), di (j)= (350; 200; 400). Вартість перевезення одиниці продукції від постачальників на склади та зі складів до споживачів наведено в таблицях.
Перевезення продукції зі складу на склад неприпустиме. Визначити оптимальний план поставленої транспортної задачі, який забезпечує найменші загальні витрати на перевезення необхідної продукції від постачальників до споживачів.
5.31 Розв’язати двохетапну транспортну задачу ai = (400; 200; 300), bj = (300; 200; 350; 50), di (j)= (250; 250; 500).
Неприпустиме перевезення продукції зі складу на склад. 5.32 Розглянути транспортну задачу з проміжними пунктами, в якій кількість складів менша за ресурси постачальників. У такій ситуації дозволене транзитне перевезення продукції безпосередньо від постачальників А 1 та А 2 до першого споживача. Вартість перевезення одиниці продукції за транзитними маршрутами А 1 В 1 та А 2 В 1 становить відповідно 6 та 5 ум. од.; ai = (200; 300), bj = (250; 100; 150), di (j)= (100; 150; 150).
Визначити оптимальний план поставленої задачі.
5.33 Розглянути двохетапну транспортну задачу, в якій дозволене пряме перевезення продукції від першого постачальника до споживачів В 1, В 2, В 3, В 4. Вартість перевезення одиниці продукції за транзитними маршрутами дорівнює відповідно 3, 4, 5, 3 ум. од.; ai = (300; 200; 100), bj = (150; 50; 200; 200), di (j)= (250; 250).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 744; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.72 (0.01 с.) |

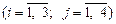 . Оскільки транспортна задача за умовою є збалансованою, закритою
. Оскільки транспортна задача за умовою є збалансованою, закритою 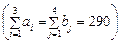 , то математична модель задачі матиме вигляд
, то математична модель задачі матиме вигляд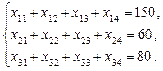
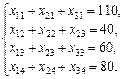
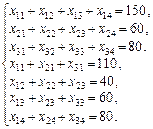
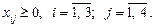



 A 1= 150
A 1= 150
 A 2= 60
A 2= 60
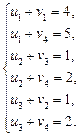
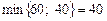 , тобто
, тобто 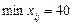 . Виконавши перерозподіл продукції згідно із записаними правилами, дістанемо такі нові значення: клітинка А 1 B 3 — 40 од. продукції, А 2 B 3 – (60 – 40) = 20 од., А 2 B 4 – (0 + 40) = 40 од. Клітинка А 1 B 4, звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписують у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості, тобто дорівнювати (n + m – 1).
. Виконавши перерозподіл продукції згідно із записаними правилами, дістанемо такі нові значення: клітинка А 1 B 3 — 40 од. продукції, А 2 B 3 – (60 – 40) = 20 од., А 2 B 4 – (0 + 40) = 40 од. Клітинка А 1 B 4, звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписують у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості, тобто дорівнювати (n + m – 1). A 1= 150
A 1= 150
 ;
;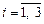 ;
; 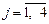 ). Тоді економіко-математична модель поставленої задачі має такий вигляд:
). Тоді економіко-математична модель поставленої задачі має такий вигляд: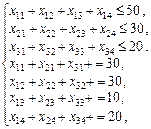
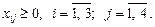
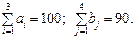
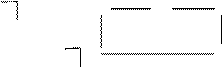 A 2= 30
A 2= 30
 ;
;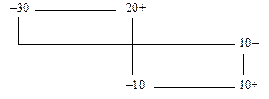
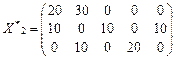 ;
;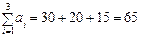 ,
, 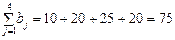 .
. A 1= 30
A 1= 30
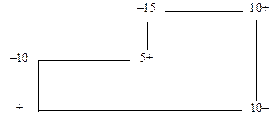


 A 1= 30
A 1= 30

 A 2= 20
A 2= 20
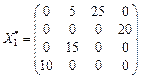 ,
,
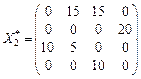 ,
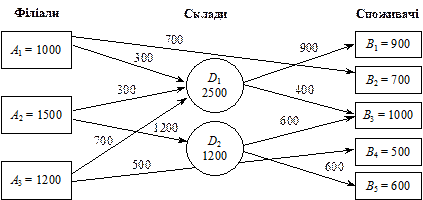
,
 ). У цьому разі необхідно ввести або фіктивного постачальника, або фіктивного споживача, звівши задачу до закритого типу.
). У цьому разі необхідно ввести або фіктивного постачальника, або фіктивного споживача, звівши задачу до закритого типу. (у цьому разі потрібно або ввести фіктивний проміжний пункт, і кількість продукції, що «перевозитиметься» до нього, має означати невивезену частину продукції відповідного постачальника, або дозволити транзитні перевозки за обсягом не менш як
(у цьому разі потрібно або ввести фіктивний проміжний пункт, і кількість продукції, що «перевозитиметься» до нього, має означати невивезену частину продукції відповідного постачальника, або дозволити транзитні перевозки за обсягом не менш як 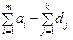 (од.)); б) коли
(од.)); б) коли 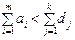 (у цьому разі немає потреби вводити фіктивного постачальника і заздалегідь зрозуміло, що місткість проміжних пунктів повністю не використовуватиметься).
(у цьому разі немає потреби вводити фіктивного постачальника і заздалегідь зрозуміло, що місткість проміжних пунктів повністю не використовуватиметься).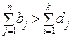 (у цьому разі потрібно або ввести фіктивний проміжний пункт, і кількість продукції, що «перевозитиметься» від нього до споживача В, має означати незадоволений попит відповідного споживача, або дозволити пряме перевезення продукції від постачальників до споживачів за обсягом не менш як
(у цьому разі потрібно або ввести фіктивний проміжний пункт, і кількість продукції, що «перевозитиметься» від нього до споживача В, має означати незадоволений попит відповідного споживача, або дозволити пряме перевезення продукції від постачальників до споживачів за обсягом не менш як 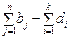 (од.)); б)
(од.)); б)  (аналогічно п. 2б).
(аналогічно п. 2б).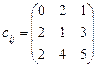 .
.
 .
.
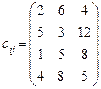 .
.
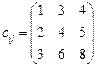 .
.
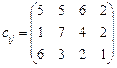 .
.
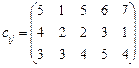 .
.
 .
.
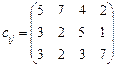 .
.
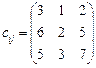 .
.
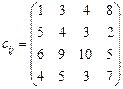 .
.
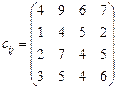 .
.
 .
.
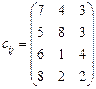 ,
,
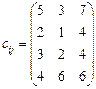 ,
,
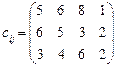 .
.
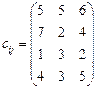 .
.
 .
.
 .
.
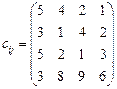 .
.
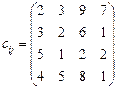 .
.
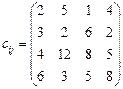 .
.
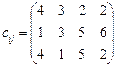 .
.
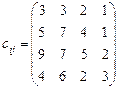 .
.
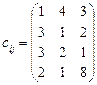 .
.
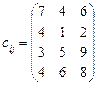 ,
,
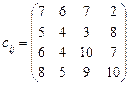 .
.
 .
.
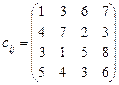 ,
,



