
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади розв’язання типових задач. ⇐ ПредыдущаяСтр 2 из 2
Приклад 1. Знайти добуток матриць.
Розв’язування. Спочатку впевнимось, що матриця А має обернену А-1.
Отже, матриця А має обернену А-1, яку знайдемо за формою Алгебраїчними доповненнями до елементів матриці А будуть:
Таким чином, одержали
Приклад 4. Розв’язати за правилами систему рівнянь
Розв’язування. Задача неоднорідна система 3 лінійних алгебраїчних рівнянь з трьома невідомими. Основний визначник цієї системи.
Тому, згідно з правилом Крамера, задана система має єдиний розв’язок, який знайдено за формулами
∆к
xк = ∆(А), k = 1,2,…. -, n
Тепер за формулами знаходимо ∆1 -93
х1 = = = -3 ∆(А) 31
∆2 62
х2 = = = 2 ∆(А) 31
∆3 31
х3 = = = 1 ∆(А) 31 Розв’язком цієї системи буде (-3; 2; 1)
Приклад 5. Розв’язати систему рівнянь Розв’язування. Задана система 3 рівняння з 4 невідомими. Виконаємо елементарні перетворення з розширеною матрицею.
r (А) = r (А) = 2. Знайдемо мінор другого порядку, який не дорівнює нулю.
Мінор, який не дорівнює нулю, має порядок, рівний рангу r = r (А) = r (А), називають базисним мінором, тому обраний нами мінор = базисний. Невідомі х1 та х2, для яких елементи базисного мінору є коефіцієнтами називають базисними невідомими. Інші невідомі системи х3 та х4 – вільні. Останній вигляд розширеної матриці відповідає такій системі:
Вільні невідомі перенесли у праву частину системи. Ми одержали базисні змінні х1 та х2 як функції х3 та х4 Вільними невідомими х3 та х4 можна давати будь – які значення: х3 = С1, х4 = С2, де С1 та С2 – довільні стали. Отже, одержуємо нескінченну кількість розв’язків системи випадку:
Розділ 4: Елементи теорії ймовірності.
Література:
Методичні рекомендації. Теорія ймовірностей вивчає закономірності у випадкових подіях. Основними поняттями теорії ймовірності є випробування і події. Під випробуванням (дослідом) розуміють реалізацію комплексу умов, внаслідок якого неодмінно відбудеться яка-небудь подія. Наприклад: кидання монети – випробування; поява герба чи цифри – події. Випадковою подією називають подію, пов’язану з даним випробуванням, яка при здійсненні випробування може відбутися, а може й не відбутися. Слово “випадкова” для стислості часто опускають і говорять просто подія. Наприклад, постріл по цілі – це дослід, випадкові події у цьому досліді – попадання в ціль або промах. Подія називається вірогідною, якщо в результаті досліду вона обов’язково відбудеться і неможливою, якщо вона не може відбутися. Наприклад: випадання не більше шести очків при киданні однієї гральної кості – вірогідна подія; випадання десяти очок при киданні однієї гральної кості – неможлива подія. Події називаються несумісними, якщо ніякі дві з них не можуть відбутись одночасно. Наприклад: попадання і промах при одному пострілі – це несумісні події. Говорять, що декілька подій у даному досліді утворюють повну систему подій, якщо в результаті досліду неодмінно повинно відбутися хоча б одна з них. Наприклад: при киданні гральної кості події, які полягають у випаданні одного, двох, трьох, чотирьох, п’яти і шести очок, утворюють повну систему подій. Події називають рівноможливими, якщо ні одна з них не є об’єктивно більш можлива, ніж інша. Наприклад при киданні монети випадання герба чи числа – події рівно можливі. Кожна подія має якусь степінь можливості. Числова міра степеня об’єктивної можливості події – це ймовірність події. Ймовірність події А позначається Р(А). Нехай з системи n- несумісних рівно можливих наслідків випробувань m- наслідків сприяють події А. Тоді ймовірність події А обчислюється по формулі:
Р(А) =
Ця формула носить назву класичного означення ймовірності. Якщо В – вірогідна подія, то m = n, отже Р(В) = 1; Якщо С – неможлива подія, то m = 0, отже Р(С) = 0; Якщо А – вірогідна подія, то m ≤ n, отже Р(А) ≤ 1; Тому ймовірність події знаходиться в межах. 0 ≤ Р(А) ≤ 1.
Дії над подіями та їх ймовірностями.
Більш складні випадкові події можна представити, як набір декількох більш простих. Наприклад, випадіння парного числа очок на гральній кості (подія А) може бути представлено, як набір подій А А А А Для представлення складної події через більш прості вводять поняття додавання та множення подій. Сумою (об’єднанням) двох подій А і В називають подію С, яка полягає в здійсненні хоча б однієї з подій А або В (рис. 1). Символічний запис: С = А + В або С = А Добутком (перетином) двох подій А і В називають подію С, яка полягає в одночасному здійсненні події А, і події В (рис. 2). Символічний запис: С = А · В або С = А Ймовірності добутку й суми подій встановлюють за допомогою відповідних теорем.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.161.222 (0.014 с.) |












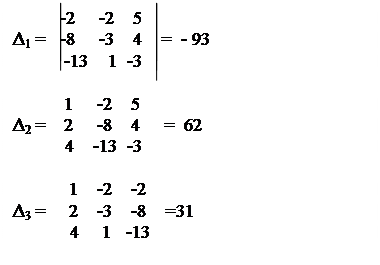












 .
. , А
, А  , А
, А  , де
, де В.
В. В.
В.


