
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виробництво харчової продукції»Содержание книги
Поиск на нашем сайте
Методичні рекомендації з предмету “Вища математика” для студентів заочного відділення Спеціальності Виробництво харчової продукції» Розробив викладач: Розглянуто та рекомендовано _____________Сокирко М. О. ЦК фізико-математичних дисциплін «03» вересня2009р. протокол №__ від”___”______2009р. Голова комісії________М.О. Сокирко
м. Рубіжне 2009р.
Пояснювальна записка
Математика – “універсальна мова”, якою люди широко користуються в усіх галузях своєї діяльності. На сучасному етапі роль її у розвитку суспільства різко зросла, а це вимагає поліпшення математичної підготовки всіх спеціалістів, і зокрема молодших. Навчання студентів вищих навчальних закладів першого та другого рівня акредитації математики передбачає: їх загально – культурний розвиток і загальноосвітню підготовку; забезпечення потреб у математиці їх спільної підготовки та майбутньої професійної діяльності. Реалізація цих функцій потребує використання засобів математики для розвитку пізнавальних здібностей студентів, формування їх наукового світогляду, потреб, мотивації діяльності у першу чергу математичному моделюванню процесів і явищ, які мають загальнокультурне і професійне значення. Головною метою даного курсу є формування теоретичної бази знань та вмінь студентів перед вивченням предметів спеціального циклу. Зміст курсу “Вища математика”, як і кожної дисципліни, визначається цілями і завданням його вивчання. Формувати певні властивості особистості з допомогою різних засобів математики можна на різноманітному матеріалі. Розвиток особистості забезпечується, насамперед тими видами діяльності, які виконуються в процесі навчання, а також їх рівнем. Отже, зміст курсу “Вища математика” визначається в основному потребами спеціальної підготовки та професійної діяльності.
ЗМІСТ 1. Пояснювальна записка. 2. Тематичний план. 3. Загальні вимоги до виконання та оформлення контрольної роботи. 4. Методичні рекомендації до контрольних завдань. 5. Таблиця варіантів. 6. Перелік рекомендованої літератури.
Перелік рекомендованої літератури. 1. Барковський В.В., Барковський Н.В. Математика для економістів: Вища математика, ч.1, Н. Національна академія управління, 1997 – 397с. 2. Богололов Н.В. Практические занятия по математике, М: Высшая школа, 1990 – 495с. 3. Гетьманцев В.Д. Лінійна алгебра і лінійне програмування, К: Либідь, 2001 – 256с. 4. Зайцев И.Л. Элементы высшей математики для техникумов, М: Наука, 1974 – 416с. 5. Рудавський Ю,К., Костробій П.П. Лінійна алгебра та аналітична геометрія, Л: Беснид Бит, 2002 – 262 с.
Зміст дисципліни.
Розділ 1. Диференціальне числення функції однієї та багатьох змінних.
Література:
1. Барковcький В. В., Барковський Н.В. Математика для економістів. Вища математика 1.ч.-К.: Національна академія управління, 1997-397с, с199-237.
Методичні рекомендації.
Якщо функція диференційована в кожній точці деякого проміжку, то вона називається диференційованою на цьому проміжку. Механічний зміст похідної Похідна характеризує швидкість зміни функції при зміні аргументу; зокрема: похідна за часом є міра швидкості зміни, застосовувана до найрізноманітніших фізичних величин. Наприклад, миттєва швидкість v нерівномірного прямолінійного руху є похідною від функції, що виражає залежність пройденого шляху S від часу t. S = S(t) – залежність пройденого шляху від часу; v = S'(t) – швидкість прямолінійного руху; a = v'(t) – прискорення прямолінійного руху. Головну лінійну частину приросту функції називають диференціалом цієї функції. Диференціал функції у = f (х) позначають d у або df (х) d у = f1(х) d х Звідси, похідна функції дорівнює відношенню диференціала функції до диференціала незалежної змінної f1 (x) = При дослідженні функції заданої аналітично, важливо визначити її інтервали зростання, спадання, опуклість графіка функції. Для знаходження інтервалів монотонності заданої функції у = f (х) доцільно дотримуватись такого порядку: 1) знайти похідну f1 (х); 2) знайти корені рівняння f1 (х) =0; 3) визначити знак похідної f 1 (х) в кожному із інтервалів на які поділяється область існування функції f (х) знайденими коренями рівняння f 1 (х) = 0; 4) за одержаними знаками похідної зробити висновок в якому інтервалі функція зростає, а в якому спадає. Щоб визначити, в яких критичних точках функція має екстремум, треба застосувати достатні умови існування екстремуму і дослідити функцію на екстремум за схемою: 1) знайти похідну функції f1 (х); 2)знайти критичні точки першого роду; 3)визначить знак f1 (х) в околі кожної критичної точки; 4)зробити висновок, чи має функція екстремум у знайдених точках і який саме; 5)обчислюють екстремальні значення функції в точках екстремуму. Для науково обґрунтованого дослідження функції та побудови її графіка доцільно дотримуватись такої схеми: 1) Знайти область визначення функції, точки розриву, інтервали неперервності. 2) Дослідити функцію на парність чи непарність, періодичність. 3) Знайти асимптоти графіка функції. 4) Знайти точки перетину графіка функції з осями координат. 5) Знайти критичні точки першого роду, інтервали зростання та спадання функції, точки екстремумів та екстремальні значення функції. 6) Знайти критичні точки другого роду, інтервали опуклості та угнутості графіка функції, точки перегину та значення функції в точках перегину. 7) Згідно з результатами дослідження побудувати у системі координат графік функції.
Питання для самоконтролю.
1. Сформулювати означення похідної функції в точці. 2. Який механічний зміст похідної? 3. Який геометричний зміст похідної? 4. Дайте означення похідної другого порядку функції. 5. Який механічний зміст має похідна другого порядку? 6. Сформулюйте основні правила диференціювання. 7. Дайте означення диференціала функції. 8. Сформулюйте ознаку зростання (спадання) функції. 9. Сформулюйте необхідну і достатню умови існування екстремуму функції. 10. Наведіть схему дослідження функції на екстремум. 11. Сформулюйте необхідну і достатню умови існування точок перегину графіка функції.
Методичні рекомендації.
Первісною функцією для заданої функції f (х) називають таку функцію F(x), похідна якої дорівнює f (х), або диференціал якої дорівнює f (х)dx. Первісна функція F (x) для заданої функції f (х) задовольняє рівності F1 (x) = f (x) або dF (x) = f (x)dx. Сукупність усіх первісних F(x) + C для заданої функції f (х) називають невизначеним інтегралом і позначають ∫f (х) dx. Отже, ∫ f (х) dx = F (x) +C Основні (табличні) інтеграли грають важливу роль в інтегральному численні, тому їх треба запам’ятати. Найбільш часто для знаходження заданого невизначеного інтеграла використовують методи: безпосереднього інтегруванні, заміни змінної (підстановки), інтегрування частинами. Якщо існує скінчена границя інтегральної суми при max ∆ хк → 0, не залежна від способу ділення відрізна [a; в] на частини та добору точок k, то ця границя називається визначеними інтегралом від функції f (х) на відрізку [a, в] і позначається Із означення визначеного інтеграла та основних теорем про границі випливають властивості визначеного інтеграла, які слід застосовувати при обчисленнях інтегралів. Визначений інтеграл застосовують для обчислення площі криволінійної трапеції, обмеженої лініями у = f (х); х = а, х = в за формулою S = Звичайними диференціальними рівняннями називають такі рівняння, які містять шукану функцію однієї змінної та її похідні або диференціали.
х = х0 Загальний розв’язок диференціального рівняння має вигляд у = (х1 С1, С2, …, Сn) або Ф (х1 у1 С1, С2 …, Сn) = 0 Розв’язок Ф (х1 у1 С1, С2, …, Сn) = 0 називають загальним інтегралом диференціального рівняння. Диференціальне рівняння першого роду вигляду N (x) dx + M (у) dу = 0 називають рівнянням з відокремленими змінними. Загальний розв’язок рівняння з відокремленими змінними знаходять за формулою ∫N (x) dx + ∫ M (у) dу =C тобто шляхом його інтегрування. Однорідним диференціальним рівнянням першого порядку називають рівняння, яке можна звести до вигляду у1 = f (х, у), де функція f (х, у) не змінюється при заміні х та у на tx та tу, тобто задовольняє умову f (tx tу) = f (х, у) Однорідне диференціальне рівняння першого порядку шляхом підставки U = можна звести до рівняння з відокремлюваними змінними.
Питання для самоконтролю.
1. Сформулюйте означення первісної функції у = f (х). 2. Назвіть властивості первісної. 3. Дати означення невизначеного інтеграла. 4. Наведіть основні властивості невизначеного інтеграла. 5. Сформулюйте основні правила інтегрування. 6. Які методи інтегрування існують? 7. Сформулюйте означення визначеного інтеграла. 8. Які властивості має визначений інтеграл? 9. Як за допомогою визначеного інтеграла обчислити площу фігури? 10. Як визначають диференціальне рівняння? 11. Сформулюйте означення задачі Коші. 12. Який розв’язок диференціального рівняння називають загальними? 13. Який вигляд має рівняння з відокремленими змінними і як знаходять його загальний розв’язок? 14. Як знайти розв’язок задачі Коші?
Методичні рекомендації. Матриця – таблиця упорядкованих чисел або будь – яких інших об’єктів.
а11 а12 ………. а1n А = а21 а22 ……. а2n ………………….. аm1 am2 ……. amn
Матрицю називають квадратною порядку n, якщо кількість її рядків однакова з кількістю стовпців і дорівнює n. Наступні дії з матрицею: - добуток матриці А на число k:
ka11 ka12 …… ka1n kА = ka21 ka22 ……. ka2n ………………………. kam1 kam2 ……. kamn
- алгебраїчною сумою матриць А та В одного розміру m. n називається матриця С розміру m х n A ± B = С
a11 a12 …… am b11 b12 ……bm a11 ±b11 a12 ± b12.. a1 n±b1n А = a21 a22 ……. a2n; B = b21 b22 …… b2n ; С = a21 ± b21 a22 ± b22 .. a2n ± b2n ………………… ………………….. …………………………… am1 am2 …… amn bm1 bm2 …… bmn am1 ± bm1 am2 ± bm2.. amn ± bmn
- добутком АВ матриці А розміру m х n і матриці В розміром n х р називається матриця С розміром m х р.
Визначником n –го порядку квадратної числової матриці А порядку n називають число, яке знаходиться з елементів матриці А за певним правилом і позначають │А │або ∆ (А). Рангом матриці називають найбільший порядок її мінорів, відмінних від нуля. r (А) = r. Матриця А –1 називається оберненою матрицією до матриці А, якщо виконуються рівності. АА-1 = А-1 А = Е
Матриця А – квадратна, її визначних │А │≠ 0
Система алгебраїчних рівнянь називається лінійною, якщо вона може бути записана у вигляді Де х1, х2, ……, хn – невідомі; аij – дійсне числа, які називають коефіцієнти системи; bk (k = 1.2. ….. m) – вільні члени або їх називають правими частинами рівнянь. Якщо, bk = 0 для усіх k = 1,2, …., m, тоді систему називають однорідною. Якщо хоч би один вільний член bk не дорівнює нулю, тоді система алгебраїчних рівнянь називається неоднорідною.
Розв’язком системи називається множина дійсних чисел α1, α2 ….., αn, підстановка яких у систему замість невідомих х1, х2, …., хn, перетворює кожне рівняння систем у тотожність. Система лінійних алгебраїчних рівнянь, що має хоч би один розв’язок, називається сумісною, а система, що не має розв’язку, називається несумісною. Методи розв’язання систем лінійних алгебраїчних рівнянь: 1) Правило Крамера. Якщо основний визначник ∆ (А) неоднорідної системи n лінійних алгебраїчних рівнянь з n невідомими не дорівнює нулю, то система має єдиний розв’язок, який знаходиться за формулами.
∆к
хк = ∆(А), к = 1,2, ….,n де ∆к - допоміжний визначник, який одержується з основного визначника ∆ (А) шляхом заміни його к –го стовпця, стовпцем вільних членів системи. 2) Матричний метод. Систему лінійних алгебраїчних рівнянь можна записати у матричній формі: А Х = В. Якщо матриця А квадратна порядку n і її визначних ∆(А) не дорівнюю нулю, тоді існує обернена до А матриця А-1. Одержуємо формулу: Х = А-1В за якою знаходять розв’язок системи матричним методом. 3) Метод Гаусса. Система лінійних рівнянь розв’язувається методом послідовного виконання невідомих. Метод послідовного виконання невідомих полягає в тому, що систему алгебраїчних рівнянь зводять до еквівалентної їй трикутної системи, а з утвореної трикутної системи невідомі знаходять послідовними підстановками. 3) Метод Гаусса – Жордана. Число рівнянь m і число n невідомих хj може бути довільними. Метод послідовного виключено невідомих з усіх рівнянь системи, крім одного, називають методом Гаусса – Жордана. Цей метод є деякою модифікацією метода Гаусса. Питання для самоконтролю. 1. Дати означення матриці та її розміру. Які існують рівновиди матриць? 2. Які елементи утворюють головну та неголовну діагоналі матриці? 3. За якими правилами матрицю помножують на дійсне число, знаходять алгебраїчну суму матриць, добуток матриць? 4. Дати означення визначника, за якими правилами обчислюють визначники 2,3 та n – го порядків? 5. Як визначають і знаходять мінор та алгебраїчне доповнення елемента аij матриці А? 6. Сформулюйте властивості визначника. 7. Дати означення рангу матриці та вказати методи його знаходження. 8. Як визначають та позначають обернену матрицю до матриці А? 9. При яких умовах існує обернена матриця? 10. Дати означення системи лінійних алгебраїчних рівнянь. 11. Яка система лінійних алгебраїчних рівнянь називається сумісною? 12. Сформулюйте правило Крамера. 13. Наведіть алгоритм розв’язування системи лінійних алгебраїчних рівнянь матричним методом. 14. У яких випадках система лінійних алгебраїчних рівнянь має нескінчену кількість розв’язків? 15. Сформулюйте алгоритм кроку перетворення Гаусса Жордана. 16. Дати означення базису. 17. Які вектора називаються лінійно незалежними?
Методичні рекомендації. Теорія ймовірностей вивчає закономірності у випадкових подіях. Основними поняттями теорії ймовірності є випробування і події. Під випробуванням (дослідом) розуміють реалізацію комплексу умов, внаслідок якого неодмінно відбудеться яка-небудь подія. Наприклад: кидання монети – випробування; поява герба чи цифри – події. Випадковою подією називають подію, пов’язану з даним випробуванням, яка при здійсненні випробування може відбутися, а може й не відбутися. Слово “випадкова” для стислості часто опускають і говорять просто подія. Наприклад, постріл по цілі – це дослід, випадкові події у цьому досліді – попадання в ціль або промах. Подія називається вірогідною, якщо в результаті досліду вона обов’язково відбудеться і неможливою, якщо вона не може відбутися. Наприклад: випадання не більше шести очків при киданні однієї гральної кості – вірогідна подія; випадання десяти очок при киданні однієї гральної кості – неможлива подія. Події називаються несумісними, якщо ніякі дві з них не можуть відбутись одночасно. Наприклад: попадання і промах при одному пострілі – це несумісні події. Говорять, що декілька подій у даному досліді утворюють повну систему подій, якщо в результаті досліду неодмінно повинно відбутися хоча б одна з них. Наприклад: при киданні гральної кості події, які полягають у випаданні одного, двох, трьох, чотирьох, п’яти і шести очок, утворюють повну систему подій. Події називають рівноможливими, якщо ні одна з них не є об’єктивно більш можлива, ніж інша. Наприклад при киданні монети випадання герба чи числа – події рівно можливі. Кожна подія має якусь степінь можливості. Числова міра степеня об’єктивної можливості події – це ймовірність події. Ймовірність події А позначається Р(А). Нехай з системи n- несумісних рівно можливих наслідків випробувань m- наслідків сприяють події А. Тоді ймовірність події А обчислюється по формулі:
Р(А) =
Ця формула носить назву класичного означення ймовірності. Якщо В – вірогідна подія, то m = n, отже Р(В) = 1; Якщо С – неможлива подія, то m = 0, отже Р(С) = 0; Якщо А – вірогідна подія, то m ≤ n, отже Р(А) ≤ 1; Тому ймовірність події знаходиться в межах. 0 ≤ Р(А) ≤ 1.
Дії над подіями та їх ймовірностями.
Більш складні випадкові події можна представити, як набір декількох більш простих. Наприклад, випадіння парного числа очок на гральній кості (подія А) може бути представлено, як набір подій А А А А Для представлення складної події через більш прості вводять поняття додавання та множення подій. Сумою (об’єднанням) двох подій А і В називають подію С, яка полягає в здійсненні хоча б однієї з подій А або В (рис. 1). Символічний запис: С = А + В або С = А Добутком (перетином) двох подій А і В називають подію С, яка полягає в одночасному здійсненні події А, і події В (рис. 2). Символічний запис: С = А · В або С = А Ймовірності добутку й суми подій встановлюють за допомогою відповідних теорем. Формула Бернуллі.
Нехай відбувається n незалежних випробувань, в кожному з яких ймовірність того, що відбудеться подія А рівна p. Тоді ймовірність того, що при n випробуваннях подія А відбудеться рівно k обчислюється за формулою Бернуллі. Р
Дійсно, випадок, коли подія А відбудеться в кожному з перших випробувань, і не відбудеться в інших n- k випробуваннях можна представити як добуток подій А і
Згідно умови, всі випробування незалежні, тому Р Подія А може відбутись k раз привипробуваннях і в іншій послідовності, наприклад
але ймовірність залишиться незмінною, бо від перестановки множників добуток не змінюється. Число всіх можливих послідовностей, в яких відбуватимуться події А і рівне С Питання для самоконтролю. 1. Чим займається теорія ймовірностей як математична наука? 2. Навести приклади випадкових подій, масових випадкових подій. 3. Які поняття теорії ймовірностей приймаються за первісні не означувані поняття? 4. Яка подія називається випадковою? 5. Які випадкові події називаються масовими? 6. Які події називаються попарно несумісними? 7. Які сукупності подій утворюють повну групу? 8. Які події називаються елементарними? 9. Сформулюйте класичне означення ймовірності події. 10. Чому дорівнює ймовірність вірогідної і неможливої події? 11. Сформулюйте принцип практичної впевненості. 12. Яка подія називається складною? 13. Що називається сумою подій? 14. Сформулюйте теорему додавання ймовірностей подій і наслідки з неї. 15. Які події називаються протилежними? 16. Що називається добутком подій? 17. Сформулюйте теорему множення ймовірностей незалежних подій. 18. Які випробування називаються взаємно незалежними? 19. Що називається статистичною частотою події? 20. Сформулюйте статистичне означення ймовірності. 21. Сформулюйте теорему Бернуллі.
Завдання для контрольної роботи. Застосування похідної
1. Побудувати графік функції у=х3–3х–2 2. Резервуар ємкістю 108 м3 з квадратною основою, відкритий зверху, треба покрити емаллю. Які повинні бути розміри резервуару, щоб витратити для цього мінімальну кількість емалі. 3. Побудувати графік функції у = 1/ 8 х3 – х2 + 1 4. Тіло рухається прямолінійно за законом S= – 12t + 2t2 + 1/3 t3. Знайдіть найбільшу швидкість руху тіла. 5. Які розміри повинен мати циліндр, площа повної поверхні якого см2, щоб його об’єм був найбільшим. 6. Шлях S в метрах, пройдений тілом заt секунд при прямолінійному русі, визначається рівнянням S= 1/3 t3–t2+2 t–1. Знайдіть швидкість та прискорення в кінці третьої секунди. 7. Доведіть, що з усіх прямокутників, що мають периметр 32 см, найбільшу площу має квадрат. 8. Знайдіть найбільше та найменше значення функції у=х5–5х4+5х3+1 на відрізку 1 9. Побудуйте графік функції у = х3–3х2 10. Число 50 представте в вигляді суми двох додатних додатків так, щоб добуток цих чисел був найбільшим. 11. Скласти рівняння дотичної до графіка функції у = х3 + 2х2 – 4х – 3 в точці з абсцисою х = -2. 12. Побудуйте графік функції у = х3 – 2х2 + х. 13. Треба виготовити ящик з кришкою, об’єм якого дорівнює 228 см3, а сторони основи відносяться як 1: 3. Які повинні бути розміри ящика, щоб його повна поверхня була найменшою? 14. Навкруг стіни треба зробити забор, щоб огородити прямокутну ділянку землі найбільшої площі. Загальна довжина забору 60 м. Знайти довжину частини забору паралельно стіні. 15. Знайти найбільше та найменше значення функції у = х4– 2х2 + 5 на відрізку – 2 < x <2. 16. Гіпотенуза прямокутного трикутника дорівнює 8 см. Знайти довжину кожного катета, якщо площа трикутника повинна бути найбільшою. 17. Напишіть рівняння дотичних до кривої у = х3 + 2х2 – 3х в точках її перетину з віссю Ох. 18. Докажіть, що з усіх прямокутників з площею 400 см2 квадрат має найменший периметр. 19. Знайти найбільше та найменше значення функції у = х3 – 3х2 + 3х + 2 на відрізку 2 < x < 5. 20. Побудуйте графік функції у = 3х – х3. 21. Число 25 запишіть в вигляді добутку двох додатних чисел, сума яких найменша. 22. Напишіть рівняння дотичних до графіка функції q (х) = 23. Який з рівнобедрених трикутників з периметром 2р має найбільшу площу?
24. З усіх прямокутних паралелепіпедів, в яких в основі лежить квадрат і площа повної поверхні дорівнює 600 см2, знайти паралелепіпед найбільшого об’єму та визначити його розміри. 25. Побудувати графік функції у = 2х3 – 3х2.
ТАБЛИЦЯ ВАРІАНТІВ
Методичні рекомендації з предмету “Вища математика” для студентів заочного відділення Спеціальності Виробництво харчової продукції» Розробив викладач: Розглянуто та рекомендовано _____________Сокирко М. О. ЦК фізико-математичних дисциплін «03» вересня2009р. протокол №__ від”___”______2009р. Голова комісії________М.О. Сокирко
м. Рубіжне 2009р.
Пояснювальна записка
Математика – “універсальна мова”, якою люди широко користуються в усіх галузях своєї діяльності. На сучасному етапі роль її у розвитку суспільства різко зросла, а це вимагає поліпшення математичної підготовки всіх спеціалістів, і зокрема молодших. Навчання студентів вищих навчальних закладів першого та другого рівня акредитації математики передбачає: їх загально – культурний розвиток і загальноосвітню підготовку; забезпечення потреб у математиці їх спільної підготовки та майбутньої професійної діяльності. Реалізація цих функцій потребує використання засобів математики для розвитку пізнавальних здібностей студентів, формування їх наукового світогляду, потреб, мотивації діяльності у першу чергу математичному моделюванню процесів і явищ, які мають загальнокультурне і професійне значення. Головною метою даного курсу є формування теоретичної бази знань та вмінь студентів перед вивченням предметів спеціального циклу. Зміст курсу “Вища математика”, як і кожної дисципліни, визначається цілями і завданням його вивчання. Формувати певні властивості особистості з допомогою різних засобів математики можна на різноманітному матеріалі. Розвиток особистості забезпечується, насамперед тими видами діяльності, які виконуються в процесі навчання, а також їх рівнем. Отже, зміст курсу “Вища математика” визначається в основному потребами спеціальної підготовки та професійної діяльності.
ЗМІСТ 1. Пояснювальна записка. 2. Тематичний план. 3. Загальні вимоги до виконання та оформлення контрольної роботи. 4. Методичні рекомендації до контрольних завдань. 5. Таблиця варіантів. 6. Перелік рекомендованої літератури.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.02 с.) |

 Похідною функції
Похідною функції  в точці
в точці  називається границя відношення приросту функції в точці х до приросту аргументу, коли приріст аргументу прямує до нуля. Це число позначається через
називається границя відношення приросту функції в точці х до приросту аргументу, коли приріст аргументу прямує до нуля. Це число позначається через  або у'. Функцію, яка має похідну в точці
або у'. Функцію, яка має похідну в точці  .
.
 f (х) dx
f (х) dx Сумісні завдання диференціального рівняння та відповідної кількості початкових умов називають задачею Коші: F (x, у, у1) = 0
Сумісні завдання диференціального рівняння та відповідної кількості початкових умов називають задачею Коші: F (x, у, у1) = 0 у =у0
у =у0











 .
.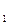 , А
, А  , А
, А  , де
, де В.
В. В.
В. (k)=С
(k)=С  р
р  (1- р)
(1- р) 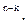
 :
:



 .
.
 в точці х0=2.
в точці х0=2.


