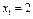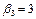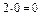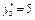Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади розв’язування задач динамічного програмуванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приклад 9.1. Фірма планує нарощувати виробничі потужності на чотирьох підприємствах, маючи для цього 4 млн грн. Для кожного з підприємств розроблено інвестиційні проекти, які відбивають прогнозовані сумарні витрати С та доходи D, пов’язані з реалізацією кожного проекту. Зміст цих проектів ілюструє таблиця:
Перший проект передбачає відмовитися від розширення підприємства, а тому має нульові витрати і доходи. Розробити план інвестування виділених коштів у зазначені підприємства так, щоб одержати максимальний прибуток. Розв’язування. Спрощеним і найменш ефективним способом розв’язування таких задач є перебір усіх можливих варіантів. Проте на практиці їх так багато, що проаналізувати всі і вибрати серед них найефективніший неможливо. Головними недоліками такого способу розв’язування є великий обсяг обчислень, відсутність апріорної інформації про неприпустимі розв’язки, а також неможливість скористатися проміжними результатами аналізу для відкидання неоптимальних комбінацій проектів. Розв’яжемо цю задачу за алгоритмом (методом) зворотного прогону. Кроками задачі вважатимемо кожне з чотирьох підприємств, оскільки для кожного з них маємо вибрати оптимальний інвестиційний проект за обмежених грошових ресурсів. Зауважимо, що в цьому разі нединамічний процес розглядаємо як динамічний, аби скористатися методами динамічного програмування для знаходження оптимального розв’язку. Зв’язок між зазначеними кроками забезпечується обмеженнями на загальний обсяг виділених коштів — 4 млн грн. Змінні задачі візьмемо так, щоб послідовно керувати процесом розподілу коштів:
Рекурентне співвідношення для зворотного прогону від кроку 4-го до 1-го (від четвертого підприємства до першого) подається у вигляді:
де Тут Виконаємо поетапні розрахунки за цією моделлю. Етап 4.
Результати розрахунків подамо таблицею:
Етап 3.
за умов
Результати розрахунків відбиває таблиця:
Розрахунки виконуються так. Нехай потрібно знайти
Отже,
Зауважимо, що
Етап 2.
за умов
Результати розрахунків подаємо таблицею:
Етап 1.
за умов
Виконуємо розрахунки лише для х 1 = 4, подаючи їх у вигляді таблиці:
Знайдемо оптимальний план. Із таблиці першого кроку випливає, що
Приклад 9.2. Підприємство розробляє стратегію поповнення запасів деякої продукції для заданого періоду часу, який складається з N етапів (підперіодів). Для кожного з них відомий розмір попиту, причому він не є однаковим для всіх етапів. Щоб задовольнити попит, підприємство може придбати необхідну кількість продукції, замовивши її у виробника, або виготовити її самостійно. Передбачається, що запаси поповнюються миттєво, запізнення поставки та дефіцит неприпустимі. Залежно від ринкової кон’юнктури підприємству може бути вигідно створювати запаси продукції для задоволення попиту в майбутні періоди часу, що пов’язано, проте, з додатковими витратами на зберігання запасів. Розробити програму управління запасами підприємства, тобто визначити обсяги замовлення й період його розміщення, щоб загальні витрати на постачання та зберігання продукції були мінімальними, а попит задовольнявся повністю й своєчасно. Дані задачі наведено в таблиці:
Відомо, що на початку планового періоду запас становить 2 тис. од., а під час купівлі продукції діє система оптових знижок. Витрати на придбання 1 тис. од. продукції становлять 15 тис. грн., а коли розмір замовлення перевищує 3 тис. од., витрати знижуються на 12% і становлять 12 тис. грн. Нехай Визначимо f (xi, yi) як мінімальні витрати на етапах Рекурентні залежності, що відповідають схемі зворотного прогону, набирають вигляду:
за умов
Для N -го етапу маємо:
за умов
Розглянемо покроковий розрахунок оптимальної стратегії управління запасами. Етап 4. Маємо
за умов
Можливі варіанти розв’язків ілюструє таблиця:
Етап 3. Маємо
за умов
Результати розрахунків подамо у вигляді таблиці:
Розрахунки виконуємо так. Наприклад, обчислимо
Аналогічно:
Далі обчислюємо:
Отже, Так само виконуємо розрахунки для х = 1, 2, 3, 4, 5, а результати вміщуємо у відповідну таблицю. Етап 2. У таблицю записуємо лише остаточні результати: Маємо b3 = 5.
за умов
Етап 1. Діємо так, як і на етапі 2, складаючи таблицю результатів:
Маємо b1 = 4.
за умов
Отже, дістали два оптимальні плани управління запасами підприємства, яким відповідають мінімальні сумарні витрати на постачання та зберігання продукції. Інформацію про перший оптимальний план містить таблиця:
Інформація про другий оптимальний план:
Порівнюючи ці два плани, бачимо, що відрізняються вони першими двома етапами і дають можливість маневрувати фінансовими ресурсами підприємства, що водночас вирішує ще низку проблем. 9.2 Приклади та завдання для самостійної роботи 9.1 Фірма планує нарощувати виробничі потужності на трьох підприємствах, виділяючи для цього 18 млн грн. За кожним із підприємств розроблено інвестиційний проект із зазначенням прогнозованих сумарних витрат С та доходів D, що пов’язані з його реалізацією. Розробити план інвестування.
9.2 Розв’язати попередню задачу (9.1), якщо розмір інвестицій становить 20 млн грн., а перший інвестиційний проект (ситуація, коли певному підприємству не виділяється коштів) є неприпустимим. 9.3 Розв’язати задачу 9.1, якщо модернізація має проводитися ще на одному — четвертому підприємстві фірми, для якого розроблено три інвестиційні проекти:
Врахувати, що інвестиційний портфель збільшиться на 2 млрд грн. 9.4 Знайти оптимальний розподіл 6 млрд грн. між трьома підприємствами галузі. Прибуток, який можна одержати від капіталовкладень певного розміру в кожне з підприємств, відбиває таблиця:
9.5 Розв’язати задачу оптимального розподілу капіталовкладень між чотирма підприємствами, якщо загальний розмір інвестицій становить 12 млн грн. Вихідні дані вміщено в таблиці:
9.6 Розв’язати чотириетапну задачу управління запасами за вихідними даними:
Відомо, що витрати на зберігання одиниці продукції протягом одного етапу сталі і становлять 2 грн., витрати на придбання одиниці продукції — 3 грн. для всіх етапів. Вихідний запас на початок досліджуваного періоду — 10 од.
9.7 Розв’язати попередню задачу, якщо вихідний запас дорівнює 40 од., а витрати на зберігання змінюються поетапно і становлять відповідно 1; 1,5; 2; 5 грн. 9.8 Розв’язати п’ятиетапну детерміновану задачу управління запасами:
Функція витрат на розміщення замовлення визначає питомі витрати: 20 грн. для перших 50 од. та 10 грн. за кожну додаткову одиницю (знижка на кількість). 9.9 Розв’язати на ПК десятиетапну детерміновану задачу управління запасами, вважаючи, що вихідний запас дорівнює 65 од.
9.10. Розв’язати задачу, розв’язок якої наведено в прикладі 9.1, якщо розмір інвестицій становить 10 млн грн., а перший інвестиційний проект має наступні характеристики
ТЕОРІЯ ІГОР
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 768; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.017 с.) |






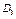
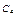

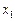 — обсяг капіталовкладень, виділених на кроках 1—4;
— обсяг капіталовкладень, виділених на кроках 1—4; — те саме на кроках 2—4;
— те саме на кроках 2—4; — те саме на кроках 3 і 4;
— те саме на кроках 3 і 4; — те саме на кроці 4.
— те саме на кроці 4.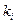
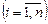 — обсяги інвестицій на і- му підприємстві
— обсяги інвестицій на і- му підприємстві  .
.
 — оптимальні обсяги інвестицій на і -му підприємстві.
— оптимальні обсяги інвестицій на і -му підприємстві. ,
,
 ,
,  ,
, — сумарна ефективність інвестицій з і -го кроку до останнього.
— сумарна ефективність інвестицій з і -го кроку до останнього. , оскільки п’ятого підприємства не існує.
, оскільки п’ятого підприємства не існує. .
.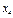







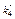

 ,
, 






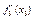









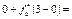




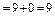
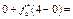





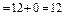
 . Обчислюємо
. Обчислюємо .
. ,
,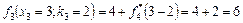 ,
, .
. , оскільки для третього підприємства не існує проекту з інвестиціями в 1 млн грн. Значення
, оскільки для третього підприємства не існує проекту з інвестиціями в 1 млн грн. Значення  беремо з попередньої таблиці. Далі маємо:
беремо з попередньої таблиці. Далі маємо: .
.
 ,
, 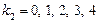 .
.








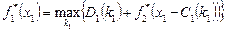
 ,
,  .
.






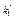

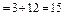




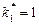 , тобто для першого підприємства реалізується другий проект, який використовує 1 млн грн. інвестицій з ефективністю 3 млн грн. Отже, для другого, третього і четвертого підприємств залишається 4 – 1 = 3 млн грн. інвестицій. Із таблиці другого кроку маємо, що за умов х 2 = 3 максимальний ефект настає в разі реалізації для другого підприємства першого проекту (k 2 = 1), ефективність становить 4 млн грн. Отже, х 3 = 3 – 1 = 2, тобто для третього і четвертого підприємств слід використати 2 млн грн. інвестицій. Із таблиці третього кроку за умов х 3 = 2 маємо, що k 3 = 0. Отже, х 4 = 2, а йому відповідають капітальні вкладення k 4 = 2, ефективність яких 8 млн грн. Остаточно маємо: ефективність 4 млн грн. інвестицій становить 3 + 4 + 8 = 15 (млн грн.).
, тобто для першого підприємства реалізується другий проект, який використовує 1 млн грн. інвестицій з ефективністю 3 млн грн. Отже, для другого, третього і четвертого підприємств залишається 4 – 1 = 3 млн грн. інвестицій. Із таблиці другого кроку маємо, що за умов х 2 = 3 максимальний ефект настає в разі реалізації для другого підприємства першого проекту (k 2 = 1), ефективність становить 4 млн грн. Отже, х 3 = 3 – 1 = 2, тобто для третього і четвертого підприємств слід використати 2 млн грн. інвестицій. Із таблиці третього кроку за умов х 3 = 2 маємо, що k 3 = 0. Отже, х 4 = 2, а йому відповідають капітальні вкладення k 4 = 2, ефективність яких 8 млн грн. Остаточно маємо: ефективність 4 млн грн. інвестицій становить 3 + 4 + 8 = 15 (млн грн.). — кількість етапів планового періоду. Тоді для і -го етапу застосуємо такі позначення: хі — запас продукції на початок етапу; yi — обсяг замовленої продукції (розмір замовлення); hi — витрати на зберігання 1 тис. од. продукції запасу; kі — витрати на розміщення замовлення;
— кількість етапів планового періоду. Тоді для і -го етапу застосуємо такі позначення: хі — запас продукції на початок етапу; yi — обсяг замовленої продукції (розмір замовлення); hi — витрати на зберігання 1 тис. од. продукції запасу; kі — витрати на розміщення замовлення;  — попит на продукцію; Ciyi — витрати, що пов’язані із купівлею (виробництвом) продукції yi.
— попит на продукцію; Ciyi — витрати, що пов’язані із купівлею (виробництвом) продукції yi. , якщо рівень запасів хі.
, якщо рівень запасів хі.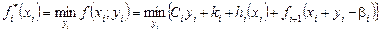
 ,
,  ,
,  .
.
 ,
,  .
.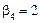

 .
.











 .
.











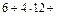



















 і
і  . Оскільки за умовою
. Оскільки за умовою  , то
, то  може набувати значень 0, 1, 2, 3, 4, 5, а
може набувати значень 0, 1, 2, 3, 4, 5, а  — відповідно значень 0, 1, 2, 3, 4, 5. Тепер знайдемо
— відповідно значень 0, 1, 2, 3, 4, 5. Тепер знайдемо  для
для  і
і  . Для
. Для  маємо:
маємо: .
. ,
, .
.
 при
при  .
.
 .
.









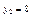





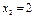





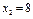

















 .
.