
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція 7. Олімпіадні задачі та їх особливостіСодержание книги Поиск на нашем сайте
Розвиток системи освіти в Україні на сучасному етапі передбачає переорієнтацію процесу навчання на розвиток особистості учня, розкриття його творчого потенціалу. Одним із засобів розвитку творчих здібностей учнів є підготовка їх до участі в олімпіадах з фізики. Для виконання олімпіадних завдань учні повинні володіти певним обсягом теоретичних знань, вищим, ніж середній рівень. Щоб допомогти учням в оволодінні навичками розв'язування нестандартних задач, треба визначити особливості олімпіадних задач відносно типових програмних задач та ознайомити учнів зі способами розв'язування таких задач. Виділимо кілька напрямів, які визначають складність олімпіадних задач порівняно з типовими задачами: а) ускладнення за рахунок збільшення числа взаємодіючих об'єктів, якщо зберігається природа явища (наприклад, збільшення числа рухомих взаємозв'язаних тіл у механічному русі, збільшення числа резисторів, конденсаторів, джерел струму в колі постійного струму та ін.); б) ускладнення за рахунок об'єднання в одній фізичній ситуації кількох окремих випадків даного фізичного явища (наприклад, об'єднання в одній фізичній ситуації різного виду рівноприскорених рухів — з початковою швидкістю, без початкової швидкості, рівноприскорених рухів взаємозв'язаних тіл у різних напрямах та ін.); в) ускладнення за рахунок об'єднання в одній фізичній ситуації суміжних фізичних явищ різної природи (наприклад, механічних і теплових, електричних і механічних тощо); г) ускладнення за рахунок задання вихідних даних у різній формі (наприклад, кількісні міри результатів взаємодії об'єктів треба встановити на підставі графічної чи образної інформації); г) ускладнення за рахунок представлення у фізичній ситуації взаємнопротилежних процесів, так що кінцевий результат залежить від того, який із процесів переважає; д) ускладнення, пов’язане з невизначеністю умов задачі (наприклад, вихідні дані задані нечітко, і для їх уточнення треба попередньо проаналізувати ситуацію задачі). Розв'язування задач певного виду складності потребує від учнів певних умінь і навичок. Так, розв'язування задач зі збільшеною кількістю взаємодіючих об'єктів пов'язане з громіздкими математичними обчисленнями та перетвореннями і потребує від учня, крім доброї математичної підготовки, уміння концентрувати протягом тривалого часу увагу на обчисленнях, уміння здійснювати самоконтроль правильності виконуваних дій. Розв'язування задач із представленням у певній фізичній ситуації різних фізичних явищ чи їх випадків потребує від учня вміння розпізнавати й моделювати фізичні явища. Розв'язування задач із різною формою задання вихідних даних потребує вміння перетворювати якісні характеристики об'єктів у кількісні, тобто вміння підбирати для опису стану об'єктів певні фізичні величини та їх числові значення. І, нарешті, розв'язування задач із невизначеними умовами потребує вміння оцінювати різні варіанти розвитку фізичної взаємодії залежно від можливої зміни вихідних даних. Для успішного розв'язування олімпіадних задач учень повинен не лише володіти загальними мислительними вміннями і навичками, а й бути знайомим зі спеціальними прийомами, які використовуються у професійних фізичних дослідженнях. До них належать: • вибір системи відліку, в якій рух матиме простіший вигляд; • застосування методу оборотності для переформулювання умов прямої задачі на зворотну; • застосування теореми Варіньйона для знаходження центра мас; • застосування методу моделювання; • застосування методу еквіпотенціальних вузлів, а також методу виключення ділянок; • застосування методу дзеркальних відображень. Застосування будь-якого з цих прийомів виправдане лише в тому разі, коли звичайними методами задача не піддається розв'язанню, чи коли застосування спеціального прийому дає значний виграш у часі. Як приклад розглянемо задачу. Задача. Два спортсмени-гребці, які весь час гребуть з однаковою силою, пливуть на човнах: перший — за течією річки, другий — проти течії. Коли човни розминулися, один зі спортсменів кинув у човен другого естафетну дерев'яну паличку. Спортсмени не помічають, що паличка впала у воду на лінії, де розминулися човни, і продовжують рухатися з такими самими швидкостями. Через 10 хв після цього моменту спортсменам повідомили, що естафетна паличка пливе за течією річки, тому вони змінили напрям руху на протилежний. Яка швидкість течії річки, якщо другий спортсмен може наздогнати естафетну паличку на відстані 2 км від того місця, де човни розминулися? Де зустрінеться з паличкою перший спортсмен? Розв'язування задачі, якщо вибрати традиційну систему відліку, пов'язану із «землею», зводиться до розв'язування системи рівнянь для другого спортсмена.
де t — час від того моменту, як розминулися човни, до моменту виявлення втрати палички; S1 — шлях, який пройшов другий спортсмен за час t, S2 — шлях, який пропливла паличка при власному русі; Таке розв'язування вимагає досить громіздких перетворень. Якщо за систему відліку вибрати естафетну паличку, то паличка і вода не рухаються, а другий спортсмен спочатку віддаляється від палички на відстань S1 за час t, а потім наближається до неї за той самий час. За цей же час паличка пропливе відстань S2. Таким чином, маємо Дослідною перевіркою вибирають типи задач, які викликають значні труднощі. Такий вибір має індивідуальний характер. Задач підбирають якнайбільше, щоб була можливість сформувати в учнів стійкі навички їх розв'язування. Розв'язанню задач має передувати ознайомлення з теоретичним матеріалом у достатньому обсязі. Теоретичні знання можуть даватися в повному обсязі перед розв'язуванням задач певного типу, або в процесі розв'язування задач (як відповіді на запитання, що виникають). Корисно варіювати обидва способи. Треба добиватися, щоб учні впевнено орієнтувалися в теоретичному матеріалі, щоб не створювалися додаткові труднощі для розв'язування задач. На заключних етапах підготовки корисно пропонувати учням задачі без оголошення виду складності, щоб учні могли самостійно проаналізувати особливості задачі та визначити шляхи її розв'язування. За такого підходу до підготовки учні не лише ознайомляться з розв'язуванням нестандартних задач, а й у них будуть формуватися мислительні навички щодо аналізу умови задачі, моделювання фізичної ситуації задачі, побудови плану розв'язування задачі та аналіз знайденого результату. Крім того, в учнів буде нагромаджуватися досвід аналізу та розв'язування типових ситуацій. Це допоможе учневі зекономити час на олімпіаді.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.239.157 (0.006 с.) |

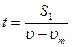 ;
; 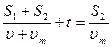
 — швидкість спортсменів,
— швидкість спортсменів, 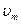 — швидкість течії річки.
— швидкість течії річки. .
.


