
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Економічна інтерпретація двоїстої задачіСодержание книги
Поиск на нашем сайте
Приклади розв’язування навчальних завдань Приклад 4.1. Деяке підприємство виробляє чотири види продукції А, В, С і Д, використовуючи для цього три види ресурсів 1, 2 і 3. Норми витрат ресурсів на одиницю кожної продукції (в умовних одиницях) наведено в таблиці:
Відома ціна одиниці продукції кожного виду: для продукції А — 2 ум. од., для В і Д — по 4 од., для С — 3 од. Визначити оптимальний план виробництва продукції кожного виду в умовах обмеженості ресурсів, який дає підприємству найбільший дохід. Наведемо симплекс-таблицю, що відповідає оптимальному плану поставленої задачі.
Виконаємо зазначені далі дії. 1. Сформулювати математичну модель даної задачі лінійного програмування та двоїстої до неї. 2. Записати оптимальні плани прямої та двоїстої задач і зробити їх економічний аналіз. 3. Визначити статус ресурсів прямої задачі та інтервали стійкості двоїстих оцінок відносно зміни запасів дефіцитних ресурсів. 4. Визначити план виробництва продукції та зміну загального доходу підприємства, якщо запас першого ресурсу збільшити на 10 од., другого — зменшити на 10 од., а третього — збільшити на 20 ум. од. 5. Визначити рентабельність кожного виду продукції, що виготовляється на підприємстві. 6. Розрахувати інтервали можливої зміни ціни одиниці кожного виду продукції. Розв’язування. 1. Математичні моделі прямої та двоїстої задачі мають такий вигляд:
де хj — обсяг виробництва продукції j -го виду
де yi — оцінка одиниці і -го виду ресурсу 2. З наведеної симплекс-таблиці маємо: Х * = (0; 0; 35; 45; 0; 30; 0), max Z = 285; Y * = (4; 0; 3) ∙ min F = 250/2 + 160 = 285 = max Z. Оптимальний план прямої задачі передбачає виробництво лише двох видів продукції С і Д у кількості відповідно 35 та 45 од. Випуск продукції А та В не передбачається (х 1 = х 2 = 0). Додаткові змінні х 5, х 6, х 7 характеризують залишок (невикористану частину) ресурсів відповідно 1, 2 та 3. Оскільки х 6 = 30, другий ресурс використовується у процесі виробництва продукції не повністю, а перший та третій ресурси — повністю (х 5 = х 7 = 0). За такого оптимального плану виробництва продукції та використання ресурсів підприємство отримує найбільший дохід у розмірі 285 ум. од. План двоїстої задачі дає оптимальну систему оцінок ресурсів, що використовуються у виробництві. Так, у 1 = 1/2 та у 3 = 2 відмінні від нуля, а ресурси 1 та 2 використовуються повністю. Двоїста оцінка у 2 = 0 і відповідний вид ресурсу не повністю використовується при оптимальному плані виробництва продукції. Це підтверджується також попереднім аналізом додаткових змінних оптимального плану прямої задачі. Така оптимальна система оцінок дає найменшу загальну вартість усіх ресурсів, що використовуються на підприємстві: min F = 285 ум. од. 3. Статус ресурсів прямої задачі можна визначити трьома способами. Перший — підстановкою Х * у систему обмежень прямої задачі. Якщо обмеження виконується як рівняння, то відповідний ресурс дефіцитний, у противному разі — недефіцитний.
Другий спосіб — за допомогою додаткових змінних прямої задачі. Якщо додаткова змінна в оптимальному плані дорівнює нулю, то відповідний ресурс дефіцитний, а якщо відмінна від нуля — ресурс недефіцитний. Третій спосіб — за допомогою двоїстих оцінок. Якщо уі ¹ 0, то зміна (збільшення або зменшення) обсягів і -го ресурсу приводить до відповідної зміни доходу підприємства, і тому такий ресурс є дефіцитним. Якщо уі = 0, то і -й ресурс недефіцитний. Так, у 1 = 1/2 (ресурс 1 дефіцитний); у 2 = 0 (ресурс 2 недефіцитний); у 3 = 2 (ресурс 3 дефіцитний). Отже, якщо запас першого дефіцитного ресурсу збільшити на одну умовну одиницю (b 1 = 250 + 1 = 251), то цільова функція max Z збільшиться за інших однакових умов на у 1 = 1/2 ум. од. і становитиме max Z = 285,5 ум. од. Але за рахунок яких змін в оптимальному плані виробництва продукції збільшиться дохід підприємства? Інформацію про це дають елементи стовпчика «х 5» останньої симплекс-таблиці, який відповідає двоїстій оцінці у 1 = 1/2. У новому оптимальному плані значення базисної змінної Х * = (0; 0; 34,5; 45,5; 0; 29; 0). Отже, збільшення запасу першого дефіцитного ресурсу за інших однакових умов приводить до зростання випуску продукції Д та падіння виробництва продукції С, а обсяг використання ресурсу 2 збільшується. За такого плану виробництва максимальний дохід підприємства буде max Z = 2 × 0 + 4 × 0 + 3 × 34,5 + 4 × 45,5 = 285,5, тобто зросте на у 1 = 1/2. Проаналізуємо, як зміниться оптимальний план виробництва продукції, якщо запас дефіцитного ресурсу 2 за інших однакових умов збільшити на одну умовну одиницю (b 3 = 80 + 1 = 81). Аналогічно попереднім міркуванням, скориставшись елементами стовпчика «х 7» останньої симплекс-таблиці, що відповідає двоїстій оцінці у3 = 2, можна записати новий оптимальний план: Х * = (0; 0; 37; 44; 0; 30; 0). max Z = 2 × 0 + 4 × 0 + 3 × 37 + 4 × 44 = 287. Отже, дохід підприємства збільшиться на дві умовні одиниці за рахунок збільшення виробництва продукції С на дві одиниці та зменшення випуску продукції Д на одну одиницю. При цьому обсяг використання ресурсу 2 не змінюється. Але після проведеного аналізу постає логічне запитання: а чи зберігатимуться встановлені пропорції, якщо запас дефіцитного ресурсу змінити не на одиницю, а наприклад, на 10 ум. од.? Щоб однозначно відповісти на поставлене запитання, необхідно розрахувати інтервали можливої зміни обсягів дефіцитних ресурсів, у межах яких двоїсті оцінки уі залишаються на рівні оптимальних значень. Приріст (зміну) запасу ресурсу 1 позначимо D b 1. Тоді, якщо Х * = (0; 0; 35–1/2D b 1; 45 + 1/2D b 1; 0; 30 – D b 1; 0). Єдина вимога, яку можна поставити до можливих нових оптимальних значень, — це умова невід’ємності, тобто
Це означає, що коли запас ресурсу 1 збільшиться на 30 ум. од. або зменшиться на 90 ум. од., то оптимальною двоїстою оцінкою ресурсу 1 залишиться у 1 = 1/2. Отже, запас ресурсу 1 може змінюватись у межах
Згідно з цим максимально можливий дохід підприємства перебуватиме в межах
а оптимальний план виробництва продукції (0; 0; 80; 0; 0; 120; 0) ≤ Х * ≤ (0; 0; 20; 60; 0; 0; 0). Аналогічно розраховується інтервал стійкості двоїстої оцінки у 3 = 2 дефіцитного ресурсу 3:
Отже, якщо запас ресурсу 3 збільшиться на 45 ум. од. або зменшиться на 17,5 ум. од., то двоїста оцінка у 3 = 2 цього ресурсу залишиться оптимальною. Згідно із цим можливий дохід підприємства та оптимальний план виробництва продукції перебуватимуть у межах
(0; 0; 0; 62,5; 0; 30; 0) ≤ Х * ≤ (0; 0; 125; 0; 0; 30; 0). Зауважимо, що визначені інтервали стосуються лише випадків, коли змінюється тільки один ресурс, а запаси всіх інших фіксовані, тобто за інших однакових умов. У разі одночасної зміни обсягів усіх або кількох ресурсів підхід до визначення нового оптимального плану дещо інший. 4. За умовою задачі обсяги всіх трьох ресурсів змінюються відповідно D b 1 = +10, D b 2 = –10, D b 3 = +20. Для визначення компонентів нового оптимального плану скористаємось одним із головних співвідношень обчислювальної процедури симплекс-методу:
З останньої симплекс-таблиці можна записати обернену матрицю:
Змінені запаси ресурсів утворюють вектор
Тоді новий оптимальний план виробництва продукції за відповідної одночасної зміни запасів усіх трьох ресурсів
тобто Х * = (0; 0; 70; 30; 0; 10; 0). Усі хj ≥ 0, і тому оптимальним планом двоїстої задачі залишається Y * = (1/2; 0; 2). Загальний максимальний дохід підприємства зміниться на ∆ Z max = D b 1 y 1 + D b 2 y 2 + D b 3 y 3 = 10 ∙ 1/2 – 10 ∙ 0 + 20 ∙ 2 = = +45 ум. од. і становитиме max Z = 285 + 45 = 330 ум. од. 5. Оцінка рентабельності продукції, що виготовляється на підприємстві, виконується за допомогою двоїстих оцінок та обмежень двоїстої задачі, які характеризують кожний вид продукції. Підставимо Y * у систему обмежень двоїстої задачі. Якщо вартість ресурсів на одиницю продукції (ліва частина) перевищує ціну цієї продукції (права частина), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.
Аналогічні результати можна дістати, проаналізувавши двоїсті оцінки додаткових змінних, значення яких показують, на скільки вартість ресурсів перевищує ціну одиниці відповідної продукції. Тому, якщо додаткова змінна двоїстої задачі дорівнює нулю, то продукція рентабельна. І, навпаки, якщо уі ¹ 0, то відповідна продукція нерентабельна. Додаткові змінні двоїстої задачі розміщуються в оцінковому рядку останньої симплекс-таблиці у стовпчиках «х 1»—«х 4». Їх оптимальні значення у 4 = 5; у 5 = 5/2; у 6 = 0; у 7 = 0. Тому продукція А і В нерентабельна, а продукція С і Д — рентабельна. 6. Під впливом різних обставин ціна одиниці продукції на підприємстві може змінюватися (збільшуватися чи зменшуватися). І тому завжди цікаво знати, у межах яких змін ціни продукції кожного виду оптимальний план її виробництва залишається таким: Для визначення інтервалів зміни коефіцієнтів цільової функції скористаємось тим, що при цьому симплекс-таблиця, яка відповідає оптимальному плану, зберігає свій вигляд за винятком елементів оцінкового рядка. Нові оцінки (Zj – Cj) мають задовольняти умову оптимальності задачі максимізації, тобто бути невід’ємними. Зміну коефіцієнта С 1 позначимо D С 1. Оскільки х 1 — небазисна змінна, то в симплекс-таблиці зміниться лише відповідна оцінка Z 1 – C 1: (Z 1 – C 1) = 4 × (–2) + 0 × 1 +3 × 3/2 – (2 + D С 1) = 5 – D С 1. За умови Z 1 – C 1 ³ 0 дістанемо нерівність 5 – D С 1 ≥ 0, тобто D С 1 ≤ 5. Це означає, що коли ціна одиниці продукції А за інших однакових умов зросте не більш як на 5 ум. од., то оптимальним планом виробництва продукції на підприємстві все одно залишиться Х * = (0; 0; 35; 45). Лише максимальний дохід зміниться на max ∆ Z = D С 1 х 1. Аналогічно розраховується інтервал зміни коефіцієнта D С 2: (Z 2 – C 2) = 5/2 – D С 2 ≥ 0; D С 2 ≤ 5/2. Зі зростанням ціни одиниці продукції В на 5/2 ум. од. за інших однакових умов оптимальний план виробництва продукції не зміниться, а max ∆ Z = D С 2 Х 2. Дещо складніше розраховується інтервал зміни коефіцієнтів для базисних змінних. У цьому разі зміни відбуваються також у стовпчику «С баз» симплекс-таблиці, а це, у свою чергу, стосується всіх ненульових оцінок (Zj – Cj). Так, для базисної змінної х 3 зміна коефіцієнта на D С 3 приведе до таких оцінок: (Z 1 – C 1) = 4 × (–2) + 0 × (–1) +(3 + D С 3)× 5 – 2 = 5 + 5D С 3; (Z 2 – C 2) = 4 × 1/2 + 0 × 1 + (3 + D С 3)× 3/2 – 4 = 5/2 + 3/2D С 3; (Z 5 – C 5) = 4 × 1/2 + 0 × (–1) – 1/2 ∙ (3 + D С 3) – 0 = 1/2 – 1/2D С 3; (Z 7 – C 7) = 4 × (–1) + 0 × 0 + 2 ∙ (3 + D С 3) – 0 = 2 + 2D С 3. Нові значення оцінок мають задовольняти умову оптимальності, тобто Zj – Cj ≥ 0. Тому інтервал для D С 3 визначається з такої системи нерівностей:
Отже, ціна одиниці продукції С може збільшуватися та зменшуватися на 1 ум. од. і перебувати в межах від 2 до 4 ум. од., але оптимальним планом виробництва продукції залишається Для базисної невідомої х 4 інтервал зміни коефіцієнта С 4 розраховується аналогічно:
Якщо за інших однакових умов ціна одиниці продукції Д зменшиться до 3 ум. од. або збільшиться до 6 ум. од., то оптимальний план виробництва продукції на підприємстві не зміниться Якщо коливання ціни продукції виходять за визначені межі, то план Х * = (0; 0; 35; 45) вже не буде оптимальним і його необхідно буде поліпшити згідно з алгоритмом симплекс-методу, тобто продовжити розв’язування задачі. Виконаний у цій задачі аналіз лінійної моделі на чутливість дає широкий спектр динамічної інформації про визначений оптимальний план і дає змогу дослідити можливі зміни цього оптимального плану в результаті коректування умов прямої задачі.
Приклад 4.2. Фірма виготовляє продукцію трьох видів А, В і С. Для цього потрібний певний час обробки кожної продукції на різних групах обладнання (1, 2, 3) (див. таблицю).
Можливий час роботи обладнання кожного типу становить відповідно 360, 520 та 220 год на місяць. Ціна одиниці продукції А дорівнює 90 дол., продукції В — 110 дол., а продукції С — 150 дол. Визначити, яку продукцію і в якій кількості слід виготовляти, щоб фірма отримувала найбільший дохід. Розв’язування задачі симплекс-методом дає таку останню симплексну таблицю:
Керівництво фірми цікавить, чи зміниться оптимальний план виробництва продукції і якщо зміниться, то яким буде новий оптимальний план у кожній з наведених далі ситуацій. 1. Фірма може збільшити час роботи обладнання груп 2 та 3 відповідно на 100 та 80 год. за місяць, орендуючи для цього додаткове обладнання, яке коштуватиме 5000 дол. Чи вигідно це? Якщо вигідно, то яким має бути новий план виробництва продукції? 2. Фінансовий відділ фірми вважає, що загострення конкуренції на ринку збуту може призвести до зниження ціни на продукцію В на 25 дол. Як це позначиться на оптимальному плані виробництва продукції фірми? 3. Відділ досліджень і розробок фірми пропонує виготовляти дешевшу модифікацію продукції С. Для виробництва одиниці цієї нової продукції потрібний час роботи обладнання груп 1, 2 та 3 становить відповідно 4, 3 та 1 год. Орієнтовна ціна одиниці нової продукції дорівнює 120 дол. Керівництво фірми цікавить, чи буде за таких умов виробництво нової продукції вигідним. 4. Споживач продукції А за певних обставин порушує попередню домовленість і відмовляється прийняти більш як 100 од. продукції А. Визначити, як фірма має змінити план виробництва своєї продукції, щоб уникнути втрат, пов’язаних із надвиробництвом відповідного виду продукції. Розв’язування. Із наведеної в умові задачі симплекс-таблиці маємо: Х * = (180; 40; 0; 100; 0; 0), max Z = 20 600, Y * = (0; 10; 70). Оптимальним планом виробництва продукції на фірмі є випуск 180 од. продукції А та 40 од. продукції В. Виготовлення продукції виду С не передбачається. При цьому фірма отримає максимальний дохід у розмірі 20 600 дол. на місяць. 1. Збільшення часу роботи обладнання дасть змогу збільшити випуск продукції, тобто змінить оптимальний план і дохід фірми. Оскільки D b 1 = 0, D b 2 = 100, D b 3 = 80, новий оптимальний план визначається так:
Новий план допустимий (всі хj ≥ 0), і тому оптимальні двоїсті оцінки зберігають свої значення: Y * = (0; 10; 70). Приріст доходу фірми в результаті зміни оптимального плану виробництва продукції розраховується так: max ∆ Z = D b 1 y 1 + D b 2 y 2 + D b 3 y 3 = 100 ∙ 10 + 80 ∙ 70 = 6600 дол. Оскільки дохід фірми від додаткового використання обладнання груп 2 і 3 перевищує витрати на оренду цього обладнання (6600 > 5000), то природно, що така тактика фірми буде вигідною. При цьому оптимальним планом виробництва стане випуск 290 од. продукції А і 10 од. продукції В. Невикористаний час роботи обладнання групи 1 зменшиться до 50 год на місяць, а дохід фірми за відрахуванням витрат на оренду обладнання дорівнюватиме 20 600 + (6600 – 5000) = 22 200 дол. на місяць. 2. Зміна ціни одиниці продукції В на D С 2 (25 дол.) стосується всього оцінкового рядка симплекс-таблиці, оскільки х 2 є базисною змінною. Нові Zj – Cj матимуть такі значення: Z 3 – C 3 = 10 –D С 2 = 10 + 25 = 35; Z 5 – C 5 = 10 + 1/2D С 2 = 10 – 12,5 = –2,5; Z 6 – C 6 = 70 – D С 2 = 70 + 25 = 95. Коли б усі здобуті оцінки задовольняли умову Zj – Cj ≥ 0, то це означало б, що попри зниження ціни план виробництва продукції на фірмі не зміниться. Але оцінка Z 5 – C 5 не задовольняє умову оптимальності задачі на максимум, і тому можна зробити такий висновок. Істотне зниження ціни одиниці продукції В порушує визначений раніше оптимальний план виробництва продукції, оскільки випуск продукції виду В стає для фірми невигідним, нерентабельним. Новий оптимальний план визначається у процесі подальшого розв’язування задачі симплекс-методом:
Отже, у розглянутій ситуації зниження ціни одиниці продукції виду В на 25 дол. різко змінить структуру та обсяги виробництва продукції на фірмі. Вигідним стане випуск лише продукції А у кількості 220 од.: при цьому час роботи обладнання груп 1 і 2 використовуватиметься повністю. Усе це призведе до зменшення доходу фірми до 19 800 дол. на місяць. 3. Обсяг виробництва нової продукції в оптимальному плані позначимо х 7. Тоді математична модель прямої задачі матиме такий вигляд:
У математичній моделі двоїстої задачі змінній х 7 відповідатиме таке обмеження: Для цього за допомогою оберненої матриці необхідно визначити елементи стовпчика «х 7» останньої симплекс-таблиці:
Результати однієї ітерації симплекс-методу, що приводить до нового оптимального плану задачі, наведено далі.
Як бачимо з таблиці, Х * = (160; 20; 0; 0; 0; 0; 40), max Z = 21 400. Керівництво фірми має підтримати пропозицію відділу досліджень та розробок і налагодити виробництво нової продукції, яка є рентабельною, виготовляючи її в кількості 40 од.; відповідно продукції А — 160 од. і продукції В — 20 од. Такий новий оптимальний план виробництва продукції збільшить дохід фірми до 21 400 дол. на місяць. 4. Четверта запропонована ситуація математично пов’язана з уведенням в умову задачі додаткового обмеження, що може привести до таких наслідків: а) нове обмеження для визначеного оптимального плану виконується і тоді воно є надлишковим, зайвим і його включення до моделі не змінює визначеного плану; б) нове обмеження для визначеного оптимального плану не виконується, і тоді за допомогою двоїстого симплекс-методу необхідно знайти новий оптимальний план. За умовою задач додатковим є обмеження х 1 ≤ 100. Але воно суперечить оптимальній кількості продукції А, яка дорівнює 180 од. Тому необхідно приєднати це додаткове обмеження до симплекс-таблиці та продовжити розв’язування задачі, але вже за допомогою двоїстого симплекс-методу. Для цього спочатку зведемо додаткове обмеження до канонічного вигляду: х 1 + х 7 = 100. Оскільки в оптимальному плані змінна х 1 є базисною, її необхідно записати через небазисні невідомі. Це робиться так. У симплекс-таблиці, яку наведено в умові задачі, рядок змінної «х 1» подається рівнянням 1 · х 1 + 0 · х 2 + 3 · х 3 + 0 · х 4 – 1/2 · х 5 + 2 · х 6 = 180. З цього рівняння визначимо х 1: х 1 = 180 – 3 х 3 + 1/2 х 5 – 2 х 6. Підставивши цей вираз в додаткове обмеження, отримаємо 180 – 3 х 3 + 1/2 х 5 – 2 х 6 + х 7 = 100 або –3 х 3 + 1/2 х 5 – 2 х 6 + х 7 = –80. У такому вигляді додаткове обмеження дописується в симплекс-таблицю. Застосування двоїстого симплекс-методу приведе до нового оптимального плану задачі:
З останньої таблиці маємо Х * = (100; 200/3; 80/3; 20; 0;0), max Z = 61 000/3 ≈ 20 333. Проаналізуємо цей план. Реалізація запропонованої в умові задачі ситуації змінює структуру та кількісний вираз оптимального плану. Тепер з урахуванням вимог споживача фірма виготовлятиме 100 од. продукції А, 200/3 од. продукції В і 80/3 од. продукції С. У результаті такого плану випуску продукції дохід фірми зменшиться до 20 333 дол. на місяць.
4.2. Приклади та завдання для самостійної роботи У наведених далі задачах виконати такі дії: 1) записати математичні моделі прямої та двоїстої задач; 2) записати оптимальні плани прямої та двоїстої задач, подати їх економічний аналіз; 3) визначити статус ресурсів, що використовуються для виробництва продукції, та рентабельність кожного виду продукції; 4) обчислити інтервали стійкості двоїстих оцінок стосовно зміни запасів дефіцитних ресурсів; 5) розрахувати інтервали можливих змін ціни одиниці рентабельної продукції.
4.1 Підприємство виготовляє три види продукції А, В і С, використовуючи для цього три види ресурсів 1, 2, 3. Норми витрат усіх ресурсів на одиницю продукції та запаси ресурсів наведено в таблиці:
Відома ціна одиниці продукції кожного виду: А — 9 ум. од., В — 10 ум. од. і С — 16 ум. од. Визначити план виробництва продукції, що забезпечує підприємству найбільший дохід. Остання симплекс-таблиці даної задачі має такий вигляд:
4.2 Підприємство виготовляє продукцію А, В і С, для чого використовує три види ресурсів 1, 2, 3. Норма витрат усіх ресурсів на одиницю кожної продукції та обсяги ресурсів на підприємстві наведено в таблиці:
Відома ціна одиниці продукції кожного виду: А — 10 ум. од., В — 14 ум. од. і С — 12 ум. од. Визначити план виробництва продукції, що забезпечує підприємству найбільший дохід. Остання симплекс-таблиця, що містить оптимальний план задачі, має такий вигляд:
4.3 Підприємство виготовляє продукцію чотирьох видів А, В, С і Д, для чого використовує три види ресурсів 1, 2, 3. Норми витрат ресурсів на одиницю продукції та запаси ресурсів на підприємстві наведено в таблиці:
Відома ціна одиниці продукції кожного виду продукції: А — 4 ум. од., В — 3 ум. од., С — 6 ум. од., Д — 7 ум. од. Визначити план виробництва продукції, який максимізує дохід підприємства. Остання симплекс-таблиця має такий вигляд:
4.4 Підприємство виготовляє продукцію чотирьох видів з трьох видів ресурсів. Економічні показники виробництва наведено в таблиці. Визначити такий план виробництва продукції всіх видів, який забезпечить підприємству найбільший дохід.
Симплекс-таблиця, що відповідає оптимальному плану задачі, має такий вигляд:
4.5 Підприємство виготовляє продукцію чотирьох видів А, В, С і Д. Для цього використовуються ресурси трьох видів 1, 2, 3. Основні економічні показники процесу виробництва продукції на підприємстві наведено в таблиці:
Визначити план виробництва продукції, який заб
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.17.60 (0.013 с.) |


 ;
;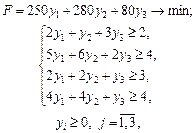
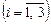 .
. = (1/2; 0; 2);
= (1/2; 0; 2);
 збільшиться на 1/2, змінної
збільшиться на 1/2, змінної  — зменшиться на одиницю, а
— зменшиться на одиницю, а  — на 1/2. При цьому структура плану не зміниться, а нові оптимальні значення змінних будуть такими:
— на 1/2. При цьому структура плану не зміниться, а нові оптимальні значення змінних будуть такими: , то новий оптимальний план
, то новий оптимальний план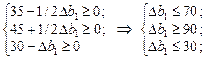
 .
. ,
,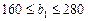 .
. ,
, ,
,
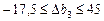 ,
, .
. ;
; .
. .
. .
. ,
,

 ,
, .
.
 ,
, .
.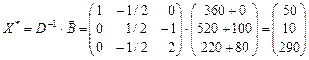 .
.
 ← х 2
← х 2

 х 1
х 1

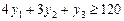 . Оцінимо рентабельність нової продукції за допомогою двоїстих оцінок: 4 · 0 + 3 · 10 + 1 ∙ 70 = 100, що є меншим за 120 дол. Загальна вартість усіх ресурсів, що витрачаються на випуск одиниці нової продукції, не перевищує орієнтовної ціни цієї продукції, і тому її виробництво для фірми є вигідним, рентабельним. Завдяки цьому визначений раніше оптимальний план виробництва продукції можна поліпшити за рахунок уведення в нього х 7.
. Оцінимо рентабельність нової продукції за допомогою двоїстих оцінок: 4 · 0 + 3 · 10 + 1 ∙ 70 = 100, що є меншим за 120 дол. Загальна вартість усіх ресурсів, що витрачаються на випуск одиниці нової продукції, не перевищує орієнтовної ціни цієї продукції, і тому її виробництво для фірми є вигідним, рентабельним. Завдяки цьому визначений раніше оптимальний план виробництва продукції можна поліпшити за рахунок уведення в нього х 7.
 ← х 7
← х 7
 Zj – Cj ≥ 0
Zj – Cj ≥ 0



