
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рекомендації щодо розв’язування задачСодержание книги
Поиск на нашем сайте
Передмова Методичні вказівки з обраної теми складені відповідно до діючої програми курсу загальної фізики для вищих навчальних закладів. Вони містять приклади рішення типових задач, а також приклади завдань для самостійного розв’язування. Рівень складності задач досить різноманітний. Разом з типовими задачами наведені приклади розв’язування і досить складних задач з курсу загальної фізики. На початку посібника наведені теоретичні відомості, на яких базуються запропоновані задачі. Тому вказівки можуть використовуватися викладачами як методичний матеріал при проведенні практичних занять. При написанні методичних вказівок поряд з оригінальними задачами вміщено задачі з інших збірників, які, на погляд автора, мають науково–методичну цінність. Мета роботи Основна мета представленої роботи – допомогти курсантам у вивченні курсу загальної фізики. Робота складається з трьох частин. У теоретичній частині відповідно до сучасних вимог наведені основні поняття, закони і формули обраної теми. Доцільність досить детального теоретичного огляду у роботі, яка має практичну спрямованість обумовлена тим, що теоретичний матеріал в існуючих курсах загальної фізики досить великий, і студенти не завжди можуть виділити головне, необхідне для розв’язання задач з обраної теми. У другому розділі наведені приклади розв’язування задач, які добрані так, щоб якомога повніше охопити фізичні ситуації, характерні для теми. Приклади розв’язків систематизовані. Тому під час роботи з посібником їх варто розглядати у тому порядку, в якому вони наведені: часто наступні прилади ґрунтуються на попередніх. Структура заняття При проведенні практичного заняття з курсу загальної фізики слід дотримуватися наступної послідовності: на початку заняття курсантам наводять теоретичні відомості, на яких базуються розв’язки запропонованих в подальшому задач. На другому етапі показують приклада розв’язування задач з обраної теми. На фізичному етапі розв’язування задачі слід звертати увагу на процес побудови моделі і на її схематичне зображення. Тут важливим є обґрунтування правомірності застосування певного загального закону або формули для конкретного явища, яке розглядається в задачі. Скорочений запис проводиться у систематизованій формі відповідно до позначень схематичного зображення моделі. Фізичний етап розв’язання задачі завершується складанням системи рівнянь, кількість яких не менша кількості невідомих. На математичному етапі розв’язується отримана система рівнянь відносно невідомої величини. Третій етап – інтерпретаційний, на якому аналізується отриманий результат на відповідність запропонованої моделі.
На третьому етапі курсантам пропонуються задачі для самостійного розв’язування. За умови вдумливого та наполегливого опрацювання теоретичного матеріалу та прикладів розв’язків, курсанти з запропонованими задачами можуть впоратись самостійно. Це сприятиме розвитку в них творчих здібностей, вмінь та навичок. Задачі, які курсанти не встигли розв’язати на занятті, залишаються для домашнього опрацьовування.
Вимоги до оформлення задач Розв’язування задач повинно супроводжуватися поясненнями. У поясненнях необхідно вказувати ті основні закони і формули, на яких базується розв’язок даної задачі. Розв’язок задачі рекомендується спочатку зробити в загальному вигляді, тобто тільки в літерних позначеннях, пояснюючи застосовувані при написанні формул літерні позначення. Обчислення варто проводити шляхом підстановки заданих числових величин у розрахункову формулу. Перевірити одиниці вимірювання отриманих величин по розрахунковій формулі і тим самим підтвердити її правильність. Точність розрахунку визначається числом значущих цифр вихідних даних. Константи фізичних величин і інших довідкових даних вибираються з таблиць. Отриманий результат наприкінці розв’язування необхідно перевірити на адекватність реальним умовам, що представлені в запропонованій задачі. Рекомендації щодо розв’язування задач При вивченні теми «механічні коливання» основну увагу слід приділити основному рівнянню гармонічних коливань. При визначенні періоду коливань розглядають мале відхилення від положення рівноваги і відшукують силу (або момент сили), що прагне повернути тіло в положення рівноваги. Ця сила (або момент) буде прямо пропорціональною відхиленню. Отримав основне рівняння гармонічних коливань, знаходимо циклічну частоту і період.
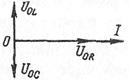
Усі типові задачі на електромагнітні коливання можна розв'язати аналітичним методом, користуючись основними формулами. Але розв'язування задач, особливо на змінні струми, дуже полегшується, якщо застосувати графічний метод, тобто метод векторних діаграм напруг і струмів. Векторну діаграму напруг для кола змінного струму з послідовно ввімкненими індуктивністю і ємністю будують так. У певному масштабі вздовж довільної осі X відкладають вектор спаду напруги на активному опорі Ua. Напруга на індуктивному опорі випереджає за фазою струм на p/2, тому відкладають UL перпендикулярно до Ua в бік збільшення кутів. Вектор спаду напруги Uc на ємнісному опорі відстає від струму на p/2. Отже, вектори UL і Uc спрямовані в протилежні сторони. Результуючу напругу U визначають простим геометричним додаванням. З трикутника напруг легко визначити кут j – зсув фаз між струмом і напругою. Для графічного визначення повного опору змінного струму, якщо відомі активний, індуктивний і ємнісний опори, можна побудувати прямокутний трикутник опорів. Катети цього трикутника дорівнюватимуть активному і реактивному опорам,, а гіпотенуза дорівнюватиме повному опору. Порядок зарахування Перевірка знань курсантів відбувається під час контрольних заходів в сугубо письмовій формі. Курсантам пропонується п’ять задач з тем, які були опрацьовані за минулий період. Отримана оцінка залежить від якості розв’язування і оформлення запропонованих задач. Практичне заняття № 15 Тема: Механічні коливання і хвилі Теоретичні відомості Коливальним називають рух, у якому матеріальна точка або система точок, багаторазово відхиляючись від свого положення рівноваги, щоразу знову повертається до нього. Коливання називають вільними, якщо вони відбуваються в замкненій системі за рахунок енергії, що передана системі в початковий момент часу. Якщо коливання відбуваються під дією зовнішніх сил, то їх називають вимушеними. Коливання, при яких значення величин, що змінюються, повторюється через однаковий проміжок часу, називають періодичними. Основні характеристики періодичних коливань: - період (Т) – час одного повного коливання:
де N – кількість коливань за час t. [Т] = [c]; - частота (n) – число коливань за одиницю часу:
- амплітуда (А) – максимальне значення змінюваної величини; - фаза (j) – величина, яка визначає значення змінюваної величини в заданий момент часу; - початкова фаза (j0) – визначає значення змінюваної величини у початковий момент часу; - циклічна частота (w) – фізична величина, яка показує, як швидко змінюється фаза за одиницю часу:
Гармонічними називають коливання, в яких величина, яка нас цікавить, змінюється у часі за законом синуса або косинуса:
де w0 – власна циклічна частота коливань, Так як при гармонічних коливаннях за період фаза змінюється на 2p, то формула знаходження циклічної частоти приймає вигляд:
Знайдемо залежність швидкості і прискорення від часу. Для цього здиференціюємо рівняння (1) за часом:
Зіставивши (3) і (1), отримуємо:
Це диференціальне рівняння називають рівнянням гармонічного осцилятора або рівнянням вільних незатухаючих гармонічних коливань.. Його розв’язок
та
Звідси знаходимо шукані сталі:
Питання для перевірки знань 1. Механічні коливання і їхні характеристики. Кінематика гармонічних коливань. 2. Динаміка гармонічних коливань. Пружний, математичний та фізичний маятники. 3. Енергія коливального руху. 4. Затухаючи коливання. Характеристики затухання. 5. Вимушені коливання. Явище резонансу.
Практичне заняття № 16 Тема: Електромагнітні коливання і хвилі Теоретичні відомості Електричними називають коливання, при яких електричні величини (заряди, струми, напруга, тощо) періодично змінюються і які супроводжуються взаємними перетвореннями електричного і магнітного полів. Якщо миттєве значення струму однаково на всіх ділянках електричного кола, то струм називають квазістаціонарним. Нехай
Коливальним контуром називається електричне коло, складене з конденсатора і котушки індуктивності. У такому контурі можуть виникати електричні коливання. Нехай активний опір кола дуже малий. Якщо зарядити конденсатор до напруги
де
Якщо замкнути електричне коло, то конденсатор почне розряджатись через котушку індуктивності. Цей розряд не буде миттєвий, бо з виникненням струму в котушці збуджуватиметься ЕРС самоіндукції, яка, за законом Ленца, протидіятиме наростанню струму. Через час
У наступний момент часу струм у котушці спадатиме до нуля, але поступово, оскільки його підтримуватиме ЕРС самоіндукції. Завдяки цьому струму конденсатор перезарядиться. У момент часу
Електромагнітні коливання можна порівняти з коливаннями маятника. При цьому електричній енергії відповідає потенціальна енергія маятника, а магнітній енергії – кінетична. Коливання, які відбуваються під дією процесів у самому коливальному контурі без зовнішніх впливів і втрат енергії на тепло та електромагнітне випромінювання, називаються власними електромагнітними коливаннями. Нехай у момент часу і напруга на обкладках конденсатора
Тоді миттєва сила розрядного струму за законом Ома
або
Оскільки
Отримане лінійне диференційне рівняння другого порядку називають рівнянням коливального контуру. Для власних коливань R = 0, тоді
Як відомо, розв'язком отриманого рівняння є гармонічна функція
де Остання формула називається формулою Томсона. Відповідно до зміни величини заряду на обкладках конденсатора змінюється напруга на конденсаторі і сила розрядного струму в контурі:
У реальному контурі
Перепишемо отримане рівняння у вигляді:
де Розв’язком цього рівняння за умовою
де Затухання коливань оцінюють декрементом затухання, що дорівнює відношенню двох послідовних амплітуд через проміжок часу один період, тобто
Логарифмічний декремент затухання дорівнює
Добротність коливального контуру визначається за формулою:
При малому затуханні
де За законом електромагнітної індукції
Якщо рамка складається не з одного, а з n витків, то ЕРС індукції
де Під’єднавши до рамки навантаження, отримуємо струм, який змінюється за модулем та напрямком, тобто змінний струм. Амперметр і вольтметр у колі змінного струму показують не миттєві й не максимальні значення струму і напруги, а ефективні або діючі. Поняття діючого значення сили струму водять так: пропускають через опір R спочатку постійний, а потім змінний струм і регулюючи силу струму досягають, щоб за однаковий час в обох випадках на опорі виділилося однакова кількість тепла. Діюче, або ефективне, значення сили змінного струму дорівнює силі такого постійного струму, який за той самий проміжок часу виділяє в деякому опорі таку саму кількість тепла, як і даний змінний струм. Знайдемо співвідношення між ефективними і амплітудними значеннями сили і напруги змінного струму. Для цього обчислимо кількість теплоти, яку виділяють названі струми за час Т, що дорівнює періоду змінного струму. Кількість теплоти, яка виділяється при проходженні постійного струму:
Кількість теплоти, яка виділяється при проходженні змінного струму:
Відповідно до останньої рівності
Розглянемо загальний випадок кола змінного струму з послідовно увімкненими резистором, котушкою індуктивності і конденсатором. Вважатимемо, що на цих складових кола зосереджені відповідно весь активний опір R, вся індуктивність L і ємність С. До розглядуваного кола застосуємо другий закон Кірхгофа. Враховуючи спади напруги на резисторі і конденсаторі та збудження ЕРС самоіндукції на котушці індуктивності, запишемо:
Враховуючи, що
Розв’язок отриманого рівняння має вигляд:
Враховуючи, що
де Для знаходження
Із отриманих рівнянь свідчить, що на активному опорі сила струму за фазою збігається з напругою, на індуктивності сила струму відстає за фазою на
Рівняння (6) або Розглянемо випадок, коли індуктивний опір кола дорівнює ємнісному опору:
Тоді
або
тобто спад напруги на кінцях котушки індуктивності дорівнює спаду напруги на обкладках конденсатора. Ці напруги перебувають у протифазах і взаємно зрівноважуються. Такі умови називаються резонансом напруг. Характерні особливості резонансу напруг такі: - повний опір кола мінімальний і дорівнює активному опору; - амплітуда струму має найбільше значення; - амплітуда напруги на активному опорі дорівнює амплітуді прикладеної напруги; - напруга і струм перебувають в однакових фазах; -
Щоб знайти сили струму в головному провіднику, побудуємо векторну діаграму сил струмів, узявши за опорну лінію вектор напруги. Але до цього способом введення в у котушку залізного осердя підберемо такі умови, щоб індуктивний опір дорівнював ємнісному:
Тоді струми в обох вітках будуть однакові, протифазні і взаємно зрівноважені. Отже, струм у головному провіднику дорівнюватиме нулю, а опір кола буде нескінченно великий. Насправді позбавитися від активного опору неможливо і струм у головному провіднику буде мінімальний, а опір кола максимальний. Такі умови називаються резонансом струмів. Хоч загальний струм і малий, але струми через конденсатор і котушку можуть бути досить великими. Питання для перевірки знань 1. Електричні коливання. Коливальний контур. Рівняння коливального контуру. Формула Томсона. 2. Затухаючи електромагнітні коливання і їхні характеристики. 3. Змінний електричний струм. Діючи значення сили струму і напруги. 4. Послідовне коло змінного струму. Закон Ома. Активний, реактивний та повний опір кола змінного струму. 5. Резонанс струмів і напруг. Умови резонансу. 6. Потужність у колі змінного струму.
Список рекомендованої літератури 1. Волькенштейн В.С. Сборник задач по общему курсу физики. – М.:Наука, 1985. – 384с. 2. А.Г.Чертов, А.А. Воробьев, Задачник по физике.– М.: Высшая школа. – 1981. – 490 с. 3. Савельев И.В. Курс общей физики. т. 2. Электричество и магнетизм. Волны. Оптика: Учебное пособие. – М.: Наука, 1989. – 352 с. 4. Трофимова Т.И. Курс физики: Уч. Пособие для вузов.–М.: Вісш. шк., 2000.–542с. Передмова Методичні вказівки з обраної теми складені відповідно до діючої програми курсу загальної фізики для вищих навчальних закладів. Вони містять приклади рішення типових задач, а також приклади завдань для самостійного розв’язування. Рівень складності задач досить різноманітний. Разом з типовими задачами наведені приклади розв’язування і досить складних задач з курсу загальної фізики. На початку посібника наведені теоретичні відомості, на яких базуються запропоновані задачі. Тому вказівки можуть використовуватися викладачами як методичний матеріал при проведенні практичних занять. При написанні методичних вказівок поряд з оригінальними задачами вміщено задачі з інших збірників, які, на погляд автора, мають науково–методичну цінність. Мета роботи Основна мета представленої роботи – допомогти курсантам у вивченні курсу загальної фізики. Робота складається з трьох частин. У теоретичній частині відповідно до сучасних вимог наведені основні поняття, закони і формули обраної теми. Доцільність досить детального теоретичного огляду у роботі, яка має практичну спрямованість обумовлена тим, що теоретичний матеріал в існуючих курсах загальної фізики досить великий, і студенти не завжди можуть виділити головне, необхідне для розв’язання задач з обраної теми. У другому розділі наведені приклади розв’язування задач, які добрані так, щоб якомога повніше охопити фізичні ситуації, характерні для теми. Приклади розв’язків систематизовані. Тому під час роботи з посібником їх варто розглядати у тому порядку, в якому вони наведені: часто наступні прилади ґрунтуються на попередніх. Структура заняття При проведенні практичного заняття з курсу загальної фізики слід дотримуватися наступної послідовності: на початку заняття курсантам наводять теоретичні відомості, на яких базуються розв’язки запропонованих в подальшому задач. На другому етапі показують приклада розв’язування задач з обраної теми. На фізичному етапі розв’язування задачі слід звертати увагу на процес побудови моделі і на її схематичне зображення. Тут важливим є обґрунтування правомірності застосування певного загального закону або формули для конкретного явища, яке розглядається в задачі. Скорочений запис проводиться у систематизованій формі відповідно до позначень схематичного зображення моделі. Фізичний етап розв’язання задачі завершується складанням системи рівнянь, кількість яких не менша кількості невідомих. На математичному етапі розв’язується отримана система рівнянь відносно невідомої величини. Третій етап – інтерпретаційний, на якому аналізується отриманий результат на відповідність запропонованої моделі. На третьому етапі курсантам пропонуються задачі для самостійного розв’язування. За умови вдумливого та наполегливого опрацювання теоретичного матеріалу та прикладів розв’язків, курсанти з запропонованими задачами можуть впоратись самостійно. Це сприятиме розвитку в них творчих здібностей, вмінь та навичок. Задачі, які курсанти не встигли розв’язати на занятті, залишаються для домашнього опрацьовування.
Вимоги до оформлення задач Розв’язування задач повинно супроводжуватися поясненнями. У поясненнях необхідно вказувати ті основні закони і формули, на яких базується розв’язок даної задачі. Розв’язок задачі рекомендується спочатку зробити в загальному вигляді, тобто тільки в літерних позначеннях, пояснюючи застосовувані при написанні формул літерні позначення. Обчислення варто проводити шляхом підстановки заданих числових величин у розрахункову формулу. Перевірити одиниці вимірювання отриманих величин по розрахунковій формулі і тим самим підтвердити її правильність. Точність розрахунку визначається числом значущих цифр вихідних даних. Константи фізичних величин і інших довідкових даних вибираються з таблиць. Отриманий результат наприкінці розв’язування необхідно перевірити на адекватність реальним умовам, що представлені в запропонованій задачі. Рекомендації щодо розв’язування задач При вивченні теми «механічні коливання» основну увагу слід приділити основному рівнянню гармонічних коливань. При визначенні періоду коливань розглядають мале відхилення від положення рівноваги і відшукують силу (або момент сили), що прагне повернути тіло в положення рівноваги. Ця сила (або момент) буде прямо пропорціональною відхиленню. Отримав основне рівняння гармонічних коливань, знаходимо циклічну частоту і період. Усі типові задачі на електромагнітні коливання можна розв'язати аналітичним методом, користуючись основними формулами. Але розв'язування задач, особливо на змінні струми, дуже полегшується, якщо застосувати графічний метод, тобто метод векторних діаграм напруг і струмів. Векторну діаграму напруг для кола змінного струму з послідовно ввімкненими індуктивністю і ємністю будують так. У певному масштабі вздовж довільної осі X відкладають вектор спаду напруги на активному опорі Ua. Напруга на індуктивному опорі випереджає за фазою струм на p/2, тому відкладають UL перпендикулярно до Ua в бік збільшення кутів. Вектор спаду напруги Uc на ємнісному опорі відстає від струму на p/2. Отже, вектори UL і Uc спрямовані в протилежні сторони. Результуючу напругу U визначають простим геометричним додаванням. З трикутника напруг легко визначити кут j – зсув фаз між струмом і напругою. Для графічного визначення повного опору змінного струму, якщо відомі активний, індуктивний і ємнісний опори, можна побудувати прямокутний трикутник опорів. Катети цього трикутника дорівнюватимуть активному і реактивному опорам,, а гіпотенуза дорівнюватиме повному опору. Порядок зарахування Перевірка знань курсантів відбувається під час контрольних заходів в сугубо письмовій формі. Курсантам пропонується п’ять задач з тем, які були опрацьовані за минулий період. Отримана оцінка залежить від якості розв’язування і оформлення запропонованих задач. Практичне заняття № 15 Тема: Механічні коливання і хвилі Теоретичні відомості Коливальним називають рух, у якому матеріальна точка або система точок, багаторазово відхиляючись від свого положення рівноваги, щоразу знову повертається до нього. Коливання називають вільними, якщо вони відбуваються в замкненій системі за рахунок енергії, що передана системі в початковий момент часу. Якщо коливання відбуваються під дією зовнішніх сил, то їх називають вимушеними. Коливання, при яких значення величин, що змінюються, повторюється через однаковий проміжок часу, називають періодичними. Основні характеристики періодичних коливань: - період (Т) – час одного повного коливання:
де N – кількість коливань за час t. [Т] = [c]; - частота (n) – число коливань за одиницю часу:
- амплітуда (А) – максимальне значення змінюваної величини; - фаза (j) – величина, яка визначає значення змінюваної величини в заданий момент часу; - початкова фаза (j0) – визначає значення змінюваної величини у початковий момент часу; - циклічна частота (w) – фізична величина, яка показує, як швидко змінюється фаза за одиницю часу:
Гармонічними називають коливання, в яких величина, яка нас цікавить, змінюється у часі за законом синуса або косинуса:
де w0 – власна циклічна частота коливань, Так як при гармонічних коливаннях за період фаза змінюється на 2p, то формула знаходження циклічної частоти приймає вигляд:
Знайдемо залежність швидкості і прискорення від часу. Для цього здиференціюємо рівняння (1) за часом:
Зіставивши (3) і (1), отримуємо:
Це диференціальне рівняння називають рівнянням гармонічного осцилятора або рівнянням вільних незатухаючих гармонічних коливань.. Його розв’язок
та
Звідси знаходимо шукані сталі:
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.116.96 (0.018 с.) |

 ,
, або
або  . [n]=[c–1]=[Гц];
. [n]=[c–1]=[Гц];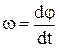 , [w] = [рад/с].
, [w] = [рад/с]. , (1)
, (1) – фаза коливань.
– фаза коливань. .
. (2)
(2) (3)
(3) З отриманих виразів видно, що швидкість
З отриманих виразів видно, що швидкість 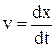 і прискорення
і прискорення  також змінюються по гармонічному закону з амплітудами
також змінюються по гармонічному закону з амплітудами  і
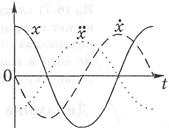
і  відповідно. При цьому швидкість випереджає миттєве значення х по фазі на p/2, а прискорення – на p, тобто миттєве значення прискорення знаходиться в противофазі з х. Графіки залежностей x(t),
відповідно. При цьому швидкість випереджає миттєве значення х по фазі на p/2, а прискорення – на p, тобто миттєве значення прискорення знаходиться в противофазі з х. Графіки залежностей x(t), 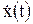 і
і  для випадку j0=0 показані на малюнку.
для випадку j0=0 показані на малюнку. (4)
(4) у початковий момент t = 0:
у початковий момент t = 0:
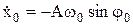 .
.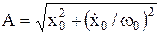 ,
,  .
. – довжина електричного кола, с – швидкість передачі електромагнітного збурення. Тоді час, за який передається це збурення, можно знайти як
– довжина електричного кола, с – швидкість передачі електромагнітного збурення. Тоді час, за який передається це збурення, можно знайти як 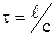 . Для періодично змінюваних струмів умова квазістаціонарності буде мати вигляд:
. Для періодично змінюваних струмів умова квазістаціонарності буде мати вигляд: .
. ,
, – заряд конденсатора, то цим самим між його обкладками буде наведене електричне поле з енергією
– заряд конденсатора, то цим самим між його обкладками буде наведене електричне поле з енергією .
. конденсатор повністю розрядиться і розрядний струм досягне найбільшого значення
конденсатор повністю розрядиться і розрядний струм досягне найбільшого значення  . В котушці індуктивності буде наведене магнітне поле. При цьому, очевидно, енергія електричного поля повністю перетвориться в енергію магнітного поля
. В котушці індуктивності буде наведене магнітне поле. При цьому, очевидно, енергія електричного поля повністю перетвориться в енергію магнітного поля .
. між обкладками конденсатора знову існуватиме електричне поле, але протилежного напряму. Наступне розряджання конденсатора проходитиме аналогічно початковому. Так у контурі відбувається періодичний рух електронів від однієї обкладки конденсатора до іншої, і, навпаки, з частотою, яка залежить від параметрів контура L, С, R. Одночасно з рухами електронів у контурі періодично змінюються всі електричні й магнітні величини, тобто відбуваються електромагнітні коливання.
між обкладками конденсатора знову існуватиме електричне поле, але протилежного напряму. Наступне розряджання конденсатора проходитиме аналогічно початковому. Так у контурі відбувається періодичний рух електронів від однієї обкладки конденсатора до іншої, і, навпаки, з частотою, яка залежить від параметрів контура L, С, R. Одночасно з рухами електронів у контурі періодично змінюються всі електричні й магнітні величини, тобто відбуваються електромагнітні коливання.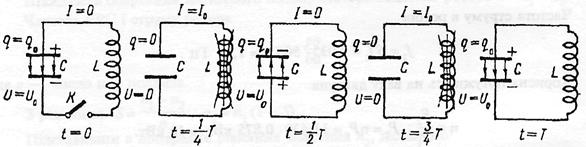
 , і ЕРС самоіндукції
, і ЕРС самоіндукції .
.
 . (*)
. (*) і
і  , то формулу (*) запишемо так:
, то формулу (*) запишемо так: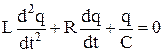 .
. .
.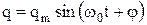 ,
, – власна циклічна частота контура і
– власна циклічна частота контура і  – період власних коливань в контурі.
– період власних коливань в контурі. ;
; .
.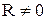 і частина енергії розрядного струму витрачається на нагрівання провідників, тому електричні коливання затухають. Електричні коливання в реальному контурі описуються диференціальним рівнянням:
і частина енергії розрядного струму витрачається на нагрівання провідників, тому електричні коливання затухають. Електричні коливання в реальному контурі описуються диференціальним рівнянням: ,
, – коефіцієнт затухання.
– коефіцієнт затухання. ;
;  ;
; 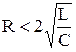 є функція
є функція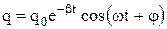 ,
, – циклічна частота власних коливань.
– циклічна частота власних коливань.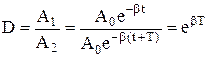 .
. .
. .
. .
. Змінним електричним струмом називають такий струм, сила і напруга якого змінюються за величиною і напрямом. Нехай рамка з провідника рівномірно обертається в однорідному магнітному полі відносно осі, перпендикулярної до напряму ліній магнітної індукції. Магнітний потік, який пронизує контур рамки, виражається так:
Змінним електричним струмом називають такий струм, сила і напруга якого змінюються за величиною і напрямом. Нехай рамка з провідника рівномірно обертається в однорідному магнітному полі відносно осі, перпендикулярної до напряму ліній магнітної індукції. Магнітний потік, який пронизує контур рамки, виражається так: ,
, – фаза, або кут між напрямом нормалі
– фаза, або кут між напрямом нормалі  до площини рамки і напрямом вектора
до площини рамки і напрямом вектора 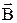 ; w – циклічна частота; S – площа рамки; Фо – максимальне значення магнітного потоку.
; w – циклічна частота; S – площа рамки; Фо – максимальне значення магнітного потоку. .
. ,
, – амплітудне значення ЕРС.
– амплітудне значення ЕРС. . (1)
. (1) , (2)
, (2)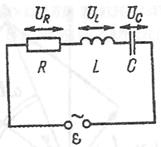 де інтеграл від другого члена суми дорівнює нулю. З рівності значень (1) і (2) дістаємо
де інтеграл від другого члена суми дорівнює нулю. З рівності значень (1) і (2) дістаємо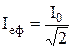 .
. .
.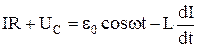 (3)
(3) , а
, а  , перепишемо рівняння (1) у вигляді:
, перепишемо рівняння (1) у вигляді: (4)
(4) , де
, де 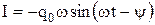 .
. , отримуємо:
, отримуємо: ,
,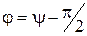 – зсув фаз між струмом і зовнішньою ЕРС, а
– зсув фаз між струмом і зовнішньою ЕРС, а  – амплітуда сили струму у колі.
– амплітуда сили струму у колі. і j представимо рівняння (4) у вигляді:
і j представимо рівняння (4) у вигляді: , (5)
, (5) де
де  – напруга на активному опорі,
– напруга на активному опорі,  – напруга на конденсаторі,
– напруга на конденсаторі,  – напруга на індуктивності.
– напруга на індуктивності. від напруги, на конденсаторі сила струму за фазою випереджає напругу на
від напруги, на конденсаторі сила струму за фазою випереджає напругу на  , (6)
, (6) , (7)
, (7) . (8)
. (8)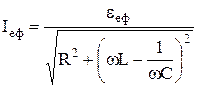 виражає закон Ома для змінного струму, в якому всі елементи з’єднані послідовно,
виражає закон Ома для змінного струму, в якому всі елементи з’єднані послідовно,  – індуктивний опір,
– індуктивний опір, 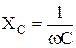 – ємнісний опір,
– ємнісний опір,  – повний опір кола змінного струму.
– повний опір кола змінного струму. .
.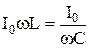 ,
,

 потужність джерела струму передається тільки активному опору, корисна потужність змінного струму максимальна.
потужність джерела струму передається тільки активному опору, корисна потужність змінного струму максимальна.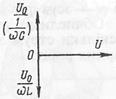 Розглянемо випадок паралельного вмикання котушки індуктивності і конденсатора в коло змінного струму за умови, що активний опір ділянок малий і ним можна знехтувати. Напруга на клемах
Розглянемо випадок паралельного вмикання котушки індуктивності і конденсатора в коло змінного струму за умови, що активний опір ділянок малий і ним можна знехтувати. Напруга на клемах  . Оскільки напруга на обох ділянках паралельного з'єднання однакова, то зсув фаз позначатиметься тільки на формулах сили струму на різних ділянках, а саме:
. Оскільки напруга на обох ділянках паралельного з'єднання однакова, то зсув фаз позначатиметься тільки на формулах сили струму на різних ділянках, а саме: і
і  .
.


