
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динаміка гармонічних коливань.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пружній маятник. Нехай кулька маси m підвішена на невагомій пружині жорсткості k, здійснює вертикальні коливання. У положенні рівноваги, в точці О, сила тяжіння зрівноважується силою пружності:
Якщо кульку вивести з положення рівноваги і вважати додатним напрямом зміщення х від положення рівноваги вниз, то рівняння динаміки для кульки матиме такий вигляд:
а враховуючи (5) отримуємо:
або, після перетворення
Легко перевірити підстановкою, що розв'язок цього рівняння виражає гармонічне коливання
з циклічною частотою
і періодом
Математичний маятник. Математичним маятником називають матеріальну точку, підвішену на невагомій і нерозтяжній нитці, що коливається у вертикальній площині під дією сили тяжіння. Нехай маса маятника m, а довжина нитки підвішування l. З відхиленням маятника від положення рівноваги виникає повертаюча сила
де Складова
де х – зміщення маятника від положення рівноваги, а знак мінус показує, що повертаюча сила протилежна до напряму зміщення. Враховуючи, що за другим законом Ньютона
звідки
Період коливання математичного маятника:
З формули періоду коливання випливають такі закономірності коливання математичного маятника: - період коливання маятника не залежить від його маси; - період коливання не залежить від амплітуди; - період коливання прямо пропорційний квадратному кореню з довжини маятника і обернено пропорційний квадратному кореню з прискорення вільного падіння.
де L – відстань центра маси від точки підвішування. При малих кутах відхилення
Після відповідних підстановок матимемо рівняння фізичного маятника:
де I – момент інерції тіла відносно осі коливання. Це рівняння цілком аналогічне рівнянню динаміки гармонічного осцилятора. І в цьому разі легко перевірити підстановкою, що розв'язок отриманого рівняння задає гармонічне коливання:
з циклічною частотою
і періодом коливання
Фізичний маятник можна розглядати і як сукупність багатьох математичних маятників різної довжини. Оскільки вони жорстко зв'язані, то короткі маятники спонукають фізичний маятник до частіших коливань, а довгі – до повільніших. Для кожного фізичного маятника можна підібрати такий математичний маятник, який матиме однаковий період коливання з даним фізичним. Довжина такого математичного маятника, який має однаковий період з даним фізичним, називається зведеною довжиною фізичного маятника. З рівності періодів коливання цих маятників можна знайти вираз для зведеної довжини l0 фізичного маятника:
Точка на фізичному маятнику О1 що відповідає зведеній довжині, називається центром коливань. Центр коливань і точка підвішування – спряжеш точки. Якщо їх поміняти ролями, то період фізичного маятника не зміниться. Енергія коливального руху. Щоб надати матеріальній точці коливального руху, треба вивести її з положення рівноваги. Для цього виконують певну роботу проти повертаючої сили. Ця робота буде мірою потенціальної енергії, наданої точці ззовні:
Із отриманого рівняння випливає, що потенціальна енергія точки в коливальному русі пропорційна квадрату її зміщення з положення рівноваги. Після припинення дії зовнішньої сили точка повертатиметься до положення рівноваги під дією квазіпружної сили. У міру зменшення зміщення, відповідно до закону збереження енергії, потенціальна енергія точки перетворюватиметься в кінетичну енергію. Оскільки зміщення точки
Кінетичну енергію точки з масою m і швидкістю v запишемо так:
У положеннях крайнього зміщення потенціальна енергія максимальна, а кінетична дорівнює нулю. З рухом до положення рівноваги потенціальна енергія зменшується, а кінетична збільшується; у момент рівноваги потенціальна енергія дорівнює нулю, а кінетична набуває максимального значення. Повна енергія точки в коливальному русі складається із суми потенціальної і кінетичної енергії:
або після спрощення:
Отже, енергія точки в коливальному русі пропорційна квадрату амплітуди і квадрату частоти. Якщо система ізольована від інших зовнішніх впливів і точка коливається без тертя, то згідно з законом збереження енергія Е коливального руху точки залишається сталою. Практично всяке коливання матеріальної точки, якщо воно не підтримується ззовні, затухає, його амплітуда з часом зменшується. Причинами затухання коливань є сила тертя в точці, де підвішене тіло, сила опору середовища, передавання коливань іншим тілам, теплові ефекти в деформаціях пружин. Найістотніше впливає на коливання тіла опір середовища. Коли швидкість руху тіла мала, сила опору середовища пропорційна швидкості:
де r – коефіцієнт опору. Знак мінус показує, що сила опору завжди напрямлена проти руху. Визначимо зміщення як функцію від часу у випадку затухаючих коливань. На точку в коливальному русі діють квазіпружна сила і сила опору, тому основне рівняння динаміки має такий вигляд:
Масу m, коефіцієнт пружності k і коефіцієнт опору г називають параметрами коливальної системи. Поділивши рівняння (1) на масу m і ввівши заміну
дістанемо однорідне диференціальне рівняння другого порядку:
Слід відзначити, що частота w0 являє собою частоту власних коливань без тертя, її називають власною частотою осцилятора. Коефіцієнт b – коефіцієнт затухання. За умовою b < w0 рівняння (2) описує затухаючи коливання. Його розв’язок має вигляд:
де А0 – амплітуда коливань у момент початку спостережень, а
З останнього виразу визначаємо умовний період затухаючого коливання:
Характеристики затухання: - час релаксації – це час, за який амплітуда коливань зменшиться в e разів. Оскільки
то
- логарифмічний декремент затухання – логарифм відношення двох послідовних амплітуд:
Якщо замість b підставити його значення, то дістанемо:
- добротність коливальної системи визначається за формулою Щоб коливання не затухали, до системи треба підводити енергію ззовні. Енергію можна поповнювати додатковими зовнішніми поштовхами в такт коливанням. Практично використовуються такі пристрої, за допомогою яких сама коливальна система в потрібний момент зумовлює зовнішній поштовх. Таку систему називають автоколивальною, а її коливання – автоколиваннями. Прикладом автоколивальної системи є годинник. Незатухаючі коливання, що виникають під дією зовнішньої періодично змінної сили, називають вимушеними. Нехай зовнішня сила змінюється за гармонічним законом:
Складемо рівняння динаміки вимушених коливань. При цьому врахуємо, що крім змушувальної сили на систему діють також квазіпружна сила і сила опору середовища, яка пропорційна швидкості руху. Основне рівняння динаміки буде мати такий вигляд:
Поділивши це рівняння на масу і ввівши позначення:
дістанемо неоднорідне лінійне диференціальне рівняння другого порядку:
Досвід показує, що через деякий час у системі встановляться гармонічні коливання з частотою змушувальної сили, які відстають по фазі від останньої на j:
Задача полягає в знаходженні А і j. Для цього продиференціюємо рівняння (5) два рази:
Підставивши рівняння (5), (6) і (7) у (4), одержуємо:
Записавши рівняння (8) для моментів часу, коли
Отже, вирази (5), (9) і.(10) цілком визначають зміщення вимушених коливань. З отриманих рівнянь свідчить: - вимушені коливання є гармонічні коливання, частота яких дорівнює частоті змушувальної сили; -
Підставивши це значення частоти в (0), знайдемо резонансне значення амплітуди:
З отриманих виразів свідчить, що коли опір середовища малий
У цьому випадку амплітуда вимушених коливань стає дуже великою. Залежність амплітуди вимушених коливань від частоти і коефіцієнта затухання зображено на рисунку. Із зростанням коефіцієнта затухання b максимум резонансної кривої швидко опускається і крива згладжується. Явище резонансу стає малопомітним.
|
||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 Для визначення характеру руху механічної системи необхідно, використовуючи закони динаміки або збереження енергії, отримати рівняння руху системи, і якщо воно приводиться до вигляду
Для визначення характеру руху механічної системи необхідно, використовуючи закони динаміки або збереження енергії, отримати рівняння руху системи, і якщо воно приводиться до вигляду  , то можна однозначно твердити, що дана система є гармонічним осцилятором, частота w0 якого дорівнює квадратному кореню з коефіцієнта при х. Розглянемо декілька прикладів і потім узагальнимо отримані результати.
, то можна однозначно твердити, що дана система є гармонічним осцилятором, частота w0 якого дорівнює квадратному кореню з коефіцієнта при х. Розглянемо декілька прикладів і потім узагальнимо отримані результати. (5)
(5) , (6)
, (6) ,
, .
.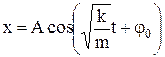

 .
. Отже, кулька, підвішена на пружині й виведена з положення рівноваги, перебуватиме в гармонічному коливанні. Характерно, що її коливання не залежить від сили тяжіння, а лише від повертаючої сили пружності, тому вони будуть однаковими в усіх місцях на Землі і навіть на інших планетах.
Отже, кулька, підвішена на пружині й виведена з положення рівноваги, перебуватиме в гармонічному коливанні. Характерно, що її коливання не залежить від сили тяжіння, а лише від повертаючої сили пружності, тому вони будуть однаковими в усіх місцях на Землі і навіть на інших планетах. :
: ,
,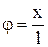 – кутове відхилення маятника.
– кутове відхилення маятника. зрівноважується реакцією нитки. При малих кутових відхиленнях sinj»j, тому повертаючу силу можна записати у вигляді:
зрівноважується реакцією нитки. При малих кутових відхиленнях sinj»j, тому повертаючу силу можна записати у вигляді: ,
, , отримуємо:
, отримуємо: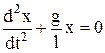 ,
, .
. .
. Фізичний маятник. Фізичним маятником називають тверде тіло довільної форми, яке коливається під дією тяжіння навколо горизонтальної вісі. Якщо маятник вивести з положення рівноваги, то на нього діятиме повертаючий момент М сили тяжіння, знак якого протилежний знаку кута відхилення маятника, а саме:
Фізичний маятник. Фізичним маятником називають тверде тіло довільної форми, яке коливається під дією тяжіння навколо горизонтальної вісі. Якщо маятник вивести з положення рівноваги, то на нього діятиме повертаючий момент М сили тяжіння, знак якого протилежний знаку кута відхилення маятника, а саме: ,
, (рад) повертаючий момент
(рад) повертаючий момент 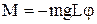 . Цей момент надає тілу кутового прискорення:
. Цей момент надає тілу кутового прискорення: .
. ,
,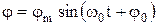

 .
. .
. .
. і коефіцієнт квазіпружної сили
і коефіцієнт квазіпружної сили  , то потенціальну енергію точки в коливальному русі можна визначити за формулою:
, то потенціальну енергію точки в коливальному русі можна визначити за формулою: .
. .
. ,
, .
. ,
, . (1)
. (1) і
і  ,
, . (2)
. (2) ,
,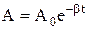 – рівняння залежності амплітуди коливань від часу.
– рівняння залежності амплітуди коливань від часу. 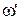 – частота затухаючих коливань, яка визначається за формулою:
– частота затухаючих коливань, яка визначається за формулою: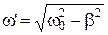 .
. .
.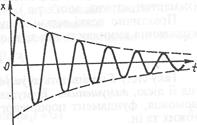 Період називається умовним тому, що затухаючі коливання лише умовно можна вважати періодичними – внаслідок зменшення амплітуди коливання повторюються не абсолютно точно. Період коливання тіла у в'язкому середовищі більший, ніж період його власного коливання. Коли опір середовища значний, коливання не виникає, зміщене тіло повільно без коливання повертається в положення рівноваги. Графік затухаючих коливань зображено на рисунку.
Період називається умовним тому, що затухаючі коливання лише умовно можна вважати періодичними – внаслідок зменшення амплітуди коливання повторюються не абсолютно точно. Період коливання тіла у в'язкому середовищі більший, ніж період його власного коливання. Коли опір середовища значний, коливання не виникає, зміщене тіло повільно без коливання повертається в положення рівноваги. Графік затухаючих коливань зображено на рисунку. і
і  ,
, ;
; .
. ;
; . Визначає якість коливальної системи.
. Визначає якість коливальної системи. .
. (3)
(3) ,
, (4)
(4) (5)
(5) (6)
(6) (7)
(7) (8)
(8) і
і  , отримуємо систему з двох рівнянь, розв’язуючи які одержуємо:
, отримуємо систему з двох рівнянь, розв’язуючи які одержуємо: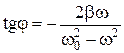 (9)
(9) (10)
(10) амплітуда вимушених коливань залежить не тільки від амплітудного значення змушувальної сили, а й від її частоти коливання. При певній частоті змушувальної сили wрез амплітуда вимушених коливань різко зростає, досягаючи максимального значення. Це явище називається резонансом. Резонансну частоту можна визначити з умови максимуму амплітуди або мінімуму підкореневого виразу в знаменнику рівняння (10):
амплітуда вимушених коливань залежить не тільки від амплітудного значення змушувальної сили, а й від її частоти коливання. При певній частоті змушувальної сили wрез амплітуда вимушених коливань різко зростає, досягаючи максимального значення. Це явище називається резонансом. Резонансну частоту можна визначити з умови максимуму амплітуди або мінімуму підкореневого виразу в знаменнику рівняння (10): .
. .
. , резонансна частота збігається з частотою власних коливань:
, резонансна частота збігається з частотою власних коливань: .
.


