Производственная функция: понятие, виды.

Экономическая деятельность фирмы может быть описана производственной функцией:

Q = f (F1, F2, …, Fn),

где Q – max объем пр-ва при заданных затратах;

F1,2,…, n – кол-во использованного фактора 1, 2,…, n.

Можно представить производственную функцию в таком виде:

Q = f (К, L, M, nt, N),

где K – капитал;

L – труд;

M – материалы;

nt – технический прогресс;

N – нормальная прибыль.

Производственная функция отражает зависимость между объемом применяемых фирмой ресурсов и максимально возможным выпуском продукции, произведенной в определенное время. Онаописывает множество технически эффективных способов производства.

Свойства производственной функции:

1) каждая производственная функция характеризует ту или иную технологию;

2) если меняется технология, то меняется производственная функция;

3) если отсутствует хотя бы один фактор производства, то выпуск продукции невозможен;

4) если фирма увеличивает применение одного ресурса при неизменном количестве других ресурсов или увеличивает использование всех ресурсов, то это – расширение производства по данной технологии.

Двухфакторную модель производственной функции разработали (1927г.) сенатор штата Иллинойс Пол Дуглас и математик Чарльз Кобба. Поэтому она получила название функция Кобба-Дугласа.

Q = AKα L β

или

Y = AKα L 1- α

где А – положительный параметр, измеряющий производительность существующей технологии. Он показывает пропорциональное изменение всей функции. Меняется раз в 30 – 40 лет;

α – постоянная от 0 до 1, измеряющая долю капитала в доходе;

β – доля труда в доходе.

Коэффициенты α и β – это коэффициенты эластичности производства, они показывают, как изменится объем выпуска при изменении труда и капитала на 1%.

Если изменяется только один фактор производства (труд), то такой период является краткосрочным.

Отношение дохода труда к доходу капитала [(1 – α)/ α] постоянно, что и обнаружил Дуглас. Доли факторов производства зависят только от параметра α и не зависят ни от количества факторов, ни от уровня применяемой технологии.

На основе анализа коэффициентов эластичности производства функции Кобба-Дугласа выделяют:

1) пропорционально-возрастающую производственную функцию, т.е. α + β = 1;

2) непропорционально-возрастающую производственную функцию, т.е. α + β > 1;

3) убывающую производственную функцию, т.е. α + β < 1.

Рис.6.1. Производственная функция

От 0 до точки А наблюдается возрастание непропорциональное (от С до В), затем пропорциональное (от В до А), а потом убывание. В точке С высокая скорость функции. В точке В идет угасание функции.

Таким образом, от точки Qc до Qв наблюдается наибольшая отдача от труда. В точке В приближаемся к максимальной отдаче, но прирост отдачи незначителен, что связано с техническими особенностями производства.

Соединим теперь изокосту и карту изоквант (тема 6, п. 1) на одной диаграмме (рис. 7-3):

Рис. 7-3. Экономически эффективный выпуск

 

На рисунке помещены три изокванты и одна изокоста. Напомним, что изокванта отражает все комбинации труда и капитала, при которых выпуск остается неизменным. При этом изокванта, расположенная выше и правее предыдущей, соответствует большему объему выпуска. Объемы выпуска (q1, q2, q3) приведены рядом с соответствующей изоквантой. В свою очередь, изокоста отражает все комбинации труда и капитала, доступные фирме при данных совокупных затратах и ценах труда и капитала.

 

Отсюда вытекает, что в т. А, В и С выпуск одинаков, ибо все они находятся на одной изокванте. При этом совокупные затраты в т. А и С тоже равны, поскольку эти точки принадлежат одной изокосте. В т. В затраты ниже, т.к. она предполагает использование меньшего количества труда и капитала, т.е. принадлежит более «низкой» изокосте, не изображенной на рисунке.

 

Нас, однако, интересует, какой максимальный выпуск достижим при заданных совокупных затратах. Искомый выпуск – q2 – определяется точкой касания изокосты и самой высокой из доступных изоквант (т. Е). Для его достижения фирма должна использовать

труда и

 

капитала. При всех иных доступных фирме комбинациях факторов производства выпуск будет меньше, поскольку в этих случаях фирма окажется на более «низких» изоквантах. В то же время более «высокие» изокванты – например изокванта q3 – расположены выше изокосты, а, значит, недоступны фирме при данных совокупных затратах и ценах труда и капитала.

Итак, применяя

труда и

 

капитала, фирма максимизирует производство при заданных затратах. Поэтому т. Е, соответствующая данной комбинации труда и капитала, называется точкой оптимальной комбинации факторов производства.

 

Напомним, что все точки на любой изокванте (например, на изокванте q2) отражают различные технически эффективные способы производства данного объема продукции (тема 6, п. 1). Но только в т. Е выпуск q2 получается с минимально возможными затратами. Таким образом, комбинация ,

отражает экономически эффективный способ производства продукции в объеме q2.

 

Вспомним также, что в любой точке на изокванте предельная норма технической замены капитала трудом равна отношению предельных продуктов труда и капитала, т.е. выполняется равенство (тема 6, п. 2):

 

В то же время, в точке оптимальной комбинации факторов производства предельная норма технической замены равняется еще и отношению цен труда и капитала. Иными словами, указанное равенство принимает вид:

 

Обосновать это можно так. Пусть в некоторой точке на изокванте предельный продукт труда составляет 10 единиц определенного продукта, а предельный продукт капитала равен 5 единицам. Отношение предельных продуктов равно, следовательно, 2:1. При этом цены труда и капитала, допустим, равны, т.е. соотношение цен составляет 1:1. Таким образом, имеет место неравенство:

 

 

В результате, отказываясь от одной единицы капитала, фирма теряет 5 единиц выпуска. Однако на сэкономленные деньги она может нанять еще одну единицу труда, что принесет ей дополнительно 10 единиц выпуска. В таких условиях, заменяя капитал трудом, фирма увеличивает свой выпуск при неизменных затратах, т.е. переходит на более высокую изокванту, оставаясь на той же изокосте. Фирма будет, следовательно, заменять капитал трудом до тех пор, пока не достигнет точки оптимальной комбинации факторов, которой соотношения предельных продуктов и цен труда и капитала не сравняются друг с другом.[1]

 

Теперь представим, что фирма оказалась в той точке на изокванте, где отношение предельных продуктов труда и капитала меньше соотношения их цен. В этом случае, ей становится выгодно заменять труд капиталом, опять-таки вплоть до достижения точки оптимальной комбинации факторов.

 

Пойдем дальше. Пусть оптимальная комбинация труда и капитала достигнута. Если фирма увеличивает свои затраты, изокоста смещается вправо – вверх. Соответственно точками оптимума последовательно становятся E1, E2, E3 на все более высоких изоквантах. Соединив эти точки, получаем линию «путь развития»

(рис. 7-4).

Рис 7-4. Линия «путь развития»

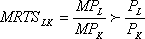
Изменение наклона этой линии говорит о том, использование какого фактора относительно возрастает при увеличении производства.