Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Крайові задачі для рівнянь еліптичного типу.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Дослідження стаціонарних процесів різної фізичної природи (коливання, теплопровідність та інші) часто зводять до рівнянь еліптичного типу:
де Для цих рівнянь зазвичай ставляться лише крайові задачі, оскільки задача Коши, як правило, виявляється некоректною [2], тобто дуже малі зміни початкових даних можуть спричинити істотні зміни розв’язку. Найбільш часто зустрічаються такі крайові задачі.
Перша крайова задача. На контурі задана неперервна функція
що задовольняє всередині області рівнянню (1.1) і приймає на межі
 задані значення, тобто мають задані значення, тобто мають
0 x Така крайова задача для рівняння Мал. 1.1 (1.1) має назву задачі Діріхлє.
Друга крайова задача. На контурі
У цьому випадку крайова задача для рівняння (1.1) має назву задачі Неймана.
Третя крайова задача. На контурі
де Третю крайову задачу можна розв’язати як загальну. Дійсно, при
Метод граничних елементів. Для розв’язку ряда задач достатньо визначити шукані величини тільки на межі досліджуваної області, що знижує розмірність розглядуваних задач. Одним з найбільш широко використаних чисельних методів, що дозволяють вирішити дану проблему, є МГЕ, суть якого полягає у слідуючому. Нехай U0 – точний розв’язок рівняння Лапласа на області
що задовольняє граничним умовам.
( Точний розв’язок U0 може бути знайдено тільки для небагатьох (до того ж простих) випадків, тому, як правило, розв’язок треба апроксимувати. Отже, отримаємо наближений вираз для функції U, тобто розв’язок, підстановка якого в (2.1) і (2.2) порушить указані рівності:
де Таким чином, для розглядуваної області
Тепер головне завдання – зробити ці помилки якнайменшими як у розглядуваній області, так і на межі. Для цього розподілимо функцію помилок наступним чином згідно з [1]:
де
Співвідношення (2.5) можна записати в іншому вигляді, використовуючи вираз (2.4):
Вагова функція
на всій площині
Інтегруючи співвідношення (2.7) два рази за частинами та враховуючи (2.8), отримаємо
Тут Якщо контур
причому на кожному елементі Ui і qj вважаємо постійними
В якості вагової функції розглянемо фундаментальний розв’язок рівняння Лапласа
Оскільки рівняння (2.10) однорідне, коефіцієнт перед логарифмом можна відкинути. Координати джерела Координати джерела можна обчислити за формулами
Підставляючи вагову функцію (2.11) у (2.10), отримаємо систему лінійних алгебраїчних рівнянь, коефіцієнти якої є криволінійні інтеграли першого роду, обчислювані для кожного елемента. Для обчислення значення U у внутрішній точці i області
яке зв’язує значення функції U в точці i зі значенням q і U на межі У формулі (2.13) Примітка. Для визначення
1. Коли нормаль направлена до центру кола, рівняння кола
знаходимо
складемо допоміжну функцію
Тоді
2. Якщо нормаль направлена від центру, рівняння кола запишеться
Подальші міркування аналогічні наведеним у п. 1. Отримаємо
Приклад 2.1. Розглянемо задачу теплопровідності для контура (мал. 2.1), де на сторонах L1, L2, L4, L5 – задана температура, а на сторонах L3, L6 – задано тепловий потік. Математична формуліровка задачі має вигляд
Тоді за контур
Враховуючи
отримаємо
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.254.202 (0.01 с.) |

 (1.1)
(1.1) та
та 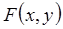 - неперервні функції.
- неперервні функції. , що обмежує область
, що обмежує область 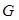 (мал. 1.1),
(мал. 1.1), .
.

 y Потрібно знайти функцію
y Потрібно знайти функцію  ,
,
 виконуватися умови
виконуватися умови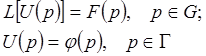 (1.2)
(1.2)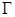 , що обмежує область
, що обмежує область  , задана неперервна функція
, задана неперервна функція  . Потрібно знайти функцію
. Потрібно знайти функцію  , що задовольняє всередині
, що задовольняє всередині  рівнянню (1.1), нормальна похідна якої на
рівнянню (1.1), нормальна похідна якої на  , тобто потрібно, щоб виконувалися умови
, тобто потрібно, щоб виконувалися умови (1.3)
(1.3)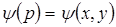 . Потрібно знайти функцію
. Потрібно знайти функцію  таку, щоб виконувалися умови
таку, щоб виконувалися умови , (1.4)
, (1.4) .
. та
та  отримаємо першу, а при
отримаємо першу, а при  та
та  – другу крайову задачу. Помітимо, що якщо область
– другу крайову задачу. Помітимо, що якщо область 
 , (2.1)
, (2.1) (2.2)
(2.2)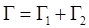 – повна межа розглядуваної області
– повна межа розглядуваної області  ).
). (2.3)
(2.3)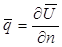 .
.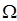 та її межи
та її межи  (2.4)
(2.4) , (2.5)
, (2.5) – вагова функція;
– вагова функція; . (2.6)
. (2.6) . (2.7)
. (2.7) – повинна бути неперервною разом зі своїми другими похідними та задовольняти рівнянню
– повинна бути неперервною разом зі своїми другими похідними та задовольняти рівнянню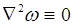 (2.8)
(2.8) . (2.9)
. (2.9) і
і  – шукані, а
– шукані, а  і
і  – задані.
– задані. розбити на скінчене число граничних елементів K1+K2, тобто
розбити на скінчене число граничних елементів K1+K2, тобто ,
, , то рівняння (2.9) матиме вигляд
, то рівняння (2.9) матиме вигляд . (2.10)
. (2.10)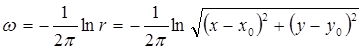 . (2.11)
. (2.11)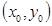 обираємо не на контурі, а на відстані
обираємо не на контурі, а на відстані  на зовнішній нормалі, де d – довжина елемента.
на зовнішній нормалі, де d – довжина елемента. (2.12)
(2.12)
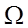 використовується співвідношення [1]
використовується співвідношення [1]
 , (2.13)
, (2.13) .
. – задані, q, U – знайдені величини, а
– задані, q, U – знайдені величини, а  – фундаментальний розв’язок (2.11), в якому за джерело
– фундаментальний розв’язок (2.11), в якому за джерело  береться внутрішня точка
береться внутрішня точка  .
. і
і  , де n – нормаль до кола, можна отримати формули для двох випадків.
, де n – нормаль до кола, можна отримати формули для двох випадків. (тут (a, b) – координати центру, R – радіус кола) перепишемо у вигляді
(тут (a, b) – координати центру, R – радіус кола) перепишемо у вигляді ;
;


 .
.


 y
y


 2 L2
2 L2



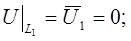 L3 L1
L3 L1 1 L4 L6
1 L4 L6

 0 1 L5 3 4 x
0 1 L5 3 4 x Мал. 2.1
Мал. 2.1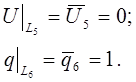
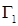 приймаємо суму L1+L2+L4+L5, а за контур
приймаємо суму L1+L2+L4+L5, а за контур  - суму L3+L6. Граничне рівняння має вигляд
- суму L3+L6. Граничне рівняння має вигляд
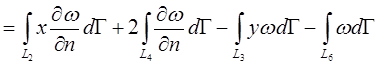 (*)
(*) ,
, ;
;