
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
До задачі з однорідними граничними умовами.Содержание книги Поиск на нашем сайте 1.Розглянемо задачу про поширення тепла в теплоізольованомустержні, на кінцях якого підтримується постійна температура
крайові умови:
і початкові умови:
Труднощі цієї задачі полягають у тому, що оскільки крайові умови неоднорідні, то не можна розв’язувати її методом поділення змінних. Але очевидно, що при t
У цьому випадку ставиться задача знаходження перехідної температури
Підставимо (2.2) у граничні умови задачі (2.1). Враховуючи (2.3), знайдемо величини А і В. Тепер задачу (2.1) можна розв’язати відносно нової невідомої функції V(x,t) і додати її до стаціонарного розв’язку. Отже в результаті одержимо шукану функцію V(x,t). Оформлюємо задачу відносно функції V(x,t). Для цього функцію (2.2) підставимо в рівняння та у граничні та початкові умови, тоді нова задача буде:
Таким чином, одержали задачу не тільки з однорідним рівнянням, а й з однорідними граничними умовами, що дозволяє розв’язати її методом поділення змінних.
2. Перетворення неоднорідних граничних умов, які залежать від змінної t, в однорідні. Розглянемо типову задачу:
Для перетворення цих граничних умов у нульові виберемо розв’язок задачі у такій формі:
де функції A(t) та B(t) вибирають такими, щоб
задовольняло неоднорідним граничним умовам задачі (2.4). у цьому випадку функція V(x,t) буде задовольняти аналогічним, тільки однорідним, граничним умовам. Підстановка функції S(x,t) у граничні умови
зводить до двох рівнянь, з яких можна визначити A(t) і B(t). В результаті отримаємо
Отже,
Якщо підставити вираз (2.8) для U(x,t) в рівняння, граничні та початкові умови задачі (2.4), то одержимо нову задачу для невідомої функції V(x,t):
Маємо нову задачу з однорідними граничними умовами, але рівняння стало неоднорідним. У цьому випадку задачу можна розв’язати методом інтегральних перетворень або скористатися розвиненням у ряд по власним функціям.
Зауваження: 1.Лінійні неоднорідні граничні умови загального виду
також можна перетворити в однорідні граничні умови. Очевидно, що нове рівняння, в цьому випадку, буде неоднорідним. 2.Деякі методи розв’язку задач не мають ніяких вимог до однорідності граничних умов, отже, у такому випадку, не треба їх і перетворювати в однорідні.
Метод поділення змінних. (Метод Фур’є). Сутність методу – розклад шуканого розв’язку на добуток найпростіших компонент. Метод поділення змінних вживається у таких випадках: 1.Рівняння лінійне й однорідне (не обов’язково з постійними коефіцієнтами). 2.Граничні умови задаються у вигляді:
де
Загальні принципи метода поділення змінних. Для найпростішого рівняння з частинними похідними поділення змінних – це пошук розв’язку у вигляді:
де X(x) – функція, залежна від змінної х; T(t) – функція, залежна від змінної t. Необхідно знайти нескінченне число таких розв’язків рівняння з частинними похідними, які задовольняють граничним умовам. Ці найпростіші функції
Розв’язок задачі U(x,t) знаходиться у вигляді лінійної комбінації фундаментальних розв’язків
яка задовольняє початковим умовам. І оскільки ця сума задовольняє рівнянню і граничним умовам, вона є розв’язком вихідної задачі.
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 і
і  , тобто маємо рівняння у частинних похідних:
, тобто маємо рівняння у частинних похідних: , (2.1)
, (2.1)

 розв’язок задачі наближається до стаціонарного, яке лінійно змінюється (вздовж осі OX) від температури K1 до температури K2. Інакше припустимо, що температуру у цій задачі можна подати у вигляді суми двох доданків: стаціонарного (граничного розв’язку для великих значень аргументу t) і перехідного, тобто частини розв’язку, яка залежить від початкових умов і зі збільшенням змінної t наближається до нуля, або
розв’язок задачі наближається до стаціонарного, яке лінійно змінюється (вздовж осі OX) від температури K1 до температури K2. Інакше припустимо, що температуру у цій задачі можна подати у вигляді суми двох доданків: стаціонарного (граничного розв’язку для великих значень аргументу t) і перехідного, тобто частини розв’язку, яка залежить від початкових умов і зі збільшенням змінної t наближається до нуля, або (2.2)
(2.2) . Припустимо, що функція
. Припустимо, що функція  задовольняє однорідним граничним умовам:
задовольняє однорідним граничним умовам: (2.3)
(2.3)



 (2.4)
(2.4)
 , (2.5)
, (2.5) (2.6)
(2.6)
 (2.7)
(2.7)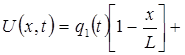
 +
+  (2.8)
(2.8) - неоднорідне рівняння у частинних похідних
- неоднорідне рівняння у частинних похідних - однорідні граничні умови
- однорідні граничні умови - початкові умови
- початкові умови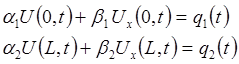
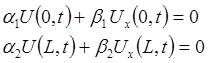 ,
,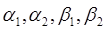 – константи (такі граничні умови називаються лінійними однорідними).
– константи (такі граничні умови називаються лінійними однорідними).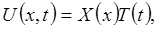
 називаються фундаментальними розв’язками.
називаються фундаментальними розв’язками. тобто вислідна суми
тобто вислідна суми



