
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поділення змінних у задачі теплопровідності стержня з теплоізольованою бічною поверхнею.Содержание книги
Поиск на нашем сайте
Знайти функцію U(x,t), яка є розв’язком задачі
де Будемо шукати розв’язок у вигляді:
Підставимо (3.4) в рівняння (3.1), одержимо:
Поділимо обидві частини останнього рівняння на
У цьому виразі змінні поділені, тобто ліва частина рівняння залежить від t, а права – тільки від x. І оскільки x і t незалежні одне від одного, то кожна частина цього рівняння повинна бути константою. Позначимо її через k, тоді
або
Тепер можна розв’язати кожне з цих звичайних диференціальних рівнянь. Добуток відповідних розв’язків буде задовольняти вихідному рівнянню з частинними похідними. Слід звернути увагу на ту обставину, що константа k повинна бути від’ємною (у протилежному випадку рівняння
Виходячи з цього, позначимо
Ці рівняння є однорідними рівняннями стандартного типу з постійними коефіцієнтами. Їх загальні розв’язкі мають вигляд
де Підставляючи в добуток X(x)T(t) одержані вирази і об’єднуючи сталі, одержимо функцію виду
яка задовольняє рівнянню у частинних похідних. Треба підкреслити, що знайшли нескінченний набір функцій, які задовольняють вихідному рівнянню з частинними похідними.
Знаходження розв’язків, які задовольняють граничним умовам. Таким чином, маємо безліч розв’язків вихідного рівняння, але не всі вони задовольняють граничним та початковим умовам. Треба вибрати таку підмножину розв’язків виду (3.5), яка б задовольняла граничним умовам (3.2). Для цього підставимо розв’язок (3.5) у ті граничні умови:
Отже маємо задачу:
яка називається задачею Штурма-Ліувіля. Розв’язок цієї задачі дає В= 0 і отож
Таким чином, одержали числа, які називаються власними. Вони володіють такими властивостями: а) множина власних значень – лічильна; б) всі власні числа невід’ємні; в) якщо власні значення розташувати у порядку зростання
то г) всі власні значення задачі Штурма-Ліувіля – прості, тобто кожному власному значенню відповідає одна власна функція Отже маємо нескінчений набір розв’язків
кожен з яких задовольняє рівнянню з частинними похідними та граничним умовам. Розв’язок вихідної задачі є сума цих найпростіших функцій.
Пошук розв’язку, який задовольняє рівнянню, граничним та початковим умовам. Треба знайти суму фундаментальних розв’язків
з такими коефіцієнтами Ck, щоб функція U(x,t) задовольняла початковій умові
Якщо підставити (3.8) у (3.7), то будемо мати
Вираз (3.9) є звичайним розкладом функції у ряд Фур’є. Коефіцієнти ряду знаходяться по формулі:
Таким чином, знайшли розв’язок задачі (3.1) – (3.3), який має вигляд:
Поширення тепла у стержні. Задача. Нехай на лівому кінці стержня з теплоізольованою бічною поверхнею підтримується постійна температура, яка дорівнює 2 одиницям, а на правому кінці задана теплова течія, яка дорівнює 5. Початковий розподіл температури показаний на малюнку 4.1. Проведемо дослідження з часом зміни цього розподілу.
0
Мал. 4.1 З малюнка легко вивести аналітичну форму функції U(x,0)=f(x), яка буде
Процес поширення тепла у стержні описується рівнянням
причому, відповідно заданому тепловому режиму на кінцях стержня
Таким чином, задача зводиться до розв’язку диференціального рівняння (4.2) при граничних (4.3) і початкових (4.1) умовах. Для зручності подальших викладок перейдемо до безрозмірних величин:
Враховуючи, що
рівняння (4.2) та умови (4.1) і (4.3) перепишемо у вигляді
Оскільки у даній задачі граничні умови неоднорідні, то безпосередньо вживати метод поділення змінних не можна. Неоднорідні граничні умови потрібно перетворити в однорідні. Для цього будемо шукати розв’язок задачі у формі
де
Підставимо (4.7) в (4.8), отримаємо
Тоді співвідношення (4.8) приймає вигляд:
або
Сформулюємо вихідну задачу відносно функції
Далі розв’язуємо рівняння методом Фур’є, тобто розв’язок шукаємо у формі
Розв’язок (4.14) підставляємо у рівняння (4.11).
Поділимо праву та ліву частини рівності на
Остання рівність можлива лише у тому випадку, коли обидві частини не залежать від
Розв’яжемо ці рівняння і підставимо в (4.14), тоді будемо мати
де Отже отримали загальний розв’язок рівняння (4.11). Для знаходження частинного розв’язку з граничних та початкових умов визначимо константи. З граничних умов задачі Штурма-Ліувілля маємо
отже
Власними функціями є
Оскільки одержане число
Цей розв’язок рівняння (4.11) задовольняє граничним умовам (4.12) і для кожного значення Тому слід надати константі індекс
Сума розв’язків (4.19) буде також розв’язком рівняння (4.11), тому що розв’язки складають лінійно-незалежну фундаментальну систему. Таким чином
Для визначення довільної константи
Остання формула показує, що константи
Підставимо вираз (4.15) для функції
Виконав необхідні обчислення, дістанемо
Підставимо (4.21) в (4.20) і, враховуючи рівність (4.9), запишемо остаточний розв’язок задачі:
Нехай
Мал.4.2
З цих вислідів видно, що наявність течії на одному кінці стержня і постійної додатної температури на другому, призводять до явища, коли стержень охолоджується з часом дуже повільно.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.21 (0.007 с.) |

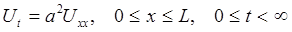 (3.1)
(3.1) (3.2)
(3.2) (3.3)
(3.3)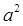 – постійна величина.
– постійна величина. (3.4)
(3.4)

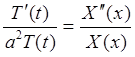



 з граничними умовами X(0)=0 і X(L)=0 має тільки розв’язок X(x)=0, тобто функція T(t) повинна наближатися до нуля при t
з граничними умовами X(0)=0 і X(L)=0 має тільки розв’язок X(x)=0, тобто функція T(t) повинна наближатися до нуля при t  ).
). , де
, де  не може дорівнювати нулю, оскільки тоді розв’язок буде тривіальним. Отже вираз “-
не може дорівнювати нулю, оскільки тоді розв’язок буде тривіальним. Отже вираз “-  ” буде завжди від’ємним. З урахуванням нового позначення для константи маємо два звичайних диференціальних рівняння першого і другого порядків:
” буде завжди від’ємним. З урахуванням нового позначення для константи маємо два звичайних диференціальних рівняння першого і другого порядків:

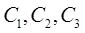 – довільні сталі.
– довільні сталі. , (3.5)
, (3.5)
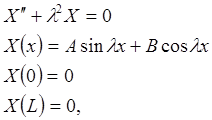
 , але
, але  , оскільки тоді
, оскільки тоді  ,
, .
. ,
,
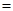
 ;
; .
. (3.6)
(3.6) (3.7)
(3.7)
 (3.8)
(3.8) (3.9)
(3.9)
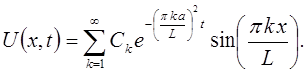 (3.10)
(3.10)













 (4.1)
(4.1) , (4.2)
, (4.2) (4.3)
(4.3) (4.4)
(4.4) ;
;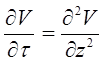 (4.5)
(4.5) (4.6)
(4.6)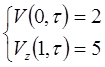 (4.7)
(4.7) (4.8)
(4.8) - функція, яка задовольняє однорідним граничним умовам, аналогічним (4.7);
- функція, яка задовольняє однорідним граничним умовам, аналогічним (4.7); - лінійна функція, яка задовольняє неоднорідним граничним умовам.
- лінійна функція, яка задовольняє неоднорідним граничним умовам.
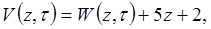 (4.9)
(4.9)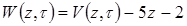 . (4.10)
. (4.10)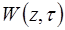 . Для цього (4.9) підставимо в (4.5). Отже задача буде
. Для цього (4.9) підставимо в (4.5). Отже задача буде (4.11)
(4.11) (4.12)
(4.12) (4.13)
(4.13) (4.14)
(4.14)
 , отримаємо
, отримаємо (4.15)
(4.15) і
і  ,тобто є постійними величинами. Позначимо її через
,тобто є постійними величинами. Позначимо її через 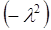 . Тоді з рівності (4.15) одержимо два звичайних диференціальних рівняння
. Тоді з рівності (4.15) одержимо два звичайних диференціальних рівняння (4.16)
(4.16) (4.17)
(4.17) (4.18)
(4.18)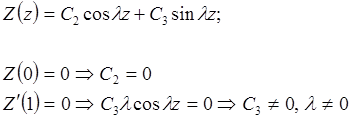

 .
. залежить від
залежить від  , яке змінюється до нескінченності, то кожному значенню
, яке змінюється до нескінченності, то кожному значенню  буде відповідати розв’язок
буде відповідати розв’язок
 будемо мати іншу константу.
будемо мати іншу константу. . Тоді розв’язок буде мати вигляд
. Тоді розв’язок буде мати вигляд (4.19)
(4.19) (4.20)
(4.20) , використаємо початкову умову, з якої виходить
, використаємо початкову умову, з якої виходить
 виявляються коефіцієнтами розкладання функції
виявляються коефіцієнтами розкладання функції  у ряд Фур’є по синусам в інтервалі (0,1). Отже
у ряд Фур’є по синусам в інтервалі (0,1). Отже
 під інтеграл, тоді
під інтеграл, тоді
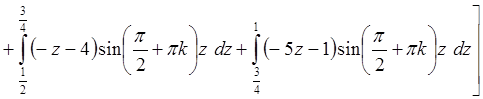 .
.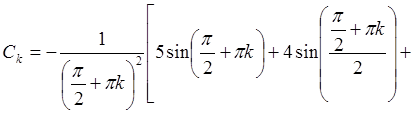
 (4.21)
(4.21) .
.


 (4.22)
(4.22) змінюється від 0 до 1 з кроком 0.2, а
змінюється від 0 до 1 з кроком 0.2, а  - від 0 до 1 з кроком 0.25. Змінення розподілу температури вздовж стержня з часом показано на графіках малюнку 4.2.
- від 0 до 1 з кроком 0.25. Змінення розподілу температури вздовж стержня з часом показано на графіках малюнку 4.2.




