
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування транспортної задачі у відкритій моделіСодержание книги Поиск на нашем сайте
Якщо загальні обсяги запасів і потреб не збалансовані, модель є відкритою. Для перетворення її в закриту модель вводиться умовний (фіктивний) постачальник або споживач з відповідним обсягом запасів (потреб)
Приклад. a 1 = 30; a 2 = 70; a 3 = 70; b1 = 50; b2 = 50; b3 = 40; b4 = 60 С =
Тому що 170 < 200, необхідно ввести додатково умовного постачальника А4 з обсягом товару a 4=200–170=30. Доповнимо матрицю С нульовим рядком; розв’язуємо отриману задачу. Побудуємо опорний план методом подвійної переваги; при цьому нулі останнього рядка матриці С не враховуються при знаходженні мінімумів.
Z = 620 N = 6; m+n-1 = 7 План вироджений, поставимо нуль у (1,1). Розрахуємо потенціали й оцінимо план. План не оптимальний, будуємо цикл перерозподілу з вершиною в клітині (1,2). Перерозподіл фіктивний, нуль переходить у клітину (1,2). min (0; 20;50) = 0
- +
50 -
- +
Оцінимо отриманий план. Після аналогічного кроку одержуємо план
План оптимальний. Z = 620 гр. од. Споживач В4 фактично залишається з дефіцитом у 30 од. Контрольні запитання 1. Яким є загальний алгоритм розв’язування ТЗ? 2. Яким чином слід перетворити вироджений план ТЗ у не вироджений? 3. Як визначаються потенціали постачальників і споживачів? 4. Як формувати цикл перерозподілу постачань для поліпшення плану? 5. Як треба перетворити відкриту модель ТЗ у закриту? Якими можуть бути кінцеві висновки після отримання розв’язку?
Лекція 7
1. Однопродуктова модель поточного планування 2. Однопродуктова модель перспективного планування
1.Однопродуктова модель поточного планування Мається один продукт і
Цільова функція цієї задачі – усі витрачені кошти
Обмеження
Модель з цією умовою називається закритою. Дана задача є задачею лінійного програмування. Через специфіку розв’язується спеціальними методами. Система обмежень має У класичній транспортній задачі передбачається, що пропускна здатність усіх маршрутів досить велика і немає варіантів вибору різних видів транспорту. У реальних економічних задачах з’являються ускладнення: 1. продукт, запланований для перевезення, може бути однотипним (взаємозамінним); 2. на декількох маршрутах можуть бути використані різні види транспорту; 3. на окремих маршрутах можуть бути задані обмеження пропускної здатності. За всіх цих обмежень транспортна задача може бути вирішена симплекс-методом.
2.Однопродуктова задача перспективного планування Зміст: планується виробництво і розподіл одного чи декількох взаємозамінних видів продукції в умовах, коли наявні виробничі потужності недостатні для задоволення попиту. Додатковий елемент планування − уведення нових виробничих потужностей. У постановці задачі змінюються Умови, необхідні для задачі перспективного планування:
Додаткові позначення:
Розв’язання задачі повинне визначити оптимальний варіант розміщення виробництва і перевезень продукції, що забезпечує мінімізацію суми усіх витрат на будівництво, виробництво та перевезення.
Система обмежень:
Відкрита модель транспортної задачі перетвориться в закриту введенням умовного споживача. В оптимальному плані робляться висновки: ті постачальники (виробники), до яких прикріпився умовний споживач, недоцільні для використання. Якщо це проект, то він відкидається як невигідний; якщо це виробництво – рекомендується його закривати. Можливі проблеми − частина потреб умовного постачальника забезпечується реальним виробником, а частина деяким проектом. При розв’язанні доводиться вибирати варіанти, близькі до оптимального. Приклад. Маємо два діючих підприємства А і Б, потужності яких 120 тис. і 180 тис. од. продукції відповідно. Мається 3 споживачі з відповідними обсягами потреб - 155 тис., 130 тис., 390 тис. од. продукції. 120+180=300 тис. од. продукції (потужності); 155+130+180=375 тис. од. продукції (потреби). Планується збільшення виробничих потужностей на 75 тис. од. продукції. Розглянемо два варіанти − реконструкція підприємства Б і будівництво нового підприємства. Задано матрицю наведених витрат на одиницю продукції
Результати розв’язання:
Висновок: реконструкція підприємства Б недоцільна, вигідне будівництво нового підприємства. Потужності проектовані і реконструйовувані можуть бути не фіксованими, а задаватися в деяких інтервалах. У цих інтервалах питомі капітальні витрати і собівартість є змінними. Однак цільова функція може бути збережена в лінійній формі. Контрольні питання
Лекція 8
1. Загальна постановка задачі управління запасами 2. Однопродуктова модель Уїлсона: умови і параметри 3. Оптимальний розв’язок в моделі Уїлсона і його властивості 4. Однопродуктова модель з дефіцитом
Загальна постановки задачі Мається деякий склад для збереження
У моделі без дефіциту витрати двох видів: 1. витрати за замовленням і доставкою товарів; 2. витрати збереження; Задача має тривіальне рішення.
Недоліки цього рішення: 1. склад працює як перевалочна база; 2. неможливість реалізації рішення на практиці: а) для багатьох видів товарів існують мінімальні обсяги партій; б) загальний обсяг може бути занадто великий для одночасної доставки (транспортне обмеження). Висновок: для реального працюючого складу (оптової бази) практично неможливе одноразове завезення за всією номенклатурою товарів. Формулювання однієї з конкретних задач – визначити графік доставки товарів у такій черговості й у такій кількості, щоб при безумовному задоволенні попиту середньої обсяг (рівень) запасів був мінімальним. Математичні методи розв’язання подібних задач створюють теорію управління запасами.
Однопродуктова модель Уїлсона: 1. на складі зберігається один товар (продукт); 2. попит на товар є постійним (рівень запасу товару зменшується з постійною швидкістю) 3. у той момент, коли запас вичерпаний, подається заявка на доставку нової партії товарів; 4. виконання заявки (замовлення) здійснюється миттєво; 5. накладні витрати, пов'язані з замовленням і доставкою товару постійні і не залежать 6. щоденна вартість збереження одиниці товару Схема роботи складу
3.Плануємо роботу складу на деякий період Т Розраховуємо кількість замовлень: Загальні витрати за замовленням і доставкою:
Середній рівень запасу: Витрати на збереження в одному періоді: Загальні витрати на збереження: Загальні витрати в плановому періоді S:
Знайдемо мінімум складеної функції витрат.
Можна перевірити, що Q * - це точка мінімуму:
Висновок: у точці мінімуму витрати збереження дорівнюють витратам на замовлення і доставку.
Знайдемо інтервал між замовленнями.
Практичні труднощі при використанні моделі Уїлсона: 1. теоретична оптимальна величина
2. оптимальне
Напрямки ускладнення моделі Уїлсона: 1. Модель з дефіцитом. 2. 3. Моделі з випадковим попитом 4. Багатопродуктові моделі.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.192.174 (0.01 с.) |




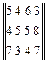


 0 *
0 *
 + 20
+ 20 50 20
50 20 виробників цього продукту,
виробників цього продукту,  ;
;  – відповідно обсяги виробництв продукту. Мається
– відповідно обсяги виробництв продукту. Мається  замовників (споживачів) –
замовників (споживачів) –  ;
; 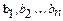 відповідні обсяги потреб у цьому продукті. Задано матрицю
відповідні обсяги потреб у цьому продукті. Задано матрицю  елементи якої – ціни доставки продукту по відповідному маршруті, чи відстані (довжини маршрутів
елементи якої – ціни доставки продукту по відповідному маршруті, чи відстані (довжини маршрутів 
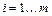 ,
,  . Необхідно скласти план прикріплення споживачів і підприємства-виробників так, щоб потреби були задоволені і загальні транспортні витрати були мінімальними Це найпростіша транспортна задача.
. Необхідно скласти план прикріплення споживачів і підприємства-виробників так, щоб потреби були задоволені і загальні транспортні витрати були мінімальними Це найпростіша транспортна задача. матриця змінних. Зміст – обсяг продукту, що підлягає перевезенню даним маршрутом.
матриця змінних. Зміст – обсяг продукту, що підлягає перевезенню даним маршрутом.


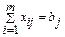

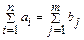 − рівняння балансу
− рівняння балансу
 незалежних рівнянь, з цього випливає, що в оптимальному плані задачі завантажено не більш ніж
незалежних рівнянь, з цього випливає, що в оптимальному плані задачі завантажено не більш ніж  і
і  цілі числа, то оптимальний план містить тільки цілі координати. Якщо модель є відкритою (рівність (5) порушено), вона перетвориться в закриту введенням умовного постачальника чи споживача. Ця модель статична – вибір робиться один раз. Задача планування детермінована та оптимізаційна.
цілі числа, то оптимальний план містить тільки цілі координати. Якщо модель є відкритою (рівність (5) порушено), вона перетвориться в закриту введенням умовного постачальника чи споживача. Ця модель статична – вибір робиться один раз. Задача планування детермінована та оптимізаційна. − не тільки реальні виробничі потужності, але і різні варіанти проектованих потужностей. Якщо на діючому виробництві можлива реконструкція, то вихідна і додаткова потужності показуються окремо.
− не тільки реальні виробничі потужності, але і різні варіанти проектованих потужностей. Якщо на діючому виробництві можлива реконструкція, то вихідна і додаткова потужності показуються окремо. .
. − собівартість одиниці продукції виробника
− собівартість одиниці продукції виробника 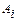 ;
; − питомі капітальні витрати;
− питомі капітальні витрати; − питомі транспортні витрати по відповідному маршруті;
− питомі транспортні витрати по відповідному маршруті; − нормативний коефіцієнт ефективності капітальних вкладень.
− нормативний коефіцієнт ефективності капітальних вкладень.

 ;
;

 ;
;

 найменувань товарів. Відомий щоденний попит на кожен вид товарів
найменувань товарів. Відомий щоденний попит на кожен вид товарів  Відома загальна ємність (місткість) складу
Відома загальна ємність (місткість) складу  . Потрібно визначити процедуру завезення товарів на склад, при якій попит задовольняється і витрати мінімальні. Нехай
. Потрібно визначити процедуру завезення товарів на склад, при якій попит задовольняється і витрати мінімальні. Нехай  – обсяги партій відповідних товарів. Їхню суму позначимо через
– обсяги партій відповідних товарів. Їхню суму позначимо через  ,
, 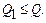
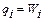
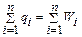
 ;
; від кількості товарів (обсягу партій)
від кількості товарів (обсягу партій)  ;
;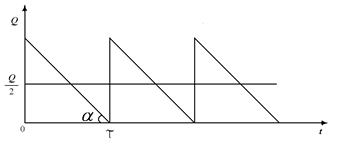
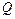 – максимальна кількість товару на складі;
– максимальна кількість товару на складі; 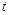 – час;
– час;  – інтервал часу між точками замовлення.
– інтервал часу між точками замовлення. ;
; 
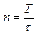 .
.

 .
.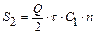
 ,
,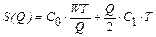
 ;
;  ;
; 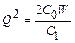 .
.






 не завжди може бути реалізована на практиці. Округлення
не завжди може бути реалізована на практиці. Округлення 
 також може бути практично не реалізованим.
також може бути практично не реалізованим. – змінний детермінований попит.
– змінний детермінований попит.


