
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерії при розв’язуванні ігор із природоюСодержание книги Поиск на нашем сайте
Припустимо, що заздалегідь відомо ймовірності стану природи.
1. Критерієм вибору оптимальної стратегії є максимум математичного сподівання виграшу (можливого виграшу):
Якщо ймовірності невідомі, у деяких задачах використовується принцип недостатньої підстави, за якою усі стани природи є рівно можливими (рівно ймовірними).
2. Критерій Вальда:
3. Критерій мінімального ризику Севіджа: Обидва критерії є песимістичними. 4. Комбінований критерій Гурвіца. Він передбачає розрахунок наступної величини.
Приклад. Можливе будівництво 4 типів електростанції. Ефективність побудованої електростанції залежить від ряду факторів – режиму ріки, вартості палива, вартості доставки палива і т.ін. Припустимо, що виділено чотири різних стани
Матриця ефективності:
Критерій Вальда:
Критерій Севіджа. Побудуємо матрицю ризиків:
Критерій Гурвіца. 1.
2.
Принцип недостатньої підстави Контрольні питання 1. Що називається природою? 2. Що таке стани природи? 3. Які критерії використовуються в іграх з природою? 4. Які реальні економічні задачі моделюються як ігри з природою?
Лекція 14
1. Багатоетапні моделі. Принцип Беллмана 2. Задача розподілу засобів (ресурсів) 3. Задача видобутку корисної копалини
Економіко-математичні моделі називаються динамічними, якщо в них враховується розвиток процесу в часі. Розв’язання таких задач розбивається на ряд етапів(кроків), тому їх називають багатоетапними чи багатокроковими. У процесі розв’язування необхідно знайти послідовність оптимальних впливів (управлінь). Основним принципом розв’язання є принцип Беллмана – якщо деяка послідовність розв’язків оптимальна, то окремі рішення усередині її оптимальні стосовно попереднього рішення. Оптимальна стратегія розв’язання багатоетапної задачі складається з оптимальних рішень для кожного окремого етапу.
Потрібно керувати в моменти Динамічні задачі розв’язуються специфічним чином, починаючи з останнього етапу.
2. Задача розподілу засобів (ресурсів)
Постановка задачі. Маємо деяку кількість коштів Припустимо, є варіант розподілу: y і (x-y) відповідно. Функції прибутковості: Загальний прибуток:
Зміст: найбільше значення на відрізку. Загальна постановка задачі передбачає планування розподілу коштів на кілька етапів. Потрібні додаткові дані. Задано коефіцієнти Розглянемо найпростіший випадок, планування на два етапи. Потрібно порахувати кількість коштів доступних для інвестицій після закінчення першого етапу.
Планується перший етап з урахуванням найкращого другого етапу.
Для трьох етапів:
Приклад.
Потрібно скласти план розподілу коштів на два етапи.
Складемо функцію прибутку:
Вибір найбільшого значення:
Одержали Зберемо прибуток за два етапи, з урахуванням кількості коштів, що залишилися.
Функція прибутку:
– можливий прибуток за перший етап і найкращий за наступний.
Оптимальний план розподілу засобів: на першому етапі всі кошти спрямовуються в перше підприємство, після закінчення етапу кошти, що залишилися, вкладаються в друге підприємство. Ланцюжок керувань Максимальний загальний прибуток
|
||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.100 (0.007 с.) |

 ;
;  .
. .
. ;
;  ;
; 
 – стратегія гарантованого ризику (нижня ціна гри).
– стратегія гарантованого ризику (нижня ціна гри). .
.
 .
. – теплова,
– теплова,  гідроелектростанції за різними проектами:
гідроелектростанції за різними проектами:  – приплотинна,
– приплотинна,  - безшлюзова,
- безшлюзова,  - шлюзова.
- шлюзова. , кожен з яких означає визначене поєднання факторів.
, кожен з яких означає визначене поєднання факторів. .
. рекомендовано проект
рекомендовано проект  .
.
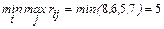 рекомендовано проект
рекомендовано проект 

 рекомендовано варіант
рекомендовано варіант 



 вибираємо
вибираємо  .
.  вибираємо
вибираємо 
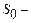 початкова множина станів;
початкова множина станів; деяка множина кінцевих станів
деяка множина кінцевих станів .
. , що можуть бути вкладені в два різних підприємства (проекти). Кожне підприємство відрізняється своїми умовами виробництва і має свою функцію прибутковості. Потрібно розподілити засоби так, щоб загальний прибуток був максимальний.
, що можуть бути вкладені в два різних підприємства (проекти). Кожне підприємство відрізняється своїми умовами виробництва і має свою функцію прибутковості. Потрібно розподілити засоби так, щоб загальний прибуток був максимальний. і
і  .
. .
.

 ,
, 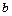 повернення засобів після закінчення етапу,
повернення засобів після закінчення етапу, 
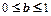 .
.
 – вже отримано.
– вже отримано.











 ,
,  – межові точки.
– межові точки.

 .
. при
при  – для другого етапу.
– для другого етапу.




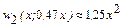
 – найбільше значення.
– найбільше значення.

 .
.


