
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ігри зі змішаними стратегіямиСодержание книги Поиск на нашем сайте
Якщо
Введемо в розгляд два вектори:
Виграш при використанні змішаних стратегій визначається як математичне сподівання виграшу чи як середній виграш.
Виконано рівність:
Теорема: Кожна скінченна гра має, принаймні, один розв’язок, можливо, в області змішаних стратегій.
Розглянемо найпростіший окремий випадок.
3. Якщо сідлівкої точки немає, необхідно застосовувати змішані стратегії. Вводимо в розгляд два вектори ймовірностей.
Система лінійна, може бути вирішена будь-якими способами.
Друга система для ймовірностей
Приклад. Розв’язок гри в змішаних стратегіях
Сідловкої точки немає, тому що
4. Розв’язок гри може бути отриманий геометрично (за допомогою графіків)
Верхня точка К
Аналогічно може бути геометрично вирішена гра з матрицею Стратегії, що відповідають Аналогічно можна геометрично розв’язати гру з матрицею Контрольні питання 1. Як визначаються нижня і верхня ціни гри? 2. Які стратегії гравців називаються максимінною і мінімаксною? 3. Що називається розв’язанням гри в змішаних стратегіях? 4. Як вирішити гру аналітично у випадку квадратної матриці другого порядку? 5. Як геометрично одержати розв’язок гри в змішаних стратегіях?
Лекція 12
1. Рівняння і нерівності моделі 2. Вибір заміни змінних, перехід до задачі лінійного програмування 3. Постановка двоїстої задачі 4. Приклад військово-тактичної гри
1. Постановка задачі. Два гравці:
Припустимо, що матриця не має сідловкої точки, значить
При правильній грі гарантійний виграш першого гравця:
Для другого гравця:
Ці нерівності доповнюються умовами:
2.Припустимо, що
Результат:
Треба ввести цільову функцію для одержання задачі лінійного програмування. Цільова функція:
Задачу можна розв’язати симплекс-методом. У результаті знайдемо вектор Одержуємо:
Для
де
Задача (12.8) – (12.10) є двоїстою для задачі (12.4) – (12.6) і Оптимальний план задачі:
Якщо умова
Значення гри вийде збільшеним на число
Після закінчення розв’язання знаходимо 4. Приклад військово-тактичної гри. Дві воюючі армії ведуть боротьбу за 2 пункти. Перша армія складається з 4-х полків, друга армія має 3 полки. Армія, що посилає більше полків на той чи інший населений пункт займає його і знищує всі спрямовані на цей пункт сили супротивника. Відповідний гравець одержує одиницю за зайнятий пункт і по одиниці за кожен знищений полк супротивника. У разі рівності сил, спрямованих у деякий пункт, очки не виграються. Мета гри: розподілити сили так, щоб одержати максимальний загальний виграш. Стратегія кожного гравця буде визначатися парою чисел
Матриця гри
Цільова функція:
Розв’язок
Не рекомендовані другий і четвертий варіанти. Для супротивника Контрольні питання 1. Скільки змінних містить загальна математична модель матричної гри? 2. Який вид задачі лінійного програмування? 3. Як знайти розв’язок задач лінійного програмування? 4. Як одержати розв’язок гри в змішаних стратегіях?
Лекція 13
1. Основні визначення в іграх із природою 2. Критерії при розв’язуванні ігор з природою 3. Приклад гри: планування будівництва електростанції
Раніше були розглянуті парні ігри, учасники яких мали протилежні інтереси. Тому дії кожного гравця (стратегії) мали на меті збільшення виграшу (зменшення програшу) при відомих варіантах поводження супротивника. У багатьох реальних задачах невизначеність викликається відсутністю інформації про дії супротивника і його можливих стратегій, такі ігри називаються іграми з природою. Приклад. Сільськогосподарське виробництво: вирощування зернових. Стратегія людини визначається термінами посіву, технологією проведення робіт, розподілом культур по площах, кількістю і термінами внесених добрив, застосуванням засобів захисту, зрошенням (де є можливість). Людина, в іграх із природою повинна діяти обачно, застосовуючи,наприклад, Природа діє випадково, її можливі стратегії визначаються як стани природи (умови погоди, ринковий попит на деяку продукцію, обсяг перевезень деяким видом транспорту). У деяких найпростіших задачах можливо заздалегідь визначити всі стани природи й імовірності появи цих станів. В інших задачах розподіл ймовірностей є невідомим.
Припустимо, що вдається на підставі попередніх розрахунків одержати матрицю:
Кожен елемент цієї матриці – виграш людини, у результаті застосування стратегій Крім цієї матриці, може використовуватися матриця ризиків
Ризик – різниця між виграшем, що могла б одержати людина, якби знала стан природи
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.3.204 (0.007 с.) |

 , матриця не містить сідловкої точки. Застосування мінімаксних стратегій забезпечить виграш не менше
, матриця не містить сідловкої точки. Застосування мінімаксних стратегій забезпечить виграш не менше  і програш не більше
і програш не більше  відповідно. У цьому випадку говорять про розв’язок гри в змішаних стратегіях: кожний із гравців буде застосовувати кілька стратегій при їхньому випадковому виборі.
відповідно. У цьому випадку говорять про розв’язок гри в змішаних стратегіях: кожний із гравців буде застосовувати кілька стратегій при їхньому випадковому виборі. ;
; 
 і
і  - це ймовірності, з якими кожен гравець застосовує свої первісні, чисті стратегії.
- це ймовірності, з якими кожен гравець застосовує свої первісні, чисті стратегії.


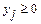

 змінними є
змінними є 
 - оптимальні ймовірності стратегій
- оптимальні ймовірності стратегій – значення гри чи ціна гри
– значення гри чи ціна гри
 .
. ;
; 
 .
. ;
; 





 :
:

 – нижня ціна гри
– нижня ціна гри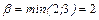 – верхня ціна гри
– верхня ціна гри . Шукаємо розв’язок гри в змішаних стратегіях.
. Шукаємо розв’язок гри в змішаних стратегіях.


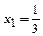


 . Аналогічно
. Аналогічно 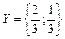 .
.


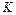
 називається нижньою межею виграшу.
називається нижньою межею виграшу.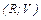 визначає розв’язок гри ціну значення гри та ймовірностей.
визначає розв’язок гри ціну значення гри та ймовірностей.
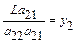

 . Результат розв’язання: ціна гри
. Результат розв’язання: ціна гри 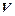 ; імовірності
; імовірності  й
й  і вектор
і вектор  називають активними стратегіями.
називають активними стратегіями. . Геометричний метод може бути використаний тільки для знаходження активних стратегій гравців. Для квадратної матриці другого порядку, що залишилася, розв’язок може бути знайдений аналітично.
. Геометричний метод може бути використаний тільки для знаходження активних стратегій гравців. Для квадратної матриці другого порядку, що залишилася, розв’язок може бути знайдений аналітично. і
і 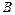 . Гра скінченна, маємо
. Гра скінченна, маємо  стратегій гравця
стратегій гравця  і n стратегій гравця
і n стратегій гравця  . Задано матрицю гри
. Задано матрицю гри  ,
,  ;
;  ; елементи якої є можливими виграшами гравця
; елементи якої є можливими виграшами гравця  . Гра розв’язується в змішаних стратегіях. Вектори ймовірностей
. Гра розв’язується в змішаних стратегіях. Вектори ймовірностей  і
і  .
.



 . Введемо нову змінну:
. Введемо нову змінну:




 і
і  .
.
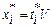 ,
, 

 ,
,
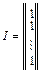 ;
; 
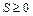
 .
.


 .
.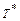 знаходиться тим же самим способом.
знаходиться тим же самим способом.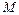 :
: .
. і
і  ;
;  .
. .
. – на II пункт.
– на II пункт.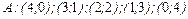 – стратегії першого гравця
– стратегії першого гравця  .
. – стратегії другого гравця
– стратегії другого гравця  .
.





 ;
; 
 .
. чи
чи  стратегію.
стратегію. - стратегії гравця
- стратегії гравця  - можливі стани природи;
- можливі стани природи;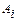 , якщо стан природи
, якщо стан природи  .
.
 .
.


