
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування задач на мінімум цільової функціїСодержание книги Поиск на нашем сайте
Розглянемо задачу: Z = C ∙ X " min AX ≤ B X ≥ 0
Позначимо F = - Z. Тоді max F= -min Z, і можна розв’язувати задачу (3.1)-(3.3) 3. Розглянемо пари симетричних задач. F = C ∙ X"max (3.1) Z = Y ∙ B " min (3.4) (3.4) A ∙ X ≤ B (3.2) Y∙A ≥ C (3.5) (3.5) X ≥ 0 (3.3) Y ≥ 0 (3.6) (3.6) де Кожна задача називається двоїстою стосовно іншої. Якщо вихідна задача (3.1)-(3.3) є задачею про оптимальний план випуску продукції, то двоїста (3.4)-(3.6) є задача про використання ресурсів. yi- ціна (оцінка) відповідного ресурсу, а Z=Y∙ В - вартість усіх ресурсів. Вихідна задача: скільки і якої продукції виробити, щоб при заданих обсягах ресурсів і цінах на продукцію забезпечити максимальний доход. Двоїста задача: якою повинна бути ціна кожного з ресурсів, щоб за даних обсягів ресурсів і цінах на продукцію забезпечити мінімум усіх витрат. Теорема. Якщо з пари двоїстих задач в одній є оптимальний план, то й інша має розв’язок, при цьому min Z=max F. Якщо цільова функція однієї з задач не обмежена, то й інша не має розв’язку. Теорема справедлива і для пари несиметричних задач: F = С ∙ X ® max Z = Y ∙ У ® min А ∙ X = В Y ∙ A ³ C X Умова невід’ємності для другої задачі відсутня. Уведенням додаткових змінних пара симетричних задач перетворюється на пару несиметричних. Розв’язуючи більш просту задачу, можна одержати одночасно і розв’язок двоїстої задачі.
4. Приклад Z = x1 + 2x2 + 3x3 ®min
Складемо і розв’яжемо двоїсту задачу. F = 2y1 + 3у2 + 6у3 + 3у4 ® max
Уводимо додаткові змінні.
F = 2y1 + 3у2 + 6у3 + 3у4 +0×у5+0×у6+0×у7® max
Одержали розв’язок двоїстої задачі.
Для вихідної задачі Zmin = 10,5.
Оптимальний план вихідної задачі знаходимо у рядку оцінок останньої таблиці в стовпцях векторів, що входили в первісний базис: хj = Fj. х1 = 1,5+0 = 1,5 х2 = 4,5+0 = 4,5 х3 = 0+0 = 0 Zmin = Z (X*) = 10,5 Контрольні запитання 1. Як перетворити неканонічну ЗЛП у канонічну за допомогою додаткових змінних? 2. Яким є алгоритм розв’язування задач ЛП на мінімум цільової функції? 3. Що таке симетричні задачі ЛП? 4. Як виявляється двоїстість при розв’язуванні пари несиметричних задач ЛП?
Лекція 4 Цілочисельне програмування
1.У багатьох реальних задачах на змінні величини накладаються додаткові умови: вони повинні бути цілими. Округлення результатів розв’язку, отриманого звичайним симплекс-методом може привести до результату, далекому від оптимального. Необхідний спеціальний метод, що враховує цілочисельність. Розглянемо найпростішу задачу:
Метод Гоморі 1. Вихідна задача вирішується симплекс-методом без умови (4.4); одержуємо деякий оптимальний план. 2. Якщо всі координати цього плану цілі – задача розв’язана. 3. Якщо ні – додаються додаткові обмеження. 4. Розширена задача розв’язується симплекс-методом і т.д.
Після розв’язування отримуємо оптимальний цілочисельний план або доводимо, що цілочисельного плану задача не має. Недоліки методу: вимога цілочисельності для всіх змінних задачі (як основних так і додаткових). Будемо вважати, що результатом пункту 1 розв’язування задачі (7.1)-(7.3) є такий план Припустимо, що xi - дробове число. Позначимо через [ xi ] його цілу частину, через qi=xi-[xi]={xi} - його дробову частину. Розглянемо рядок i останньої симплекс-таблиці
Якщо в цьому рядку дробових елементів не має, то задача (4.1)-(4.4) не має розв’язків. Припустимо, що xij – дробові, j=m+1,…n... Позначимо –qim+1∙ xm+1 - qim+2∙ xm+2-...-qinxn+qi≤ 0 (4.5) Додамо змінну xm+1 і перетворимо (4.5) у рівність: –qim+1xm+1-qim+2xm+2-…-qinxn+xn+1=-qi+1 Розв’яжемо отриману задачу двоїстим симплексом-методом. 3.Приклад
Приведемо задачу до канонічного вигляду і розв’яжемо симплекс-методом без умови цілочисельності змінних
Тому що х1 =1/3 і х2= 11/3 не цілі, необхідно доповнити задачу обмеженням. Будемо працювати з другим рядком q2 =2/3; -2/3x4-1/3x5-2/3x6+x7=-2/3
Одержали цілочисельний план
Залишаючи вихідні змінні, одержуємо Тому що 15<
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.242.160 (0.008 с.) |

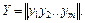
 0
0 xj ³ 0; j = 1,2,3.
xj ³ 0; j = 1,2,3. уi ³ 0; i = 1,2,3,4
уi ³ 0; i = 1,2,3,4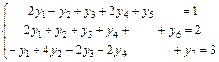
 План не є оптимальним F (Y0) = 0.
План не є оптимальним F (Y0) = 0. План не є оптимальним F (Y1) = 6.
План не є оптимальним F (Y1) = 6. План оптимальний F (Y2) = 10,5.
План оптимальний F (Y2) = 10,5. ; Fmax = F (Y*) = 10,5.
; Fmax = F (Y*) = 10,5.
 (4.1) (7.1)
(4.1) (7.1) i = 1, 2, 3...m (4.2)(7.2)
i = 1, 2, 3...m (4.2)(7.2) (4.3) (7.3)
(4.3) (7.3) цілі (4.4) (7.4)
цілі (4.4) (7.4)

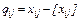 - дробові частини цих чисел. Уведемо додаткове обмеження
- дробові частини цих чисел. Уведемо додаткове обмеження
 xj>0, цілі, j=1,2,3.
xj>0, цілі, j=1,2,3.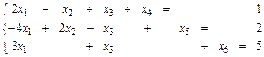

 1
1
 -3
-3

 1
1
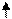 1
1


 3
3
 План не оптимальний
План не оптимальний План не оптимальний
План не оптимальний План не оптимальний
План не оптимальний План оптимальний
План оптимальний ; F* = 46/3
; F* = 46/3 q25 =1/3; q26 =2/3
q25 =1/3; q26 =2/3 - план умовно припустимий.
- план умовно припустимий.

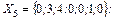 F(Х5)=15
F(Х5)=15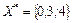 F(Х*)=15
F(Х*)=15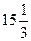 , точка максимуму з умовою цілочисельності координат знаходиться усередині припустимої множини.
, точка максимуму з умовою цілочисельності координат знаходиться усередині припустимої множини.


