
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимізаційні методи та моделіСодержание книги Поиск на нашем сайте ОПТИМІЗАЦІЙНІ МЕТОДИ ТА МОДЕЛІ Конспект лекцій
Сєвєродонецьк 2013р.
УДК Конспект лекцій з дисципліни «Оптимізаційні методи та моделі» для напряму підготовки: 6.030504 «Економіка підприємства»/ Укл. О.Л. Бродський – Сєвєродонецьк: Вид-во ТI - 2013. – 84 с. Розроблено на підставі робочої програми дисципліни «Оптимізаційні методи та моделі»
Вступ
Дисципліна «Оптимізаційні методи та моделі» є частиною більш об’ємного курсу «Економіко-математичне моделювання». Метою навчання є наукове кількісне обґрунтування рішень, що приймаються по управлінню в господарчих, фінансових, державних та інших справах. Інструментом, що застосовується для постановки та розв’язання відповідних задач є математичне моделювання, тобто створення математичних моделей виробничих, торгових, транспортних та інших процесів. Оптимізаційні моделі охоплюють випадки безпосереднього економічного формулювання мети розв’язання проблеми. Конспект містить 14 лекцій відповідно до діючого робочого плану спеціальності «Економіка підприємства». Розглянуті лінійні та нелінійні моделі різних рівнів та методи розв’язання задач оптимізації в умовах цих моделей.
Зміст 1. Вступ………………………………………………………………………..3 2. Лекція 1.Концептуальні аспекти математичного моделювання економіки.Оптимізаційні економіко-математичні моделі…….5 3.Лекція 2.Задачі лінійного програмування та методи їх розв’язування...8 4.Лекція 3.Розв’язування задачі лінійного програмування не в канонічній формі.Двоїстість у лінійному програмуванні………………16 5.Лекція 4. Цілочисельне програмування………………………………...21 6.Лекція 5.Транспортна задача. Побудова опорного плану……………..28 7. Лекція 6. Транспортна задача. Поліпшення плану. Розв’язування задачі у відкритій моделі…………………………………………… 34 8. Лекція 7. Моделі галузевого планування………………………………42 9. Лекція 8. Моделі управління запасами…………………………………46 10.Лекція 9. Багатопродуктові моделі управління запасами…………….53 11. Лекція 10. Ймовірносні моделі управління запасами. Основні поняття теорії ігор……………………………………………………59 12. Лекція 11. Матричні ігри………………………………………………..63 13.Лекція 12. Зведення матричної гри до задачі лінійного програмування. …………………………………………….69 14. Лекція 13. Ігри з природою…………………………………………….73 15. Лекція 14. Динамічні моделі…………………………………………...77
Лекція 1
1. Економіко-математичним моделювання Моделлю називається спеціально створений об'єкт, на якому відтворюються визначені характеристики досліджуваного об'єкта з метою дослідження його форми, співвідношень, властивостей. Метод, що включає в себе побудову моделі, називається моделюванням. За способом побудови розрізняють моделі: логічні, фізичні, математичні. Математичною моделлю називається опис об'єкта (процесу) рівняннями, нерівностями та іншими засобами математики. Економіко-математичним моделюванням називається теорія, методи та алгоритми розв’язання задач з економічним змістом у математичній формі. Потреба в такому моделюванні виникає в різних задачах економічного аналізу, планування, прогнозування та ін. Математичні методи одержання розв’язків для найпростіших задач об’єднані назвою математичне програмування.
2.Класифікація економіко-математичних моделей
Схема економіко-математичного моделювання: 1) постановка задачі; 2) побудова формалізованої схеми; 3) побудова моделі; 4) дослідження моделі; 5) оцінка отриманого рішення задачі. Загальна задача лінійного програмування (ЗЛТ)
Контрольні запитання 1. Що таке математична модель? 2. Як формулюється задача оптимального планування випуску продукції? 3. Який зміст є у параметрів та змінних цієї задачі? 4. Який вигляд має загальна ЗЛП? Лекція 2 Алгоритм симплекс-методу
Теорема. Якщо В>0, задача (2.4) - (2.6) завжди має розв’язок; він може бути отриманий за кінцеве число кроків.
3. Запишемо (2.5) в іншій формі:
x1 • A1 + x2 • A2 +...+ xn • An = B, (2.7) де
Припустимо, що матриця А містить у собі одиничну матрицю порядку m, розташовану в перших m стовпцях А1, А2,...АМ. Тоді початковий план Х0 має вигляд:
Перехід від одного плану до іншого здійснюється заміною одного вектора базису на інший, що раніше не входив у базис. Розв’язок (план) системи (2.5) за умови (2.6) назвемо припустимим. Ненульовий припустимий розв’язок задачі називається опорним розв’язком (планом), якщо вектори Аj, щовідповідають додатним координатам плану утворюють незалежну лінійну систему. Якщо число векторів у цій системі дорівнює m, план називається не виродженим, якщо менше - виродженим. План (вектор) X тоді і тільки тоді є опорним розв’язком задачі, коли точка Лекція 3 Не в канонічній формі Лекція 4 Цілочисельне програмування
1.У багатьох реальних задачах на змінні величини накладаються додаткові умови: вони повинні бути цілими. Округлення результатів розв’язку, отриманого звичайним симплекс-методом може привести до результату, далекому від оптимального. Необхідний спеціальний метод, що враховує цілочисельність. Розглянемо найпростішу задачу:
Метод Гоморі 1. Вихідна задача вирішується симплекс-методом без умови (4.4); одержуємо деякий оптимальний план. 2. Якщо всі координати цього плану цілі – задача розв’язана. 3. Якщо ні – додаються додаткові обмеження. 4. Розширена задача розв’язується симплекс-методом і т.д.
Після розв’язування отримуємо оптимальний цілочисельний план або доводимо, що цілочисельного плану задача не має. Недоліки методу: вимога цілочисельності для всіх змінних задачі (як основних так і додаткових). Будемо вважати, що результатом пункту 1 розв’язування задачі (7.1)-(7.3) є такий план Припустимо, що xi - дробове число. Позначимо через [ xi ] його цілу частину, через qi=xi-[xi]={xi} - його дробову частину. Розглянемо рядок i останньої симплекс-таблиці
Якщо в цьому рядку дробових елементів не має, то задача (4.1)-(4.4) не має розв’язків. Припустимо, що xij – дробові, j=m+1,…n... Позначимо –qim+1∙ xm+1 - qim+2∙ xm+2-...-qinxn+qi≤ 0 (4.5) Додамо змінну xm+1 і перетворимо (4.5) у рівність: –qim+1xm+1-qim+2xm+2-…-qinxn+xn+1=-qi+1 Розв’яжемо отриману задачу двоїстим симплексом-методом. 3.Приклад
Приведемо задачу до канонічного вигляду і розв’яжемо симплекс-методом без умови цілочисельності змінних
Тому що х1 =1/3 і х2= 11/3 не цілі, необхідно доповнити задачу обмеженням. Будемо працювати з другим рядком q2 =2/3; -2/3x4-1/3x5-2/3x6+x7=-2/3
Одержали цілочисельний план
Залишаючи вихідні змінні, одержуємо Тому що 15< Приклад. Виділено 20 тисяч гривень на придбання устаткування для нової ділянки, Уведемо змінні
Обмеження:
Розв’язання:
Складемо початковий план
План оптимальний: Метод Гоморі: Обмеження: Новий план
Рекомендується придбання 2 машин типу
Контрольні запитання 1. Якою є постановка задачі цілочисельного програмування? 2. Яким є алгоритм методу Гоморі для ЗЦП? 3. Які недоліки методу Гоморі? Лекція 5 Транспортна задача Побудова опорного плану
1. Маємо деякий продукт (товар), що знаходиться в декількох постачальників (виробників), відомі обсяги цього продукту. Маються замовники (споживачі) товару з відомими обсягами потреб. Відомі питомі витрати по доставці товару від будь-якого можливого постачальника до будь-якого можливого споживача. Потрібно скласти план розподілу товару, щоб усі потреби були задоволені, весь товар вивезений і загальна вартість (загальні витрати) була мінімальною.
2. Уведемо наступні позначення:
Позначимо через Тоді загальні витрати за всіма маршрутами
Одержали наступну лінійну модель цільова функція
Економічний зміст обмежень: (5.2) – весь товар постачальників вивезений (5.3) – усі потреби споживачів задоволені (5.4) – товар за кожним маршрутом або планується до перевезення (хij >0) або не планується (хij = 0). Задача є лінійною, загальне число змінних Для викладення методів додамо умову:
Зміст умови (5.5); загальний обсяг запасів товару дорівнює загальному обсягу потреб. Модель (5.1)-(5.4) з додатковою умовою (5.5) називається закритою, без неї – відкритою. Теорема. Будь-яка закрита модель транспортної задачі має розв’язок.
3. Побудова початкового опорного плану для закритої моделі Будемо заповнювати таблицю з m рядками і n стовпчиками. Клітину таблиці назвемо зайнятою, якщо в неї поміщене перевезення xij>0. Інші клітини називаються вільними, xij = 0 у них не ставляться. У системі рівнянь (5.2), (5.3) і (5.5) усього m+n-1 незалежних рівнянь, тому опорний план задачі повинен містити не більш m+n-1 зайнятих клітин. Якщо N = m+n-1 - план називається не виродженим, якщо N<m+n-1 – виродженим. Циклом у заповненій таблиці називається замкнута ламана лінія з вершинами в зайнятих клітинах.
Приклади циклів: Опорний план не повинен містити циклів.
4. Розглянемо кілька методів побудови опорного плану транспортної задачі. Метод подвійної переваги. 1. У кожному рядку знаходиться клітина з найменшою ціною і позначається позначкою. 2. Те ж саме проводиться для кожного стовпчика. 3. Заповнення таблиці починаємо з клітин, відзначених двома позначками. 4. Після цього заповнюються клітини з однією позначкою. 5. У таблиці, що залишилася, застосовується метод мінімальної вартості.
Схема плану: N=7 План опорний, вироджений Z=4250 (гр. од.) З трьох викладених методів даний метод, як правило, дає план з меншою загальною вартістю порівняно з іншими методами.
Контрольні запитання 1. Як економічно формулюється транспортна задача? 2. Якою є математична модель ТЗ? 3. Як треба будувати первісний план ТЗ за методом північно-західного кута? 4. Що таке цикл у таблиці ТЗ? 5. Якими є алгоритми методів найменшої вартості та подвійної переваги?
Лекція 6 Транспортна задача Поліпшення плану Розв’язування задачі у відкритій моделі
1. Загальний алгоритм розв’язування ТЗ 2. Перетворення виродженого плану у не вироджений 3. Метод потенціалів для оцінки плану 4. Поліпшення плану в циклі перерозподілу постачань. Приклад розв’язування ТЗ 5. Розв’язування ТЗ у відкритій моделі
1. Загальний алгоритм розв’язування транспортної задачі: а)Побудова початкового опорного плану. б)Оцінка плану на оптимальність. в)Поліпшення плану, якщо він не є оптимальним. г)Оцінка плану і т.д. 2. Для поліпшення плану необхідно провести його оцінку. Якщо є не вироджений опорний план, його можна оцінювати. Вироджений план необхідно зробити не виродженим. Для цього необхідно доповнити план клітиною з перевезенням, яке дорівнює нулю. Це не змінить розподіл товару, але збільшить на одиницю число зайнятих клітин. Вибір клітини, що доповнює план, варто зробити так, щоб не з'явився цикл (без втрати опірності). 3. Кожній зайнятій клітині ставиться у відповідність два числа – потенціали постачальника і споживача. При цьому їхня сума прирівнюється ціні, що міститься в цій клітині. ui-потенціал постачальника; vj-потенціал споживача. ui+ vj = cij (6.1) У цій системі невідомих m+n, число рівнянь m+n-1. Отже, система має безліч розв’язків. Досить одержати один розв’язок системи. Для цього можна припустити, що u1=0 і знайти інші невідомі з відповідних рівнянь. Для кожної вільної клітини (i; j) обчислюється сума потенціалів постачальника і споживача dij=ui+vj і записується в цю клітину. Якщо для всіх вільних клітин виконана нерівність dij ≤ cij (6.2) план перевезень оптимальний. Якщо для деякої клітини dij >cij (6.3) план не є оптимальним і його можна поліпшити. 4. Поліпшення плану досягається перерозподілом постачань за циклом. Цикл повинен містити вершину в клітині з умовою (6.3), а інші вершини – у зайнятих клітинах. Обсяг товару, що перерозподіляється, дорівнює мінімумові з обсягів перевезень, що складаються в клітинах з парними номерами за циклом, початок якого знаходиться в обраній клітині з порушенням (6.2). (Інше пояснення буде в прикладі). Розглянемо викладене на прикладі. Наступний початковий план отриманий методом мінімальної вартості.
Z= 1005 гр.од. Схема плану:
План опорний. Кількість зайнятих клітин N=7, план не вироджений.
Складемо систему рівнянь для потенціалів
u1 + v4 = 4 u4 + v2 = 3 u2 + v1 = 1 u4 + v4 = 7 u3 + v4 = 2 u2 + v4 = 9
Нехай u1 = 0; тоді одержимо v3 = 3; v4 = 4; u2 = 5; v1 = -4; u4 = 3; v2 = 0; u3 = 2 Знайдемо суми потенціалів для вільних клітин і порівняємо з відповідними цінами
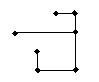
План не оптимальний, тому що в клітині (2,3) 8 > 6 і в клітині (3,4) 6 > 4. Виберемо клітину (3,4) і побудуємо цикл перерозподілу.
min (40, 45) = 40. Передача від «-» до «+» 40 од. товару Одержали новий план перевезень; обчислимо його вартість, побудуємо схему плану і розрахуємо потенціали.
Вартість плану
Схема плану: План опорний, не вироджений і не оптимальний; у клітині (2,3) 8 > 6. Побудуємо цикл перерозподілу 90 10 80 20
min (90, 10) = 10 – кількість одиниць товару, перерозподілена за циклом. Новий план перевезень
Вартість плану Z= 905 гр.од. План оптимальний, тому що для всіх вільних кліток виконана умова (6.3). Загальна постановки задачі Мається деякий склад для збереження
У моделі без дефіциту витрати двох видів: 1. витрати за замовленням і доставкою товарів; 2. витрати збереження; Задача має тривіальне рішення.
Недоліки цього рішення: 1. склад працює як перевалочна база; 2. неможливість реалізації рішення на практиці: а) для багатьох видів товарів існують мінімальні обсяги партій; б) загальний обсяг може бути занадто великий для одночасної доставки (транспортне обмеження). Висновок: для реального працюючого складу (оптової бази) практично неможливе одноразове завезення за всією номенклатурою товарів. Формулювання однієї з конкретних задач – визначити графік доставки товарів у такій черговості й у такій кількості, щоб при безумовному задоволенні попиту середньої обсяг (рівень) запасів був мінімальним. Математичні методи розв’язання подібних задач створюють теорію управління запасами.
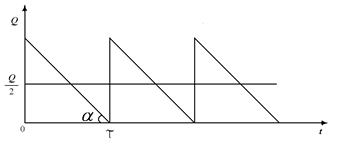
Однопродуктова модель Уїлсона: 1. на складі зберігається один товар (продукт); 2. попит на товар є постійним (рівень запасу товару зменшується з постійною швидкістю) 3. у той момент, коли запас вичерпаний, подається заявка на доставку нової партії товарів; 4. виконання заявки (замовлення) здійснюється миттєво; 5. накладні витрати, пов'язані з замовленням і доставкою товару постійні і не залежать 6. щоденна вартість збереження одиниці товару Схема роботи складу
3.Плануємо роботу складу на деякий період Т Розраховуємо кількість замовлень: Загальні витрати за замовленням і доставкою:
Середній рівень запасу: Витрати на збереження в одному періоді: Загальні витрати на збереження: Загальні витрати в плановому періоді S:
Знайдемо мінімум складеної функції витрат.
Можна перевірити, що Q * - це точка мінімуму:
Висновок: у точці мінімуму витрати збереження дорівнюють витратам на замовлення і доставку.
Знайдемо інтервал між замовленнями.
Практичні труднощі при використанні моделі Уїлсона: 1. теоретична оптимальна величина
2. оптимальне
Напрямки ускладнення моделі Уїлсона: 1. Модель з дефіцитом. 2. 3. Моделі з випадковим попитом 4. Багатопродуктові моделі. Моделі з випадковим попитом Існує однопродуктовий склад. Вважаємо, що попит | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

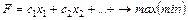
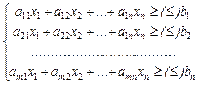
 ; j= 1 ,... n
; j= 1 ,... n

 ;
;  ;....
;....  - стовпці матриці А.
- стовпці матриці А. або у вигляді вектора
або у вигляді вектора  . (2.8)
. (2.8) (4.1) (7.1)
(4.1) (7.1) i = 1, 2, 3...m (4.2)(7.2)
i = 1, 2, 3...m (4.2)(7.2) (4.3) (7.3)
(4.3) (7.3) цілі (4.4) (7.4)
цілі (4.4) (7.4)

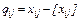 - дробові частини цих чисел. Уведемо додаткове обмеження
- дробові частини цих чисел. Уведемо додаткове обмеження
 xj>0, цілі, j=1,2,3.
xj>0, цілі, j=1,2,3.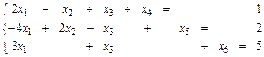

 1
1
 -3
-3

 1
1
 1
1


 3
3
 План не оптимальний
План не оптимальний План не оптимальний
План не оптимальний План не оптимальний
План не оптимальний План оптимальний
План оптимальний ; F* = 46/3
; F* = 46/3 q25 =1/3; q26 =2/3
q25 =1/3; q26 =2/3 - план умовно припустимий.
- план умовно припустимий.

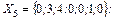 F(Х5)=15
F(Х5)=15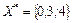 F(Х*)=15
F(Х*)=15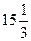 , точка максимуму з умовою цілочисельності координат знаходиться усередині припустимої множини.
, точка максимуму з умовою цілочисельності координат знаходиться усередині припустимої множини. м2. Розглядається два види устаткування. Машина типу
м2. Розглядається два види устаткування. Машина типу 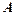 коштує 5 тис. грн., займає 8м2 і має продуктивність 7 тис.од. продукції за зміну. Машина типу
коштує 5 тис. грн., займає 8м2 і має продуктивність 7 тис.од. продукції за зміну. Машина типу  коштує 2 тис. грн., займає 4м2, і забезпечує виробництво 3 тис. од. продукції за зміну. Розрахувати оптимальний план придбання устаткування, що забезпечить за даних обмежень максимальну продуктивність ділянки.
коштує 2 тис. грн., займає 4м2, і забезпечує виробництво 3 тис. од. продукції за зміну. Розрахувати оптимальний план придбання устаткування, що забезпечить за даних обмежень максимальну продуктивність ділянки.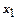 і
і  – плановану кількість машин. Складемо цільову функцію.
– плановану кількість машин. Складемо цільову функцію.

 , цілі
, цілі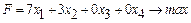





 , але
, але  – неціле.
– неціле. .
.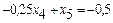 .
.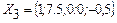 майже припустимий, застосовується двоїстий симплекс-метод. Одержуємо рішення:
майже припустимий, застосовується двоїстий симплекс-метод. Одержуємо рішення: – план оптимальний.
– план оптимальний. =29
=29 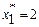
 .
. м2 площі приміщення.
м2 площі приміщення.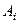 - постачальники,
- постачальники,  - обсяг (кількість) товару в кожного з них;
- обсяг (кількість) товару в кожного з них;  .
. - споживачі,
- споживачі,  - обсяг потреб кожного з них;
- обсяг потреб кожного з них; 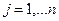 .
. - матриця цін (питомих витрат), де
- матриця цін (питомих витрат), де  - ціна перевезення товару за маршрутом від
- ціна перевезення товару за маршрутом від 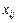 - кількість продукту (обсяг перевезень) за маршрутом від
- кількість продукту (обсяг перевезень) за маршрутом від 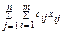
 (5.1)
(5.1) i = 1, 2,...m (5.2)
i = 1, 2,...m (5.2) j = 1, 2,...n (5.3)
j = 1, 2,...n (5.3) (5.4)
(5.4) . Задача може бути розв’язана симплекс-методом; крім цього для неї розроблені спеціальні методи розв’язування.
. Задача може бути розв’язана симплекс-методом; крім цього для неї розроблені спеціальні методи розв’язування.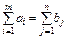 (5.5)
(5.5)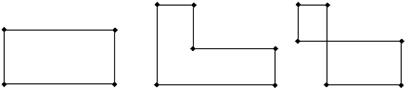

 Вартість плану
Вартість плану u1 + v3 = 3 u3 + v2 = 2
u1 + v3 = 3 u3 + v2 = 2 75 * 35 40
75 * 35 40





 45 40 85
45 40 85 Z= 925 гр.од. N = 7.
Z= 925 гр.од. N = 7.

 * 10 10
* 10 10 найменувань товарів. Відомий щоденний попит на кожен вид товарів
найменувань товарів. Відомий щоденний попит на кожен вид товарів  Відома загальна ємність (місткість) складу
Відома загальна ємність (місткість) складу  . Потрібно визначити процедуру завезення товарів на склад, при якій попит задовольняється і витрати мінімальні. Нехай
. Потрібно визначити процедуру завезення товарів на склад, при якій попит задовольняється і витрати мінімальні. Нехай  – обсяги партій відповідних товарів. Їхню суму позначимо через
– обсяги партій відповідних товарів. Їхню суму позначимо через  ,
, 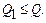
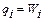
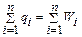
 ;
; від кількості товарів (обсягу партій)
від кількості товарів (обсягу партій)  ;
;
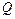 – максимальна кількість товару на складі;
– максимальна кількість товару на складі; 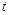 – час;
– час;  – інтервал часу між точками замовлення.
– інтервал часу між точками замовлення. ;
; 
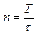 .
.

 .
.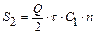
 ,
,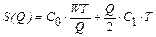
 ;
;  ;
; 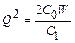 .
.






 не завжди може бути реалізована на практиці. Округлення
не завжди може бути реалізована на практиці. Округлення 
 також може бути практично не реалізованим.
також може бути практично не реалізованим. – змінний детермінований попит.
– змінний детермінований попит.


