
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обмеження за загальною вартістю запасуСодержание книги Поиск на нашем сайте
Додатково уведемо вектор
де Обмеження має вигляд: Складається функція Лагранжа (зручно повернутися до колишніх позначень).
Одержуємо наступний розв’язок.
Розміри партій зменшуються, витрати збільшуються
Обмеження витрат на здійснення замовлень
де Y – загальна вартість накладних витрат, пов'язаних з розміщенням замовлень на
Мінімальні витрати:
Порівняно з моделлю без обмеження, обсяги партій збільшуються, витрати також збільшуються.
Модель зі спільними замовленнями Вважаємо, що можна робити спільне замовлення на кілька товарів, що дозволяє зменшити загальні витрати. Для індивідуальних замовлень були отримані наступні формули:
Припустимо, що на всі товари можливе спільне замовлення з константою Число замовлень Загальні витрати замовлень: Загальні витрати:
Точка мінімуму:
Мінімальні витрати при спільному замовленні:
Порівнюючи витрати при різних системах замовлення, можна вибирати так звану політику (стратегію) замовлень.
Якщо а<1, вигідні спільні замовлення, для Розглянута нелінійна детермінована багатопродуктова модель управління запасами.
Контрольні питання 1. Яка загальна постановка задачі управління запасами для багатопродуктового складу? 2. Як знаходиться оптимальний розв’язок в задачі без обмежень? 3. Який загальний метод розв’язання задач з обмеженнями? 4. Як знаходяться оптимальні розв’язки в конкретних задачах з обмеженням? 5. Як впливають обмеження на обсяги партій товарів і оптимальні витрати? 6. Як розв’язується задача з дозволеними спільними замовленнями?
Лекція 10 1. Ймовірнісні моделі управління запасами: основні поняття 2. Розрахунок резервного запасу для ймовірнісної моделі 3. Основні поняття теорії ігор 4. Матриця гри
Моделі з випадковим попитом Існує однопродуктовий склад. Вважаємо, що попит
Припустимо, що Якщо подавати заявку в той момент, коли на складі залишилося Аналогічна ситуація, якщо Щоб зменшити ймовірність дефіциту, необхідне створення резервного запасу, тобто замовлення подається тоді, коли наявний запас товарів більше середньої потреби за середній час доставки.
2. Будемо вважати, що ця величина має нормальний розподіл; (
Для зручності розрахунку проведемо нормування випадкової величини
Щільність для цієї випадкової величини задається формулою:
R(К) – знаходиться за таблицею з умови
Обсяг партії товару розраховується за формулою Уїлсона.
Витрати збільшаться.
Якщо відмовитися від вимоги бездефіцитності, потрібно вводити штрафи за непостачання товарів. Основні поняття теорії ігор Теорією ігор називається теорія математичних моделей, у якій враховуються різні інтереси учасників. Зіткнення протилежних інтересів приводить до виникнення конфліктних ситуацій. Спрощена модель конфліктної ситуації називається грою. Конфлікт розвивається за певними правилами (правила гри). Природною базою теорії ігор є конкретні ігри: шашки, шахи, карткові ігри. Використовується термінологія: гравці (сторони конфлікту), виграш (результат конфлікту). Невизначеність результату гри викликається різними причинами: 1. Розмаїтість варіантів (шахи). 2. Вплив випадкових факторів. Якщо результат гри є невизначеним винятково через випадкові фактори, такі ігри називаються азартними. 3. Відсутність інформації стосовно дій супротивника і його планів – стратегічні ігри. Розглянемо більш докладно стратегічні ігри. Якщо учасників двоє, то гра називається парною, якщо більше двох – множинною. Зміст гри: послідовність дій, за чітко сформульованими правилами. Ці дії прийнято називати ходами. Правила гри – можливі варіанти дії гравців, інформація однієї сторони про дії іншої, результат гри після виконання послідовності ходів. Хід гравця – вибір одного з дозволених правил дій і його здійснення. Послідовність ходів буде називатися стратегією. Оптимальною стратегією називається така стратегія, яка при багаторазовому повторенні гри, забезпечує гравцю максимально можливий середній виграш. Припустимо, що інтереси учасників гри описується кількісно, тобто результатом гри є число (виграш). 4. Найпростішим видом стратегічної гри є парна скінченна гра з нульовою сумою. Гра складається з двох ходів: гравець Задаються дві функції:
Залишимо одну функцію Мета гри: для гравця А - одержати max φ, а для гравця В – одержати min φ.
Приклад.
Контрольні питання 1. Які випадкові величини присутні у ймовірнісних моделях управління запасами? 2. Яка мета резервного запасу? Як розрахувати цей запас? 3. Що називається грою? Що таке хід, стратегія, виграші? 4. Що таке матриця гри для скінченної парної гри з нульовою сумою? Лекція 11
1. Розв’язання матричної гри 2. Ігри в змішаних стратегіях 3. Розв’язання гри в змішаних стратегіях для квадратної матриці другого порядку 4. Графічний метод розв’язання гри. Рішення матричної гри 1.Розглянемо скінченну парну гру двох гравців
Передбачаючи таку можливість, гравець
Така стратегія
Стратегія Фактично виграш гравця Якщо
Це значення гри, а сама гра називається цілком визначеною. Для матриці це число називається сідловкою точкою.
Якщо один із гравців дотримується своєї оптимальної стратегії, то для іншого гравця відхилення від його оптимальної стратегії не може бути вигідним. Розглянемо приклад конкретної матриці, для якої знайдемо значення гри та оптимальні стратегії гравців.
Приклад.
Знайдемо нижню ціну гри:
Знайдемо верхню ціну гри:
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.140 (0.007 с.) |

 - ціни товарів і підрахуємо максимальну вартість усіх товарів на складі.
- ціни товарів і підрахуємо максимальну вартість усіх товарів на складі.

 ,
, поправочний коефіцієнт (нормувальний множник), враховує нерівномірність постачань товарів.
поправочний коефіцієнт (нормувальний множник), враховує нерівномірність постачань товарів. чи
чи  .
.

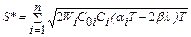
 − відношення двох видів витрат.
− відношення двох видів витрат. 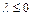
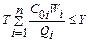 ,
,
 товарів і їхньою доставкою для одного планового періоду.
товарів і їхньою доставкою для одного планового періоду.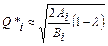
 ;
; 

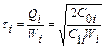 ,
, 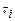 - інтервали між замовленнями.
- інтервали між замовленнями.
 . Нас цікавить
. Нас цікавить  – інтервал між замовленнями.
– інтервал між замовленнями. .
. .
.



 ; чи
; чи 
 – індивідуальні.
– індивідуальні. випадковий і доставка відбувається протягом деякого часу;
випадковий і доставка відбувається протягом деякого часу;  тривалість доставки. У момент
тривалість доставки. У момент  – повинно бути подане замовлення, щоб до моменту вичерпання запасу замовлення було доставлено.
– повинно бути подане замовлення, щоб до моменту вичерпання запасу замовлення було доставлено.

 – випадкова величина, для якої відоме середнє значення
– випадкова величина, для якої відоме середнє значення  , тоді
, тоді  .
.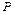 одиниць товару, то в 50% випадків до моменту доставки товарів запас буде вичерпаний.
одиниць товару, то в 50% випадків до моменту доставки товарів запас буде вичерпаний. є випадковою величиною з деяким середнім значенням
є випадковою величиною з деяким середнім значенням 
 - випадкова величина, це потреба в товарі за час його доставки.
- випадкова величина, це потреба в товарі за час його доставки. ) – параметри нормального закону. Вводимо в розгляд коефіцієнт ризику К и позначимо через
) – параметри нормального закону. Вводимо в розгляд коефіцієнт ризику К и позначимо через  – резервний, страховий запас.
– резервний, страховий запас. – кількість товару, що повинен бути на складі на момент замовлення.
– кількість товару, що повинен бути на складі на момент замовлення.

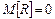




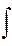



 . Після цього величину резервного запасу можна знайти за наступною формулою:
. Після цього величину резервного запасу можна знайти за наступною формулою:


 вибирає одну зі своїх можливих стратегій
вибирає одну зі своїх можливих стратегій  ,
, 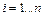 , гравець
, гравець  вибирає одну зі своїх можливих стратегій
вибирає одну зі своїх можливих стратегій  ,
,  ; при повному незнанні вибору іншого гравця.
; при повному незнанні вибору іншого гравця. – виграш гравця А.
– виграш гравця А. – виграш гравця В.
– виграш гравця В.
 .
. .
.
 ;
;  ;
; 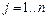 .
.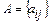 - матриця гри чи платіжна матриця.
- матриця гри чи платіжна матриця. Гравець А грає "рядками", а гравець У – "стовпцями".
Гравець А грає "рядками", а гравець У – "стовпцями". Задана функція
Задана функція  ,
,  .
. − матриця гри (платіжна матриця). Припустимо, що гравець
− матриця гри (платіжна матриця). Припустимо, що гравець  вибрав стратегію
вибрав стратегію 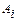 , тоді в найгіршому варіанті гри його виграш складе мінімум
, тоді в найгіршому варіанті гри його виграш складе мінімум  .
.
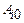 , що забезпечує величину виграшу
, що забезпечує величину виграшу  називається максимінною, число
називається максимінною, число  називається нижньою ціною гри. Якщо гравець
називається нижньою ціною гри. Якщо гравець 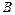 зробив вибір
зробив вибір 

 , по якій досягається ця величина, називається мінімаксною, а число
, по якій досягається ця величина, називається мінімаксною, а число  називається верхньою ціною гри.
називається верхньою ціною гри. ).
). , то це спільне значення позначається буквою
, то це спільне значення позначається буквою  .
. 



 гарантований виграш
гарантований виграш 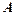 при правильній грі складає 2 од.
при правильній грі складає 2 од. гарантований програш гравця
гарантований програш гравця 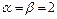 ; гра цілком визначена,
; гра цілком визначена,  – сідловка точка; оптимальні стратегії –
– сідловка точка; оптимальні стратегії – 



