Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача придбання устаткуванняСодержание книги Поиск на нашем сайте
Постановка задачі. Потрібно придбати виробниче устаткування (верстати, машини). Вибір робиться з Задано вектор ресурсів Потрібно скласти план придбання устаткування, щоб в умовах наявних ресурсів забезпечити максимальну продуктивність цеху (ділянки, відділення). Уведемо змінні
Обмеження:
Умова невід’ємності:
Додаткова умова:
Це лінійна задача цілочисельного програмування, розв’язується за допомогою методу Гоморі. Приклад. Виділено 20 тисяч гривень на придбання устаткування для нової ділянки, Уведемо змінні
Обмеження:
Розв’язання:
Складемо початковий план
План оптимальний: Метод Гоморі: Обмеження: Новий план
Рекомендується придбання 2 машин типу
Контрольні запитання 1. Якою є постановка задачі цілочисельного програмування? 2. Яким є алгоритм методу Гоморі для ЗЦП? 3. Які недоліки методу Гоморі? Лекція 5 Транспортна задача Побудова опорного плану
1. Маємо деякий продукт (товар), що знаходиться в декількох постачальників (виробників), відомі обсяги цього продукту. Маються замовники (споживачі) товару з відомими обсягами потреб. Відомі питомі витрати по доставці товару від будь-якого можливого постачальника до будь-якого можливого споживача. Потрібно скласти план розподілу товару, щоб усі потреби були задоволені, весь товар вивезений і загальна вартість (загальні витрати) була мінімальною.
2. Уведемо наступні позначення:
Позначимо через Тоді загальні витрати за всіма маршрутами
Одержали наступну лінійну модель цільова функція
Економічний зміст обмежень: (5.2) – весь товар постачальників вивезений (5.3) – усі потреби споживачів задоволені (5.4) – товар за кожним маршрутом або планується до перевезення (хij >0) або не планується (хij = 0). Задача є лінійною, загальне число змінних Для викладення методів додамо умову:
Зміст умови (5.5); загальний обсяг запасів товару дорівнює загальному обсягу потреб. Модель (5.1)-(5.4) з додатковою умовою (5.5) називається закритою, без неї – відкритою. Теорема. Будь-яка закрита модель транспортної задачі має розв’язок.
3. Побудова початкового опорного плану для закритої моделі Будемо заповнювати таблицю з m рядками і n стовпчиками. Клітину таблиці назвемо зайнятою, якщо в неї поміщене перевезення xij>0. Інші клітини називаються вільними, xij = 0 у них не ставляться. У системі рівнянь (5.2), (5.3) і (5.5) усього m+n-1 незалежних рівнянь, тому опорний план задачі повинен містити не більш m+n-1 зайнятих клітин. Якщо N = m+n-1 - план називається не виродженим, якщо N<m+n-1 – виродженим. Циклом у заповненій таблиці називається замкнута ламана лінія з вершинами в зайнятих клітинах.
Приклади циклів: Опорний план не повинен містити циклів.
4. Розглянемо кілька методів побудови опорного плану транспортної задачі.
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.247.170 (0.008 с.) |

 видів устаткування, для яких відома продуктивність
видів устаткування, для яких відома продуктивність 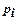 , а також деякі параметри (ціна, займана площа, кількість персоналу, що обслуговує, тощо). Усього
, а також деякі параметри (ціна, займана площа, кількість персоналу, що обслуговує, тощо). Усього  параметрів, задана матриця
параметрів, задана матриця  їхніх значень.
їхніх значень. (гроші, загальна площа, чисельність працівників і т.п).
(гроші, загальна площа, чисельність працівників і т.п).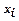 - кількість одиниць відповідного виду устаткування. Складемо модель.
- кількість одиниць відповідного виду устаткування. Складемо модель.

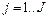

 - цілі
- цілі
 м2. Розглядається два види устаткування. Машина типу
м2. Розглядається два види устаткування. Машина типу 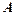 коштує 5 тис. грн., займає 8м2 і має продуктивність 7 тис.од. продукції за зміну. Машина типу
коштує 5 тис. грн., займає 8м2 і має продуктивність 7 тис.од. продукції за зміну. Машина типу  коштує 2 тис. грн., займає 4м2, і забезпечує виробництво 3 тис. од. продукції за зміну. Розрахувати оптимальний план придбання устаткування, що забезпечить за даних обмежень максимальну продуктивність ділянки.
коштує 2 тис. грн., займає 4м2, і забезпечує виробництво 3 тис. од. продукції за зміну. Розрахувати оптимальний план придбання устаткування, що забезпечить за даних обмежень максимальну продуктивність ділянки.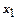 і
і  – плановану кількість машин. Складемо цільову функцію.
– плановану кількість машин. Складемо цільову функцію.

 , цілі
, цілі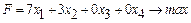





 , але
, але  – неціле.
– неціле. .
.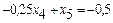 .
.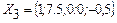 майже припустимий, застосовується двоїстий симплекс-метод. Одержуємо рішення:
майже припустимий, застосовується двоїстий симплекс-метод. Одержуємо рішення: – план оптимальний.
– план оптимальний. =29
=29 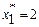
 .
. м2 площі приміщення.
м2 площі приміщення. - постачальники,
- постачальники,  - обсяг (кількість) товару в кожного з них;
- обсяг (кількість) товару в кожного з них;  .
. - споживачі,
- споживачі,  - обсяг потреб кожного з них;
- обсяг потреб кожного з них;  .
. - матриця цін (питомих витрат), де
- матриця цін (питомих витрат), де  - ціна перевезення товару за маршрутом від
- ціна перевезення товару за маршрутом від 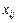 - кількість продукту (обсяг перевезень) за маршрутом від
- кількість продукту (обсяг перевезень) за маршрутом від 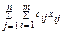
 (5.1)
(5.1) i = 1, 2,...m (5.2)
i = 1, 2,...m (5.2) j = 1, 2,...n (5.3)
j = 1, 2,...n (5.3) (5.4)
(5.4) . Задача може бути розв’язана симплекс-методом; крім цього для неї розроблені спеціальні методи розв’язування.
. Задача може бути розв’язана симплекс-методом; крім цього для неї розроблені спеціальні методи розв’язування.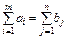 (5.5)
(5.5)