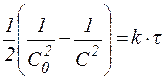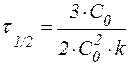Порядок и молекулярность реакции

Реакции, подчиняющиеся уравнениям типа:

принято классифицировать по признаку кинетического порядка.

Общим или суммарным порядком реакции называют сумму всех показателей степеней при концентрациях в выражении закона действующих масс, установленным опытным путем:

n = a + b + c …,

где a, b, с - частные порядки реакции, соответственно по веществам A, B и C.

Наиболее просты следующие случаи:

1) реакции нулевого порядка: , n = 0;

2) реакции первого порядка: , n = 1;

n = 2;

3) реакции второго порядка: ,

 

n = 3.

4) реакции третьего порядка: ,

,

С общим кинетическим порядком выше третьего встречаться практически не приходится.

Для элементарных реакций (т. е. протекающих в один элементарный акт) показатели степеней a, b и c обычно представляют собой положительные целые числа. Для более сложных реакций известны дробные и даже отрицательные показатели.

Другой характеристикой механизма протекания химических реакций является молекулярность реакции.

Молекулярностью реакции называется число молекул, участвующих в одном элементарном акте реакции.

Следует отметить, что понятие молекулярности можно применять только для элементарных реакций. К числу элементарных реакций относится, например, разложение 1,2-диметилдиазена:

CH₃N = NCH₃ C₂H₆ + N₂.

Данная реакция является мономолекулярной - в элементарном акте участвует одна молекула. Если в одном акте в реакцию вступают две молекулы, то реакция является бимолекулярной. Например:

H₂ + I₂ 2HI.

Соответственно при тримолекулярной реакции в одном элементарном акте участвуют три частицы (молекулы):

2NO + O₂ 2NO₂

Интересно, что большинство реакций, встречающихся на практике, кажутся простыми. Однако детальное изучение кинетики показывает, что зачастую они протекают по более сложным механизмам. Так, реакция термического разложения паров дихлорэтана:

CH₂Cl – CH₂Cl CHCl = CH₂ + HCl

на первый взгляд представляется элементарной.

 

Действительно, кинетическое уравнение этой реакции имеет вид:

,

что указывает на первый порядок.

Однако данная реакция не является мономолекулярной, так как протекает в несколько стадий:

1) C₂H₄Cl₂ C₂H₄Cl + Cl•

2) Cl• + C₂H₄Cl₂ C₂H₃Cl₂ + HCl

3) C₂H₃Cl₂ C₂H₃Cl + Cl•

4) C₂H₄Cl + Cl• C₂H₄Cl₂

В этом механизме первая и третья стадии мономолекулярны, а вторая и четвертая – бимолекулярны. Очевидно, говорить о молекулярности реакции разложения дихлорэтана в целом нельзя. В то же время можно говорить о ее первом кинетическом порядке.

Данный пример наглядно иллюстрирует факт, что порядок реакции далеко не всегда совпадает с ее молекулярностью. В целом, моно-, би- и тримолекулярные реакции являются, соответственно, реакциями первого, второго и третьего порядков; обратное же заключение может оказаться ошибочным.

Реакции I порядка

Для реакций I порядка убыль концентрации реагента определяется уравнением:

(8)

где С – концентрация вещества в данный момент времени;

С₀ – начальная концентрация вещества;

k_I – константа скорости реакции первого порядка;

t – время.

В логарифмической форме это выражение выглядит так:

(9)

 

Из приведенных формул можно сделать ряд важных заключений:

1) константа скорости реакции первого порядка имеет размерность [время^-1] и может быть выражена в обратных секундах, минутах, часах и т. д.;

2) величина k_I не зависит от способа выражения концентрации реагента;

3) в реакциях первого порядка одинаковым промежуткам времени отвечают одинаковые доли прореагировавшего вещества.

Последнее утверждение позволяет ввести понятие период полупревращения.

Периодом полупревращения (t_1/2) называют время, необходимое для превращения половины первоначального количества вещества.

Таким образом, в момент времени t = t_1/2 количество непрореагировавшего вещества составляет С₀. В этом случае:

.

(10)

Из данной формулы следует, что в реакциях первого порядка период полупревращения не зависит от начальной концентрации реагента.

В некоторых случаях удобно использовать формулу:

,

(11)

которая позволяет определить время, за которое превращению подвергнется определенное количество исходного вещества.

В организме человека процессы метаболизма лекарственных препаратов протекают, в основном, в соответствии с уравнением реакции первого порядка. Период, за который превращению подвергается половина действующего начала препарата называется периодом полувыведения или полуэлиминации. Зная величины k_I и t_1/2, можно рассчитать оптимальные промежутки времени между приемами лекарственного средства.

Кинетические уравнения реакций различного порядка представлены в табл. 2.

 

Табл. 2. Кинетические уравнения реакций различного порядка.

Порядок реакции	Кинетическое уравнение	Решение кинетического уравнения*	Период полупревращения

* при равных исходных концентрациях реагирующих веществ

 

Из приведенных уравнений следует, что для реакций различного порядка константы скорости имеют неодинаковые размерности. Действительно, константа скорости реакции второго порядка имеет размерность [л·моль^-1·время^-1)], третьего порядка - [л²·моль^-2·время^-1].

Таким образом, сравнивать значения констант скорости реакций различного порядка нельзя.