
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение тесноты и силы корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для измерения тесноты и силы связи между факторным и результативным признаками рассчитывают специальные показатели – эмпирический коэффициент детерминации Эмпирический коэффициент детерминации
где
Значения показателя Общая дисперсия
где yi – индивидуальные значения результативного признака;
n – число единиц совокупности. Общая средняя
или как средняя взвешенная по частоте групп интервального ряда:
Для вычисления Расчет
Для расчета общей дисперсии Таблица 12 Вспомогательная таблица для расчета общей дисперсии
Расчет общей дисперсии по формуле (10):
Общая дисперсия может быть также рассчитана по формуле
где
Для демонстрационного примера
Тогда
Межгрупповая дисперсия
где
k – число групп. Для расчета межгрупповой дисперсии Таблица 13 Вспомогательная таблица для расчета межгрупповой дисперсии
Расчет межгрупповой дисперсии
Расчет эмпирического коэффициента детерминации
Вывод. 75,1% вариации суммы прибыли банков обусловлено вариацией объема кредитных вложений, а 24,9% – влиянием прочих неучтенных факторов. Эмпирическое корреляционное отношение
Значение показателя изменяются в пределах
Таблица 14 Шкала Чэддока
Расчет эмпирического корреляционного отношения
Вывод. Согласно шкале Чэддока связь между объемом кредитных вложений и суммой прибыли банков является тесной. 3. Оценка статистической значимости коэффициента детерминации Показатели Проверка выборочных показателей на их неслучайность осуществляется в статистике с помощью тестов на статистическую значимость (существенность) показателя. Для проверки значимости коэффициента детерминации
где n – число единиц выборочной совокупности,
Величина
где Для проверки значимости показателя Если Fрасч>Fтабл, коэффициент детерминации Если Fрасч<Fтабл, то показатель Фрагмент таблицы Фишера критических величин F-критерия для значений
Расчет дисперсионного F-критерия Фишера для оценки Fрас ч Табличное значение F-критерия при
Вывод: поскольку Fрасч>Fтабл, то величина коэффициента детерминации Задание 3 По результатам выполнения Задания 1 с вероятностью 0,954 необходимо определить: 1) ошибку выборки средней величины объема кредитных вложений банков и границы, в которых будет находиться генеральная средняя. 2) ошибку выборки доли банков с объемом кредитных вложений 175 млн руб. и выше, а также границы, в которых будет находиться генеральная доля. 3) необходимый объем выборки при заданной предельной ошибке выборки, равной 10 млн руб. Выполнение Задания 3 Целью выполнения данного Задания является определение для генеральной совокупности коммерческих банков региона границ, в которых будут находиться величина среднего объема кредитных вложений банков и доля банков с объемом кредитных вложений не менее 175 млн руб.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 697; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.67.248 (0.009 с.) |

 и эмпирическое корреляционное отношение
и эмпирическое корреляционное отношение  .
. , (9)
, (9) – общая дисперсия признака Y,
– общая дисперсия признака Y, – межгрупповая (факторная) дисперсия признака Y.
– межгрупповая (факторная) дисперсия признака Y. . При отсутствии корреляционной связи между признаками Х и Y имеет место равенство
. При отсутствии корреляционной связи между признаками Х и Y имеет место равенство  , (10)
, (10)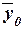 – общая средняя значений результативного признака;
– общая средняя значений результативного признака; вычисляется как средняя арифметическая простая по всем единицам совокупности:
вычисляется как средняя арифметическая простая по всем единицам совокупности: (11)
(11) (12)
(12) по формуле (11):
по формуле (11):

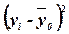


 ,
,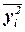 – средняя из квадратов значений результативного признака,
– средняя из квадратов значений результативного признака, – квадрат средней величины значений результативного признака.
– квадрат средней величины значений результативного признака.


 от общей средней
от общей средней  . Показатель
. Показатель  , (13)
, (13) –групповые средние,
–групповые средние, –число единиц в j-ой группе,
–число единиц в j-ой группе,
 в группе
в группе



 или 75,1%
или 75,1% оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле (14)
(14) . Чем ближе значение
. Чем ближе значение 
 и
и  рассчитаны для выборочной совокупности, т.е. на основе ограниченной информации об изучаемом явлении. Поскольку при формировании выборки на первичные данные могли иметь воздействии какие-либо случайные факторы, то есть основание полагать, что и полученные характеристики связи
рассчитаны для выборочной совокупности, т.е. на основе ограниченной информации об изучаемом явлении. Поскольку при формировании выборки на первичные данные могли иметь воздействии какие-либо случайные факторы, то есть основание полагать, что и полученные характеристики связи  ,
, m – количество групп,
m – количество групп, – межгрупповая дисперсия,
– межгрупповая дисперсия,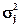 – дисперсия j-ой группы (j=1,2,…,m),
– дисперсия j-ой группы (j=1,2,…,m),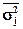 – средняя арифметическая групповых дисперсий.
– средняя арифметическая групповых дисперсий.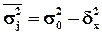 ,
, – общая дисперсия.
– общая дисперсия. и параметров k1, k2, зависящих от величин n и m: k1=m-1, k2=n-m. Величина Fтабл для значений
и параметров k1, k2, зависящих от величин n и m: k1=m-1, k2=n-m. Величина Fтабл для значений  , k1, k2. Уровень значимости
, k1, k2. Уровень значимости  =473,0763,
=473,0763, 



