
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение моды и медианы полученного интервального ряда распределения графическим методом и путем расчетовСодержание книги
Поиск на нашем сайте
Мода и медиана являются структурными средними величинами, характеризующими (наряду со средней арифметической) центр распределения единиц совокупности по изучаемому признаку. Мода Мо для дискретного ряда – это значение признака, наиболее часто встречающееся у единиц исследуемой совокупности[1]. В интервальном вариационном ряду модой приближенно считается центральное значение модального интервала (имеющего наибольшую частоту). Более точно моду можно определить графическим методом по гистограмме ряда (рис.1).
Рис. 1 Определение моды графическим методом Конкретное значение моды для интервального ряда рассчитывается по формуле:
где хМo – нижняя граница модального интервала, h –величина модального интервала, fMo – частота модального интервала, fMo-1 – частота интервала, предшествующего модальному, fMo+1 – частота интервала, следующего за модальным. Согласно табл.1.3 модальным интервалом построенного ряда является интервал 140 – 190 млн. руб., так как его частота максимальна (f3 = 12). Расчет моды по формуле (3):
Вывод. Для рассматриваемой совокупности банков наиболее распространенный объем кредитных вложений характеризуется средней величиной 173,33 млн руб. Медиана Ме – это значение признака, приходящееся на середину ранжированного ряда. По обе стороны от медианы находится одинаковое количество единиц совокупности. Медиану можно определить графическим методом по кумулятивной кривой (рис. 2). Кумулята строится по накопленным частотам (табл. 5, графа 5).
Рис. 2. Определение медианы графическим методом Конкретное значение медианы для интервального ряда рассчитывается по формуле:
где хМе – нижняя граница медианного интервала, h – величина медианного интервала,
fМе – частота медианного интервала, SMе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному. Для расчета медианы необходимо, прежде всего, определить медианный интервал, для чего используются накопленные частоты (или частости) из табл. 5 (графа 5). Так как медиана делит численность ряда пополам, она будет располагаться в том интервале, где накопленная частота впервые равна полусумме всех частот В демонстрационном примере медианным интервалом является интервал 140 – 190 млн. руб., так как именно в этом интервале накопленная частота Sj = 21 впервые превышает величину, равную половине численности единиц совокупности ( Расчет значения медианы по формуле (4):
Вывод. В рассматриваемой совокупности банков половина банков имеют в среднем объем кредитных вложений не более 165 млн руб., а другая половина – не менее 165 млн руб. Расчет характеристик ряда распределения Для расчета характеристик ряда распределения Таблица 6 Расчетная таблица для нахождения характеристик ряда распределения
Расчет средней арифметической взвешенной:
Расчет дисперсии:
Расчет среднего квадратического отклонения:
Расчет коэффициента вариации:
Вывод. Анализ полученных значений показателей Значение Vσ = 29,5% не превышает 33%, следовательно, вариация кредитных вложений в исследуемой совокупности банков незначительна и совокупность по данному признаку качественно однородна. Расхождение между значениями
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.104.106 (0.009 с.) |


 (3)
(3)

 , (4)
, (4)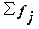 – сумма всех частот,
– сумма всех частот, или превышает ее (т.е. все предшествующие накопленные частоты меньше этой величины).
или превышает ее (т.е. все предшествующие накопленные частоты меньше этой величины). =
=  ).
).
 , σ, σ 2, Vσ на основе табл. 5 строится вспомогательная табл. 6 (
, σ, σ 2, Vσ на основе табл. 5 строится вспомогательная табл. 6 ( – середина j-го интервала).
– середина j-го интервала).




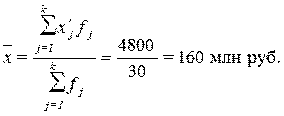 (5)
(5) (6)
(6)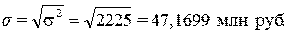
 (7)
(7) ).
).


