
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели измерения тесноты и силы связиСодержание книги
Поиск на нашем сайте
Линейный коэффициент корреляции ( Коэффициент детерминации ( Среднее квадратическое отклонение ( Коэффициентом эластичности (
Тема 4. Модели парной регрессии Определение парной регрессии. Парная регрессия в явном и неявном виде. Понятия регрессанта и регрессора. Виды: линейная и нелинейная. Причины широкой распространенности парной регрессии в моделировании экономических процессов. Методы выбора вида парной регрессии: графический (фактическая линия процесса, средняя линия стохастической полосы, генеральная линия процесса), аналитический (на базе изучения экономической природы связи исследуемых признаков) и экспериментальный (на основе сравнения величины остаточной дисперсии). Этапы их осуществления. Тема 5 Смысл и оценка параметров линейной регрессии. Метод наименьших квадратов Параметры линейной регрессии Метод наименьших квадратов (МНК) для оценки параметров линейной регрессии. Итоговые формулы для расчета параметров. Коэффициент регрессии его интерпретация, величина и знак. Параметр а и возможности его интерпретации. Способы оценивания и значение оценки. Математическое ожидание: дискретной, непрерывной и эмпирической величины. Дисперсия теоретическая и выборочная. Среднеквадратическое отклонение. Ковариация. Тема 6. Статистическая проверка гипотезы Статистическая гипотеза ( Оценка значимости уравнения линейной регрессии. Расчет суммы квадратов отклонений (общей, объясненной регрессией и остаточной) и определение степеней свободы для каждой из них. Дисперсия на одну степень свободы (общая, факторная и остаточная).
Оценка значимости параметров регрессии ( Оценка значимости линейного коэффициента корреляции. Расчет величины ошибки коэффициента корреляции ( Построение интервального прогноза для линейного уравнения регрессии. Расчет интервальной оценки прогнозного значения Тема 7. Нелинейная регрессия и подбор линеаризующего преобразования Два класса нелинейной регрессии: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам и регрессии нелинейные по оцениваемым параметрам. Примеры нелинейных регрессий 1-ого класса, применяемых в эконометрических исследованиях (полиномы разных степеней, парабола второй степени, равносторонняя гипербола, полулогарифмическая функция). Особенности МНК для них. Нелинейные регрессии 2-ого класса. Внутренне линейные модели и возможности их преобразования в линейный вид. Внутренне нелинейные модели и причины невозможности их сведения к линейным. Примеры нелинейных регрессии 2-ого класса. Особенности методов оценки параметров нелинейной регрессии 2-ого класса. Коэффициент эластичности для нелинейных функций: сущность и формула расчета. Его отличие от коэффициента эластичности для линейной регрессии. Коэффициент эластичности для параболы второго порядка, гиперболы, показательной функции, степенной, полулогарифмической, логистической. Коэффициент корреляции для нелинейной функции, особенности его расчета. Границы значения коэффициента.
Средняя ошибка аппроксимации: определение, формула расчета, единицы измерения.
Тема 8.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.235.195 (0.008 с.) |

 ). Возможные модификации формулы его расчета. Границы коэффициента корреляции. Графическая интерпретация Экономический смысл.
). Возможные модификации формулы его расчета. Границы коэффициента корреляции. Графическая интерпретация Экономический смысл.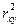 ). Формулы его расчета.
). Формулы его расчета. ), его взаимосвязь с коэффициентом детерминации и экономическая интерпретация.
), его взаимосвязь с коэффициентом детерминации и экономическая интерпретация. ). Формулы расчета. Экономическая интерпретация.
). Формулы расчета. Экономическая интерпретация. и
и  . Графическая оценка параметров регрессии. Экономическая смысл параметров.
. Графическая оценка параметров регрессии. Экономическая смысл параметров. ). Статистическая проверка гипотезы. Статистический критерий. Этапы проверки достоверности гипотезы: формулировка основной гипотезы (
). Статистическая проверка гипотезы. Статистический критерий. Этапы проверки достоверности гипотезы: формулировка основной гипотезы ( ); выбор величины уровня значимости (
); выбор величины уровня значимости ( ); выбор функции от результатов наблюдения (выбор критической статистики); определение критических точек; расчет численной величины критической статистики.
); выбор функции от результатов наблюдения (выбор критической статистики); определение критических точек; расчет численной величины критической статистики. -критерий Фишера и вывод о справедливости выдвинутой гипотезы
-критерий Фишера и вывод о справедливости выдвинутой гипотезы  ). Оценка значимости коэффициента регрессии – расчет величины
). Оценка значимости коэффициента регрессии – расчет величины  -критерия для параметра
-критерия для параметра  ). Его экономическая интерпретация. Взаимосвязь
). Его экономическая интерпретация. Взаимосвязь 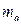 ). Оценка значимости параметра
). Оценка значимости параметра  ).
). ). Определение значения помощью
). Определение значения помощью  ). Взаимосвязь
). Взаимосвязь  и ее графическая интерпретация. Определение величины средней ошибки прогнозируемого индивидуального значения
и ее графическая интерпретация. Определение величины средней ошибки прогнозируемого индивидуального значения  .
.


