
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое изучение взаимосвязи социально – экономических явлений.Содержание книги
Поиск на нашем сайте
В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя корреляционный анализ, а другая - регрессионный анализ. Корреляционная связь – это связь, проявляющаяся при большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и признаками-факторами. Другими словами, корреляционную связь условно можно рассматривать как своего рода функциональную связь средней величины одного признака (результативного) со значением другого (или других). При этом, если рассматривается связь средней величины результативного показателя y с одним признаком-фактором x, корреляция называется парной, а если факторных признаков 2 и более (x1, x2, …, xm) – множественной. По характеру изменений x и y в парной корреляции различают прямую и обратную связь. При прямой связи значения обоих признаков изменяются в одном направлении, т.е. с увеличением (уменьшением) значений x увеличиваются (уменьшаются) и значения y. При обратной связи значения факторного и результативного признаков изменяются в разных направлениях. Изучение корреляционных связей сводится в основном к решению следующих задач: 1) выявление наличия (отсутствия) корреляционной связи между изучаемыми признаками; 2) измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов (эта часть исследования именуется корреляционным анализом); 3) определение уравнения регрессии – математической модели, в которой среднее значение результативного признака у рассматривается как функция одной или нескольких переменных – факторных признаков (эта часть исследования именуется регрессионным анализом). Общий термин «корреляционно-регрессионный анализ» подразумевает всестороннее исследование корреляционных связей (т.е. решение всех трех задач). Для выявления наличия и характера корреляционной связи между двумя признаками в статистике используется ряд методов. 1. Рассмотрение параллельных данных (значений x и y в каждой из n единиц). Единицы наблюдения необходимо расположить по возрастанию значений факторного признака х (как в таблице справа) и затем сравнить с ним (визуально) поведение результативного признака у. 2. Графический метод – это графическое изображение корреляционной зависимости. Для этого, имея n взаимосвязанных пар значений x и y и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x и y. Совокупность полученных точек представляет собой корреляционное поле, а соединяя последовательно нанесенные точки отрезками, получают ломаную линию, именуемую эмпирической линией регрессии. 3. Метод аналитических группировок используется при большом числе наблюдений для выявления корреляционной связи между двумя количественными признаками. Чтобы выявить наличие корреляционной связи между двумя признаками, проводится группировка единиц совокупности по факторному признаку х и для каждой выделенной группы рассчитывается среднее значение результативного признака 4. Метод корреляционных таблиц предполагает комбинационное распределение единиц совокупности по двум количественным признакам. Такая таблица строится по типу «шахматной», т.е. в подлежащем (строках) таблицы выделяются группы по факторному признаку х, а в сказуемом (столбцах) – по результативному у (или наоборот), а в клетках таблицы на пересечении х и у показано число случаев совпадения каждого значения х с соответствующим значением у. На основе аналитических группировок и корреляционных таблиц можно не только выявить наличие зависимости между двумя коррелируемыми показателями, но и измерить тесноту этой связи, в частности, с помощью эмпирического корреляционного отношения.
где m – число групп по факторному признаку х; k – число групп по результативному признаку у;
5. Коэффициент корреляции знаков (Фехнера) – простейший показатель тесноты связи, основанный на сравнении поведения отклонений индивидуальных значений каждого признака (x и y) от своей средней величины. При этом во внимание принимаются не величины отклонений (
Очевидно, что если знаки всех отклонений по каждому признаку совпадут, то КФ= 1, что характеризует наличие прямой связи. Если все знаки не совпадут, то КФ=– 1(обратная связь). Если же åС=åН, то КФ= 0. Итак, как и любой показатель тесноты связи, коэффициент Фехнера может принимать значения от 0 до 6. Линейный коэффициент корреляции – основан на предположении, что при полной независимости признаков x и у отклонения значений факторного признака от средней ( В отличие от КФ в линейном коэффициенте корреляции учитываются не только знаки отклонений от средних величин, но и значения самих отклонений, выраженные для сопоставимости в единицах среднего квадратического отклонения t:
Линейный коэффициент корреляции r представляет собой среднюю величину из произведений нормированных отклонений для x и у:
Линейный коэффициент корреляции может принимать значения от –1 до +1, причем знак определяется в ходе решения. Например, если Таблица 3. Шкала Чэддока
Таким образом, коэффициент корреляции при линейной зависимости служит как мерой тесноты связи, так и показателем, характеризующим степень приближения корреляционной зависимости между х и у к линейной. Поэтому близость значения r к 0 в одних случаях может означать отсутствие связи между х и у, а в других свидетельствовать о том, что зависимость не линейная. 7. Подбор уравнения регрессии представляет собой математическое описание изменения взаимно коррелируемых величин по эмпирическим (фактическим) данным. Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х, не учитывать, т.е. абстрагироваться от них. Другими словами, уравнение регрессии можно рассматривать как вероятностную гипотетическую функциональную связь величины результативного признака у со значениями факторного признака х. Уравнение регрессии можно также назвать теоретической линией регрессии. Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими. Они обычно обозначаются Найти в каждом конкретном случае тип функции, с помощью которой можно наиболее адекватно отразить ту или иную зависимость между признаками х и у, — одна из основных задач регрессионного анализа. Выбор теоретической линии регрессии часто обусловлен формой эмпирической линии регрессии; теоретическая линия как бы сглаживает изломы эмпирической линии регрессии. 8. Коэффициент эластичности показывает, на сколько процентов изменяется в среднем результативный признак y при изменении факторного признака x на 1%. Он рассчитывается на основе уравнения регрессии:
Коэффициент эластичности – величина переменная, т.е. изменяется с изменением значений фактора x. Так, для линейной зависимости
9. Теоретическое корреляционное отношение как универсальный показатель тесноты связи. Измерить тесноту связи между коррелируемыми величинами – значит определить, насколько вариация результативного признака обусловлена вариацией факторного (факторных) признака. Ранее были рассмотрены показатели, с помощью которых можно выявить наличие корреляционной связи между двумя признаками x и y и измерить тесноту этой связи. Наряду с ними существует универсальный показатель – корреляционное отношение (или коэффициент корреляции по Пирсону), применимое ко всем случаям корреляционной зависимости независимо от формы этой связи. Следует различать эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается на основе правила сложения дисперсий как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии, т.е.
Сравнивая вторую дисперсию с первой, получим теоретический коэффициент детерминации:
который показывает, какую долю в общей дисперсии результативного признака занимает дисперсия, выражающая влияние вариации фактора x на вариацию y. Извлекая корень квадратный из коэффициента детерминации, получаем теоретическое корреляционное отношение
Оно может находиться в пределах от 0 до 1, чем ближе его значение к 1, тем теснее связь между вариацией y и x. Для оценки тесноты связи обычно применяется шкала Чэддока (таблица 3). Корреляционное отношение применимо как для парной, так и для множественной корреляции независимо от формы связи. В этом смысле его можно назвать универсальным показателем тесноты связи. При линейной зависимости 9. Коэффициенты корреляции рангов – это менее точные, но более простые по расчету непараметрические показатели для измерения тесноты связи между двумя коррелируемыми признаками. К ним относятся коэффициенты Спирмэна (ρ) и Кендэла (τ), основанные на корреляции не самих значений коррелируемых признаков, а их рангов – порядковых номеров, присваиваемых каждому индивидуальному значению х и у (отдельно) в ранжированном ряду. Оба признака необходимо ранжировать (нумеровать) в одном и том же порядке: от меньших значений к большим и наоборот. Если встречается несколько значений х (или у), то каждому из них присваивается ранг, равный частному от деления суммы рангов (мест в ряду), приходящихся на эти значения, на число равных значений. Ранги признаков х и у обозначают символами Rx и Ry. Если у каждой пары х и у ранги совпадают, это характеризует максимально тесную связь. Если же наблюдается полная противоположность рангов, т.е. в одном ряду ранги возрастают от 1 до n, а в другом – убывают от n до 1, это максимально возможная обратная связь. Подходы для оценки тесноты связи у Спирмэна и Кендэла несколько различаются. Для расчета коэффициента Спирмэна значения признаков х и у нумеруют (отдельно) в порядке возрастания от 1 до n, т.е. им присваивают определенный ранг (Rx и Ry) – порядковый номер в ранжированном ряду. Затем для каждой пары рангов находят их разность (обозначается как d = Rx – Ry), и квадраты этой разности суммируют.
где d – разность рангов х и у; n – число наблюдаемых пар значений х и у. Коэффициент ρ может принимать значения от 0 до ±1. Коэффициент корреляции рангов Кендэла τ строится несколько по-другому, хотя его расчет также начинается с ранжирования значений признаков х и у. Ранги х (Rx) располагают строго в порядке возрастания и параллельно записывают соответствующее каждому Rx значение Ry. Поскольку Rx записаны строго по возрастанию, то ставится задача определить меру соответствия последовательности Ry «правильному» следованию Rx. При этом для каждого Ry последовательно определяют число следующих за ним рангов, превышающих его значение, и число рангов, меньших по значению. Первые («правильное» следование) учитываются как баллы со знаком «+», и их сумма обозначается буквой Р. Вторые («неправильное» следование) учитываются как баллы со знаком «–», и их сумма обозначается буквой Q. Очевидно, что максимальное значение Р достигается в том случае, если ранги y (Ry) совпадают с рангами х (Rx) и в каждом ряду представляют ряд натуральных чисел от 1 до п. Тогда после первой пары значений Rx = 1 и Ry = 1 число превышения данных значений рангов составит (n – 1), после второй пары, где Rx = 2 и Ry = 2, соответственно (п – 2) и т.д. Таким образом, если ранги х и у совпадают и число пар рангов равно n, то
КРАТКИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ РЕШЕНИЯ ЗАДАЧ ПО ТЕМАМ «СОЦИАЛЬНО-ЭКОНОМИЧЕСКОЙ СТАТИСТИКИ», «СИСТЕМЫ НАЦИОНАЛЬНЫХ СЧЕТОВ». Статистика населения. Численность населения на начало каждого года рассчитывается на основе следующего балансового уравнения: t +1 S = t S + N − M + П − B, где t S и t +1 S - численность населения на начало года t и года t+1 соответственно; N - число родившихся u1074 в году t; M - число умерших в году t; П - число прибывших на данную территорию в году t; B - число выбывших с данной территории в году t. В статистике естественное движение населения характеризуется рядом общих и частных коэффициентов, исчисляемых в промилле, то есть на 1000 человек. Общие коэффициенты рассчитываются относительно среднегодовой численности всего населения по формулам: коэффициент рождаемости коэффициент смертности коэффициент естественного движения При этом Чр означает число родившихся людей в году, а Чу — число умерших. У коэффициента естественного движения критериальным значением служит 0, что позволяет характеризовать процесс воспроизводства населения. Положительный коэффициент естественного движения свидетельствует о расширенном воспроизводстве, нулевой – о простом воспроизводстве, а отрицательный – об естественной убыли населения. Подобные выводы можно делать и с помощью коэффициента жизненности (введен Покровским), имеющего критериальное значение 1 и определяемого по формуле
Если коэффициент жизненности больше единицы – расширенное воспроизводство, равен единице – простое воспроизводство, меньше единицы – естественная убыль населения. Дополнительно могут определяться: коэффициент оборота населения коэффициент экономичности воспроизводства Относительно среднегодовой численности населения определяются также коэффициенты браков и разводов, числителем которых служит соответственно количество заключенных и расторгнутых за год браков:
Движение населения может происходить и за счет миграции, показывающей, куда и откуда, в каком количестве происходит перемещение населения в стране и в международном масштабе. Для этого используется коэффициент общего движения населения, определяемый по формуле: КОД=КЕД+КМ, где КМ – коэффициент механического движения путем миграции, определяемый по формуле КМ=1000ЧМ/ где ЧМ – миграционное сальдо в виде разности числа прибывших и убывших людей по данной территории на постоянное проживание (механический приток [миграционный прирост] или отток [снижение] населения). Различают 8 типов общего движения населения: 1. естественный прирост превышает механический отток; 2. естественный прирост превышает механический приток; 3. механический приток больше естественного прироста; 4. механический приток больше естественной убыли; 5. естественная убыль превышает механический приток; 6. естественная убыль превышает механический отток; 7. механический отток больше естественной убыли; 8. механический отток больше естественного прироста. Типы 1-4 свидетельствуют о росте населения территории, а типы 5-8 о сокращении ее населения. Статистика рынка труда. Трудовые ресурсы страны (ТР) – это население в трудоспособном возрасте (за исключением неработающих инвалидов труда и войны I и II групп и лиц, получающих пенсию по возрасту на льготных условиях), а так лица в нетрудоспособном возрасте (подростки и население старше трудоспособного возраста), занятые в экономике. Согласно Трудовому кодексу РФ, трудоспособный возраст для мужчин составляет от 16 до 59, для женщин - от 16 до 54 лет включительно. Количественно ТР представляют собой численность трудоспособного населения в трудоспособном возрасте и работающих лиц за пределами этого возраста. В составе ТР выделяется 3 группы населения: 1) занятое; 2) учащиеся; 3) лица в трудоспособном возрасте, не занятые в экономике. Статистика использует следующие показатели для изучения ТР и структуры всего населения на макроуровне: - общая численность ТР, их состав и отраслевая структура; - динамика (абсолютный прирост, темпы роста и прироста с выделением естественного и механического движения ресурсов); - интенсивность их воспроизводства (соотношение абсолютного прироста трудовых ресурсов за год к средней годовой их численности); - коэффициенты общей (демографической) и пенсионной нагрузки населения в трудоспособном возрасте; - коэффициенты трудоспособности всего населения и населения в трудоспособном возрасте; - коэффициенты занятости всего населения и трудоспособного населения. Экономически активное население (ЭАН), или рабочая сила, – это часть населения в возрасте, установленном для измерения его экономической активности (в России - от 15 до 72 лет), обеспечивающая предложение рабочей силы для производства товаров и услуг. В численность ЭАН включаются лица, занятые в экономике, и безработные. К занятым в экономике относятся лица, которые в рассматриваемый период: а) выполняли работу хотя бы 1 ч в неделю; б) временно отсутствовали на работе (из-за болезни или травмы, ухода за больными, ежегодного отпуска или выходных дней, компенсационного отпуска или отгулов, установленного законом отпуска по беременности, родам и уходу за детьми, обучения, учебного отпуска, отпуска по инициативе администрации, забастовки, других подобных причин); в) выполняли работу без оплаты на семейном предприятии. В классификации статуса занятых выделены следующие группы: - работающие по найму, или наемные работники; - работающие не по найму (работодатели, самостоятельно занятые, члены производственных кооперативов, неоплачиваемые семейные работники). К безработным относятся лица в возрасте от 16 лет и старше, которые в рассматриваемый период: 1) не имели работы (доходного занятия); 2) занимались в разных формах поиском работы или предпринимали шаги к организации собственного дела; 3) были готовы приступить к работе в течение определенного периода времени. При этом учащиеся, студенты, пенсионеры и инвалиды учитываются в качестве безработных, если они активно занимались поиском работы и были готовы приступить к ней. Для общей оценки активности, занятости и безработицы статистика определяет следующие показатели: уровень экономической активности (доля ЭАН в общей численности населения); уровень занятости и безработицы (доля численности соответственно занятого населения и безработных в ЭАН); продолжительность завершенной и незавершенной безработицы (время с момента начала поиска работы до момента трудоустройства - для завершенной безработицы и до момента регистрации безработицы - для незавершенной). Показателем численности трудовых ресурсов на уровне предприятий и организаций выступает списочное число работников (Тсп). В списочный состав работников включаются работники, принятые на постоянную, временную или сезонную работу, как фактически работающие, так и временно отсутствующие на работе по каким-либо причинам. Работники, принятые на работу на неполный рабочий день или неполную рабочую неделю, а также принятые на половину ставки (оклада) в соответствии со штатным расписанием, учитываются в списочном составе за каждый календарный день как целые единицы, включая нерабочие дни недели, обусловленные при приеме на работу. В отдельном списке отражаются, но не учитываются в списочном составе внешние совместители. Не учитываются также работники, работающие по договорам подряда; лица, привлекаемые для выполнения случайных работ; учащиеся профтехучилищ на практике и стажировке; работники, направленные на работу в другую организацию, за границу, на обучение, если за ними не сохраняется заработная плата. Списочный состав работников устанавливается на каждый календарный день периода и определяется как сумма явок и неявок на работу: Тсп=Тяв + Тняв. Численность работников в праздничные и выходные дни принимается равной численности за предыдущий день. Среднесписочная численность работников за месяц определяется как сумма списочной численности работников за все дни месяца, деленная на число календарных дней:
Постоянное изменение численности работников предприятий и организаций называется оборотом рабочей силы. Различают оборот по приему и оборот по выбытию. Выделяется несколько направлений приема работников: по направлению служб занятости и трудоустройства, по инициативе самого предприятия, в порядке перевода с других предприятий, после окончания учебных заведений. Причинами выбытия работников являются: призыв в армию, поступление в учебные заведения, перевод на другие предприятия, окончание сроков договора найма, выход на пенсию, смерть работника, сокращение штата, по собственному желанию, за прогулы и другие нарушения трудовой дисциплины. Названные причины выбытия, кроме двух последних, прямо предусмотрены трудовым законодательством и квалифицируются как необходимый оборот рабочей силы. Увольнения же по собственному желанию, за прогул и другие нарушения трудовой дисциплины связаны с личностью работника и квалифицируются как излишний оборот рабочей силы, или ее текучесть. Поскольку увольнение за прогул и другие нарушения трудовой дисциплины сейчас утратили свою актуальность, статистика ограничивается учетом текучести только в части увольнения работников по собственному желанию. Абсолютными показателями оборота рабочей силы на предприятии выступают число работников, принятых за анализируемый период (Тпр), и число работников, выбывших с предприятия за анализирумый период (Твыб). Сумма этих показателей отражает валовой оборот рабочей силы. Оценка интенсивности оборота предполагает сравнение этих абсолютных величин принятых и выбывших работников со среднесписочной их численностью. Коэффициент приема Статистической практике известен и показатель постоянства рабочей сипы предприятия в виде отношения числа работников, проработавших на предприятии в течение всего года, к списочной численности работников на конец периода. Статистика рабочего времени Рабочее время выражается в человеко-днях и, что более точно, в человеко-часах. Отработанный человеко-час - это час фактической работы одного работника, тогда как отработанный человеко-день отражает всего лишь явку человека на работу независимо от продолжительности рабочего времени. Общая сумма человеко-дней явок и неявок (включая праздничные и выходные дни) всех работников за период называется календарным фондом времени (Тк.ф). Так как Тк.ф за период есть в то же время сумма Тсп за все дни периода, можно получить среднесписочную численность работников Кроме Тк.ф, следует выделить также табельный фонд Тт.ф, максимально возможный фонд Тмв.ф, явочный фонд Тяв.ф. Соотношение между ними следующее: Тт.ф = Тк.ф – Количество праздничных и выходных человеко-дней; Тмв.ф = Тт.ф – Количество человеко-дней очередных отпусков; Тяв.ф = Тмв.ф – Количество человеко-дней неявок. Для полноты картины о фондах времени и их использовании рекомендуется применять балансы рабочего времени (желательно в человеко-часах). При этом особенно наглядными балансы становятся, если они рассчитываются в среднем на одного работника.
Данные баланса позволяют подробно изучить структуру календарного, табельного и максимально возможного фондов рабочего времени и степень использования каждого из них (путем сравнения фактически отработанного времени с соответствующими фондами). Особое внимание при этом обращается на потери рабочего времени.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.240.101 (0.01 с.) |

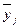 . Если результативный признак у зависит от факторного х, то в изменении среднего значения
. Если результативный признак у зависит от факторного х, то в изменении среднего значения  ,
,
 ,
,
 .
.
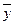 – общее среднее значение результативного признака;
– общее среднее значение результативного признака; – индивидуальные значения результативного признака;
– индивидуальные значения результативного признака; – частота в j -й группе х;
– частота в j -й группе х; 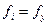 – частота в i -й группе у.
– частота в i -й группе у. ) и (
) и (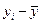 ), а их знаки («+» или «–»). Определив знаки отклонений от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений (С) и несовпадений (Н). Тогда коэффициент Фехнера рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц:
), а их знаки («+» или «–»). Определив знаки отклонений от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений (С) и несовпадений (Н). Тогда коэффициент Фехнера рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц: .
. 1. Однако, если КФ= 1, то это ни в коей мере нельзя воспринимать как свидетельство функциональной зависимости между х и у.
1. Однако, если КФ= 1, то это ни в коей мере нельзя воспринимать как свидетельство функциональной зависимости между х и у.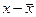 ) носят случайный характер и должны случайно сочетаться с различными отклонениями (
) носят случайный характер и должны случайно сочетаться с различными отклонениями (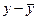 ). При наличии значительного перевеса совпадений или несовпадений таких отклонений делается предположение о наличии связи между x и y.
). При наличии значительного перевеса совпадений или несовпадений таких отклонений делается предположение о наличии связи между x и y. и
и  .
. , или
, или  .
. , то r по формуле будет положительным, что характеризует прямую зависимость между х и у, в противном случае (r< 0) – обратную связь. Если
, то r по формуле будет положительным, что характеризует прямую зависимость между х и у, в противном случае (r< 0) – обратную связь. Если  , то r= 0, что означает отсутствие линейной зависимости между х и у, а при r= 1 – функциональная зависимость между х и у. Следовательно, всякое промежуточное значение r от 0 до 1 характеризует степень приближения корреляционной связи между х и у к функциональной. Существует эмпирическое правило (шкала Чэддока) для оценки тесноты связи, представленное в таблице 3.
, то r= 0, что означает отсутствие линейной зависимости между х и у, а при r= 1 – функциональная зависимость между х и у. Следовательно, всякое промежуточное значение r от 0 до 1 характеризует степень приближения корреляционной связи между х и у к функциональной. Существует эмпирическое правило (шкала Чэддока) для оценки тесноты связи, представленное в таблице 3. или
или 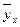 (читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е.
(читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е.  , где
, где  – первая производная уравнения регрессии y по x.
– первая производная уравнения регрессии y по x.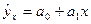 :
: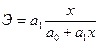 .
. .
.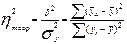 ,
, .
. .
. ,
,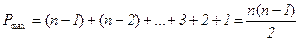 .
. ;
; ;
; .
.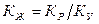 .
. ;
; .
.

 ,
,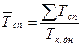
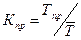 . Коэффициент выбытия (увольнения)
. Коэффициент выбытия (увольнения)  . Коэффициент движения рабочей силы Кдвиж = Кпр – Квыб.
. Коэффициент движения рабочей силы Кдвиж = Кпр – Квыб. .
.


