
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели представления знаний. Формальные логические модели. Продукционные модели.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Знания и данные. Данные – это отдельные факты предметной области, их свойства, в пригодном для машин, обработанном виде. Данными называют формализованную информацию, пригодную для последующей обработки, хранения и передачи средствами автоматизации профессиональной деятельности Данные могут находиться в разных состояниях и трансформироваться из одного вида в другой. D1 – данные как результат наблюдений и измерений(RAW). D2 – данные нематериальных источников информации. D3 – модели, структуры данных в виде в виде таблиц, графиков. D4 – данные на компе в каком либо языке описания. D5 - … база данных. Знания основаны на данных и получаются в результате их обработки, содержат в себе закономерности, опыт специалистов, позволяющий эффективно решать задачи из этой же предметной области. Знания – это формализованная информация, на которую ссылаются и/или которую используют в процессе логического вывода. Z1 – знания в памяти человека, как результат его мышления и деятельности. Z2 – материальные носители. Z3 – поле знаний – это условное описание на каком-либо языке объектов предметной области, их атрибутов и закономерностей их связывающих. Z5 – полноценная база знаний на материальных носителях информации. Основным элементом БЗ является понятие. Существует множество способов определить понятие, но есть два достаточно общих подхода: · Определение понятия через интенсионал – это определение его через соотнесение с объектом более высокого уровня. · Определение понятия через экстенсионал – соотнесение с объектом более низкого уровня с указанием общих свойств. Знания могут быть классифицированы следующим образом: · поверхностные – это знания о видимых взаимосвязях между отдельными событиями и фактами в предметной области · глубинные знания – абстракции, аналогии и схемы, отображающие структуру и природу процессов, протекающих в предметной области. Свойства «превращающие» данные в знания: · Внутренняя интерпретация (интерпретируемость). Это свойство предполагает, что в ЭВМ хранятся, не только собственно (сами) данные, но и данные о данных, что позволяет содержательно их интерпретировать. · Внутренняя структура связей. Предполагается, что в качестве информационных единиц используются не отдельные данные, а их упорядоченные определенными отношениями структуры.
· Внешняя структура связей. Ситуативная связь. · Шкалирование. Предполагает введение соотношений между различными информационными единицами и упорядочение информационных единиц путем измерения интенсивности отношений и свойств. · Семантическая метрика. На практике довольно часто встречаются понятия, к которым неприменимы количественные шкалы, но существует потребность в установлении их близости (понятия «искусственный интеллект» и «искусственный разум»). · Активность. Данное свойство принципиально отличает понятие «знание» от понятия «данные». Например, знания человека, как правило, активны, поскольку ему свойственна познавательная активность. В отличие от данных знания позволяют выводить (получать) новые знания. Будучи активными, знания позволяют человеку решать не только типовые, но и принципиально новые, нетрадиционные задачи. Наука о знаниях называется эпистемологией. В рамках этой науки рассматриваются характер, структура и происхождение знаний.
Модели представления знаний. Формальные логические модели. Продукционные модели. МПЗ – это язык и концептуальная схема для описания знаний в единообразном виде, большинство из них может быть классифицировано на: формальные логические модели; продукционные модели; семантические сети; фреймы. Формальные логические модели – это модели, основанные на формальных исчислениях, в качестве таких исчислений используются различные математ.-логические модели-языки, которые позволяют делать логический вывод на основе имеющихся правил и аксиом. В логических моделях знания представляются в виде совокупности правильно построенных формул какой-либо формальной системы, которая задается четверкой (T,P,A,R): Т – множество базовых элементов; Р– множество синтаксических правил; А – множество аксиом ФС, которые в рамках данной ФС априорно считаются истинными; R – конечное множество правил вывода. В основе ФЛМ лежит понятие высказывание – это атомарное предложение на этом формальном языке. В качестве таких моделей могут использоваться: · пропозициональная логика (простые высказывания +|&→↔)
· логика 1ого порядка (добавляются кванторы общности и существования, предикаты, логические функции) БЗ в таком случае представляет собой множество высказываний. Для получения знаний используются правила логического вывода на основе имеющихся в знаниях высказываниях. Логический вывод – это шаблоны или операции, позволяющие из одних высказываний выводить другие с сохранением истинности и непротиворечивости. Получение знаний может быть разделено на два вида: · в БЗ сообщается новое высказывание, и алгоритм вывода выводит все возможные заключения для этого высказывания. · при сообщении высказывания в БЗ ей нужно доказать истинность/ложность этого утверждения. Был разработан наиб. эфф. алгоритм вывода – метод резолюций. Преимущества данной модели: · высокий уровень формализации. · согласованность знаний как единого целого. · единая система описания как знаний ПО, так и способов решения задач в этой ПО. Недостатки данной модел и: · представление знаний в таких моделях не наглядно. · не эффективно обозначить свойства и отношения однотипными логическими функциями. · описание знаний в виде лог. формул не позволяет проявится преим. которые имеют автоматические системы обработки структур данных. Продукционные модели – модель основанная на правилах, позволяет представлять знания в виде правил «если…, то…». Под условием понимается некоторое предложение-образец, по которому осуществляется поиск в базе знаний. Основным положением ПМ яв множество продукции или правил вывода (Wi, Ui, Pi, Ai→Bi, Ci): Wi – сфера применения i-й продукции; Ui, – предусловие i-й продукции, содержащее информацию об истинности данной продукции; Pi, – условие i-й продукции, истинностное значение которого разрешает применять данную продукцию; Ai→Bi – ядро i-й продукции, «если..., то...»; Ci – постусловие i-й продукции, определяющее изменения, которые необходимо внести в систему продукций. ПМ в таком случае на основе заданного условия поиска должна выдать как промежуточные этапы поиска, так и итоговые заключения. Вывод в такой БЗ может быть прямой (от данных к цели) либо обратный (от цели к данным). В такой системе всегда имеется интерпретатор (реализует функции анализа условий применимости, выполнения и управление выбором продукции) и машина логического вывода – этот подход используется наиболее часто в промышленных экспертных системах. Для подобной системы может быть успешно использован любой алгоритм классификации, в котором множество входных образов разбивается на множество заключений. · система классификаторов · подкрепляющее обучение · алгоритмы поиска · алгоритм A*, алгоритм поиска на графах Достоинства: · Явность и наглядность интерпретации правил; · Простота механизма вывода; · Простота модификации БЗ. Недостатки: · Неоднозначность выбора правил вывода; · Низкая эффективность и негибкость механизма вывода; · Неоднозначность учёта взаимосвязи между отдельными продукциями; · Сложность восприимчивости; · Сложность оценки целостного представления о предметной области. · Реализация этих моделей базируется на языках типа Prolog. Метод резолюций. Метод резолюций - один из методов доказательства, используемый в формальной логике. Его можно применять при построении ответов на вопросы, однако он требует слишком много машинного времени, когда задача сложна. Метод по существу представляет собой "доказательство от противного". Справедливость гипотезы устанавливается доказательством того, что ее отрицание, сопоставленное с аксиомами, или заведомо справедливыми утверждениями, приводит к противоречию. Сначала отрицание гипотезы и аксиомы представляется в рамках логического формализма, т.е. как предложения, являющиеся дизъюнкциями литеров. Затем в множестве аксиом отыскивается аксиома, содержащая такой литерал, который после соответствующих подстановок значений переменных входит в противоречие с каким-либо литералом в отрицании гипотезы. Когда к двум предложениям применяется резолюция, противоречащие друг другу литералы взаимно уничтожаются. Затем та же процедура применяется уже к результирующему предложению и т.д. В конце концов, если исходная гипотеза была справедливой, этот процесс приводит к явному противоречию.
Однако у метода резолюции есть один крупный недостаток: он подвержен явлению " комбинаторного взрыва ", когда число резолюций, проводимых программой, растет экспоненциально как функция сложности задачи. Программы, успешно применяющие метод резолюции на небольших пробных задачах, как правило, не справляются с более интересными задачами реального мира, масштабы которых значительно шире. Однако во многих практических ситуациях вся мощь правила резолюции не требуется. Реальные базы знаний часто содержат только выражения в ограниченной форме, называемые ^ хорновскими выражениями. Хорновское выражение представляет собой дизъюнкцию литералов, среди которых положительным является не больше чем один. p Каждое хорновское выражение может быть записано как импликация, предпосылкой которой является конъюнкция положительных литералов, а заключением— один положительный литерал. Хорновские выражения, подобные этому, имеющие точно один положительный литерал, называются определенными выражениями. Такой положительный литерал называется головой выражения, а отрицательные литералы образуют тело выражения. Определенное выражение без отрицательных литералов просто утверждает справедливость некоторого высказывания; такую конструкцию иногда называют фактом. Хорновское выражение без положительных литералов может быть записано как импликация, заключением которой является литерал False. Логический вывод с использованием хорновских выражений может осуществляться с помощью алгоритма прямого логического вывода и обратного логического вывода, которые рассматриваются ниже. Оба эти алгоритма являются очень естественными в том смысле, что этапы логического вывода являются для людей очевидными и за ними можно легко проследить.
Получение логических следствий с помощью хорновских выражений может осуществляться за время, линейно зависящее от размера БЗ. Этот последний означает, что процедура логического вывода оказывается весьма недорогостоящей. Алгоритм прямого логического вывода начинает работу с известных фактов в БЗ. Если известны все предпосылки некоторой импликации (выражения), то ее заключение добавляется к множеству известных фактов. Этот процесс продолжается до тех пор, пока запрос не выводится как факт, либо дальнейший вывод становится невозможным. Можно легко убедиться в том, что алгоритм прямого логического вывода является непротиворечивым: каждый этап логического вывода по сути представляет собой применение правила отделения. Кроме того, алгоритм прямого логического вывода является полным: в нем может быть получено каждое атомарное высказывание, которое следует из базы знаний. Алгоритм обратного логического вывода действует в обратном направлении от запроса. Если удается сразу же узнать, что выск., содержащееся в запросе q, является истинным, то не нужно выполнять никакой работы. В противном случае алгоритм находит те импликации в базе знаний, из которых следует g. Если можно доказать, что все предпосылки одной из этих импликаций являются истинными, то высказывание g также является истинным. Зачастую стоимость обратного логического вывода намного меньше по сравнению со стоимостью, линейно зависящей от размера базы знаний, поскольку в этом процессе затрагиваются только факты, непосредственно относящиеся к делу. Алгоритм ID3. Один из наиболее ранних алгоритмов обучения деревьев решений, использующих рекурсивное разбиение подмножеств в узлах дерева по одному из выбранных атрибутов. Начинает работу с корня дерева, в котором содержатся все примеры обучающего множества. Для разделения в нем выбирается один из атрибутов, и для каждого принимаемого им значения строится ветвь, и создается дочерний узел, в который распределяются все содержащие его записи. Пусть, например, атрибут принимает три значения:: A, B и C. Тогда при разбиении исходного множества алгоритм создаст три дочерних узла T1(A), T2(B) и T3(C), в первый из которых будут помещены все записи со значением A, во второй – B, а в третий – C. В случае конфликтов, решения принимаются большинством. Процедура повторяется рекурсивно до тех пор, пока в узлах не останутся только примеры одного класса, после чего они будут объявлены листами и ветвление прекратится. Наиболее проблемным этапом здесь является выбор атрибута, по которому будет производиться разбиение. Классический алгоритм ID3 использует для этого критерий увеличения информации или уменьшения энтропии. В общем, алгоритм ID3 следующий: 1. Взять все неиспользованные признаки и посчитать их энтропию относительно тестовых образцов.
2. Выбрать признак, для которого энтропия минимальна (а информационная выгода соответственно максимальна). 3. Сделать узел дерева, содержащий этот признак. Если в качестве критерия используют значение энтропии, не используют эвристик усечения дерева. Алгоритм допускает множественные листья. Практическое применение классической реализации ID3 сталкивается с рядом проблем, характерных для моделей, основанных на обучении вообще и деревьев решений в частности. Основными из них являются переобучение и наличие пропусков в данных. Поэтому алгоритм был усовершенствован, в результате чего появилась его новая версия С4.5. Она позволяет работать с пропущенными значениями признаков, а также имеет меньшую склонность к переобучению. Энтропия. Предположим, что имеется множество А из n элементов, m из которых обладают некоторым свойством S. Тогда энтропия множества А по отношению к свойству S – это H(A,S)=-(m/n)log2(m/n)-(n-m/n)log2(n-m/n). Энтропия зависит от пропорции, в которой разделяется множество. Чем «ровнее» поделили, тем больше энтропия. По мере возрастания пропорции от 0 до ½ - энтропия увеличивается, а после – убывает. Если свойство S не бинарное, а может принимать s различных значений, каждое из которых реализуется в mi случаях, то H(A,S)=-∑(mi/n)log2(mi/n). Энтропия – это среднее количество битов, которые требуются, чтобы закодировать атрибут S у элемента множества A. При выборе атрибута для классификации нужно выбирать его так, чтобы энтропия стала гораздо меньше, при этом энтропия будет разной на разных потомках и выбирать потомка надо с наилучшим вкладом. Предположим, что множество А из n элементов классифицировано посредством атрибута Q, имеющего q возможных значений, тогда прирост информации (уменьшение энтропии) выделится как Gain(A,Q)=H(A,S)-∑от 1 до q(|Ai|/A)H(Ai,S), где Ai – множество элементов А, на которых Q=qi.
Алгоритм C4.5 Алгоритм C4.5 строит дерево решений с неограниченным количеством ветвей у узла. Данный алгоритм может работать только с дискретным зависимым атрибутом и поэтому может решать только задачи классификации. C4.5 считается одним из самых известных и широко используемых алгоритмов построения деревьев классификации. Для работы алгоритма C4.5 необходимо соблюдение следующих требований: · Каждая запись набора данных должна быть ассоциирована с одним из предопределенных классов, т.е. один из атрибутов набора данных должен являться меткой класса. · Классы должны быть дискретными. Каждый пример должен однозначно относиться к одному из классов. · Количество классов должно быть значительно меньше количества записей в исследуемом наборе данных. Алгоритм C4.5 медленно работает на сверхбольших и зашумленных наборах данных. Оба алгоритма являются робастными, т.е. устойчивыми к шумам и выбросам данных. Алгоритмы построения деревьев решений различаются следующими характеристиками: · вид расщепления - бинарное (binary), множественное (multi-way) · критерии расщепления - энтропия, Gini, другие · возможность обработки пропущенных значений · процедура сокращения ветвей или отсечения · возможности извлечения правил из деревьев. Процесс построения дерева будет происходить сверху вниз. На первом шаге мы имеем пустое дерево (имеется только корень) и исходное множество T (ассоциированное с корнем). Требуется разбить исходное множество на подмножества. Это можно сделать, выбрав один из атрибутов в качестве проверки. Тогда в результате разбиения получаются n(по числу значений атрибута) подмножеств и, сответственно, создаются n потомков корня, каждому из которых поставлено в соответствие свое подмножество, полученное при разбиении множества T. Затем эта процедура рекурсивно применяется ко всем подмножествам (потомкам корня) и т.д. Рассмотрим подробнее критерий выбора атрибута. Пусть
Согласно теории информации, количество содержащейся в сообщении информации, зависит от ее вероятности (2ая формула). Поскольку мы используем логарифм с двоичным основанием, то выражение (1) дает количественную оценку в битах. Выражение
дает оценку среднего количества информации, необходимого для определения класса примера из множества T. В терминологии теории информации выражение (2) называется энтропией множества T. Ту же оценку, но только уже после разбиения множества T по X, дает следующее выражение: Тогда критерием для выбора атрибута будет являться следующая формула: Критерий (4) считается для всех атрибутов. Выбирается атрибут, максимизирующий данное выражение. Этот атрибут будет являться проверкой в текущем узле дерева, а затем по этому атрибуту производится дальнейшее построение дерева. Т.е. в узле будет проверяться значение по этому атрибуту и дальнейшее движение по дереву будет производиться в зависимости от полученного ответа Классификация новых примеров Итак, мы имеем дерево решений и хотим использовать его для распознавания нового объекта. Обход дерева решений начинается с корня дерева. На каждом внутреннем узле проверяется значение объекта Y по атрибуту, который соответствует проверке в данном узле, и, в зависимости от полученного ответа, находится соответствующее ветвление, и по этой дуге двигаемся к узлу, находящему на уровень ниже и т.д. Обход дерева заканчивается как только встретится узел решения, который и дает название класса объекта Y.
Достоинства · Высокое качество получаемых моделей, сравнимое с SVM и бустингом, и лучшее, чем у нейронных сетей.[4] · Способность эффективно обрабатывать данные с большим числом признаков и классов. · Нечувствительность к масштабированию (и вообще к любым монотонным преобразованиям) значений признаков. · Одинаково хорошо обрабатываются как непрерывные, так и дискретные признаки. Существуют методы построения деревьев по данным с пропущенными значениями признаков. · Существует методы оценивания значимости отдельных признаков в модели. · Внутренняя оценка способности модели к обобщению (тест out-of-bag). · Высокая параллелизуемость и масштабируемость. Недостатки · Алгоритм склонен к переобучению на некоторых задачах, особенно на зашумленных задачах.[5] · Большой размер получающихся моделей. Требуется O(NK) памяти для хранения модели, где K — число деревьев.
Индекс Gini. Для множества А и свойства S имеющего s значений: Gini=1-∑ [от 1 до s] (|Ai|/|A|) Для набора А и атрибутов Q имеющих q значений и целевого свойства S имеющего s значений: |Q|=q |S|=s Gini(A,Q,S)=Gini(A,S) -∑ [от 1 до q] (|Ai|/|A|)Gini(Ai,S)
Ассоциативные сети. Были разработаны Россом Квиллианом, на основе его исследований восприятия текста человеком. В основе сети лежит создание некоторого мысленного символического представления человеком. Ассоциативная сеть (а.с.) может быть похожа на толковый словарь, в котором каждое понятие определяется другими понятиями из этого словаря. Структура сети включает в себя: узлы-типы, соответствующие какому-либо понятию, которые связаны с определенной комбинацией узлов-лексем, а смысл узла-лексемы определяется через ссылку на соответствующие узлы-типы. В теории а.с. впервые было введено такое понятие как примитивная экономия (св-ва оних объектов наследовались от других). Эта модель получила развитие в а.с. активации. Эти сети были дополнены теорией распространения активации. Эта теория предполагает, что в сети связи имеют различную длину: более короткие определяют более прочные связи, более длинные – связи слабее. Пример:
Теория активации создала предпосылки для разработки древовидных сетей, в которых на самых верхних уровнях находятся более абстрактные понятия, а на более низких – более конкретные:
Модель ассоциативных сетей в 1980-х гг. была формализована и доработана до модели концептуальных графов.
Концептуальные графы. Концептуальный граф (к. г.) – это конечный, связный, двудольный граф(множество вершин которого можно разбить на два непересекающихся подмножества), состоящий из 2-х типов узлов:
Пример: Петя едет в Москву на автобусе.
Для к.г. была разработана формальная семантика, позволяющая описывать тексты любой сложности. Пример: Миша сообщил Жене новости по электронной почте.
Каждый к. г. описывает смысл порождающего его предложения, т. е. должен отвечать на вопрос о чем это предложение. Для этого вводят понятие центральный концепт (сущность предложения). Этапы построения к.г.: 1) Построение начинается с центрального концепта. 2) Определяются понятия связанные с концептом. Любое понятие рассматривается как экземпляр какого-то типа. 3) Совокупность всех типов образует решетку наследования, в которой каждый из типов может иметь множество родителей и мн-во детей. Для обозначения любого не специфицированного экземпляра класса используется обобщенный маркер (*).(В примере вместо Женя - *Х, т. е. Миша отослал сообщение всем). Для указания конкретного экземпляра класса не используя при этом имени объекта служат индексные маркеры, которые позволяют отделить экземпляры от своих имен(В примере: вместо имен - человек). 4) После построения совокупности к. г. для каждого предложения, к ним применяются правила формирования с целью объединения 2 графов в один. Графы можно объединять если одна вершина полностью идентична другой. 5) После объединения итоговый граф подвергается упрощению (исключаются дублирующие отношения). В к.г. вводится специальный тип: высказывание. Объектом ссылки высказывания является мн-во к. г., являющихся подграфами данного графа. Процесс разработки API. Под API понимается доступная функциональность по какой-нибудь задаче или предметной области виде какого-то модуля или группы модулей. Мышление в терминах API повышает качество кода. Хорошие модули используются повторно. Как только модуль становится публичным, то у него появляются пользователи. Проблема в том, что как только появились пользователи, то API изменить нельзя. У модуля должно быть как можно меньше программных пользователей, а с другой стороны наличие большого количества пользователей говорит о том, что ваш код хороший.признаки хорошего API: · Легко изучать и использовать даже без документации · Трудно использовать неправильно · Легко читать и использовать код, который использует API · Легко развивать · Достаточно мощный, чтобы удовлетворять методам · Соответственные аудитории Последовательность разработки API: 1. Сбор сведений Главная задача разработчика на этом этапе собрать реальное требование к системе. Важно не путать предлагаемые решения с реальными требованиями. Необходимо выделить истинные требования в виде примеров использования. Такие примеры использования – это краткое описание того, как ваша задача решается с помощью API. 2. Написание спецификаций Спецификация – это описание требований. Собрав требования, напишите по нему спецификацию не более 1-2 листа. Чем короче спецификация тем легче её переделывать. Далее спецификацию нужно показать как можно большему кол-ву людей, что бы оценить. Как только приобрели уверенность в спецификации – можно программировать. 3. Программирование API Пишем API не обращая внимания на конкретную реализацию. Описывать API нужно как можно раньше и чаще. Начав реализовывать программу, переписывайте API раз за разом, это убережёт от большинства проблем во время тестирования и использования. Пишите комментарии. Основные принципы проектирования API: Цель: API должен делать что-то одно и делать это хорошо. API должен быть минимален, но не меньше необходимого. Делать всё закрытым, открывать только то, что необходимо для решения данной задачи. Реализация не должна влиять на API. В документации должно быть описание программы. Итоги: На последнем этапе (Программирование API)должен получиться прототип API – каркас будущей системы, который состоит из интерфейсов, прототипов классов, методов с комментариями, тестов и примеров использования. 24. Семантические технологии Web (Semantic Web). Определение и общее назначение технологии. Преимущества семантических сетей для интернета. Общее определение понятия семантика - это изучение значений. Семантические технологии Web помогают выделять полезную информацию из данных, содержания документов или кодов приложений, опираясь на открытые стандарты. Если компьютер понимает семантику документа, то это не означает, что он просто интерпретирует набор символов, содержащихся в документе. Это значит, что компьютер понимает смысл документа. При создании интернета (веба) предполагалось, что не только люди будут участвовать в обработке инф-ции, но и машины. Для машин трудно пригодна для обработки информация, представленная в вебе. У машинного робота на данный момент нет никакого алгоритма выделения семантики из текста. Семантический веб - расширение для уже существующей сети, такое, что информация в ней снабжена точно определенным значением. Это позволяет человеку и машине более успешно взаимодействовать. Каноническими примерами поисковых запросов в семантическом вебе явл.: «Где ближайшая библиотека?» С каждым человеком будет ассоциироваться свой собственный поисковый агент, который, опираясь на смысловое содержание страниц будет выполнять замысловатые запросы. Семантический веб будет использоваться для: 1) Семантический поиск – при таком поиске будут выдаваться не те страницы, где встретилось искомое ключевое слово, а лишь те, где есть искомое понятие. 2) Объединение знаний – если будут существовать возможности представления знаний, то интернет превратиться в глобальную БЗ. 3) Всепроникающие вычисления. Семантические технологии Web очерчивают общие рамки, позволяющие осуществлять обмен данными и их многократное использование в различных приложениях, корпорациях и даже сообществах. Семантические технологии Web -это эффективный способ представления данных в интернете. Такую структуру также можно символически отождествить с базой данных, которая связана в глобальном масштабе с содержанием документов в интернете. Причем эта связь осуществляется способом, понятным компьютерам. Семантические технологии представляют значения с помощью онтологии и обеспечивают аргументацию, используя связи, правила, логику и условия, оговоренные в онтологии. К семантическим технологиям Web относятся следующие: 1. Глобальная схема имен (URI); 2. Стандартный синтаксис описания данных (RDF); 3. Стандартные способы описания свойств данных (схема RDF); Стандартные способы описания связей между объектами данных (онтология, определяемая с помощью онтологического языка Web (Web Ontology Language)). Преимущества семантических сетей для интернета: Интернет - это крупнейший из когда-либо существовавших информационных репозиториев, причем его содержание все время растет и представлено на самых разнообразных языках и практически во всех областях знаний. Но в конечном счете становится все труднее находить смысл во всем этом содержимом. Поисковые системы способны находить информацию, содержащую определенные слова, но эта информация не всегда оказывается именно той, что требуется. Какой-то элемент всегда оказывается упущенным. Поиск основан на содержании страниц, но не на семантическом значении этого содержания или информации о странице. Как только будет создан семантический интернет, он даст возможность разметки всего содержания интернета, описания каждого элемента информации и обеспечения семантического значения этих элементов. Таким образом, поисковые системы становятся более эффективными, чем сейчас, а пользователи могут находить именно ту информацию, которая им необходима. Организации, оказывающие различные услуги, способны индексировать их с особым значением. А пользователи будут в состоянии оперативно находить эти услуги, используя программные средства на основе интернета, и использовать их для своей пользы или в сочетании с другими услугами. Data Mining. Классификация. Data mining – это процесс выделения их данных неявной объективной и практически полезной информации и представление ее в виде, пригодном для использования. выделяют 5 стандартных типов закономерностей, которые позволяют выявить методы Data Mining: 1) ассоциация 2) классификация 3) кластеризация 4) Последовательность 5) прогнозирование С помощью классификации выявляются признаки, характеризующие группу, к которой принадлежит тот или иной объект. По этим признакам новый объект можно отнести к той или иной группе. Цель процесса классификации состоит в том, чобы построить модель, которая использует прогнозирующие атрибуты в качестве входных параметров и на выходе получает значение зависимого атрибута. Классификатор – некая сущность, определяющая, какому из предопределенных классов принадлежит объект по вектору признаков. Процесс классификации в общем случае состоит из 2 этапов: 1) Конструирование модели – описание множества предопределенных классов 2) использование модели – классификация новых или неизвестных знаний, оценка правильности и точности модели. Уровень точности – процент правильно классифицированных примеров в тестовом множестве. Тестовое множество не должно зависеть от обучающего множества. Методы, применяемые для решения задач классификации: 1) деревья решений 2) искусственные НС 3) Байесовская классификация 4) метод опорных векторов 5) статистические методы, в частности, линейная регрессия 6) генетические алгоритмы 7) метод ближайшего соседа Точность классификации – оценка уровня ошибок. Оценка точности классификации может производиться при помощи кросс-проверки (процедуры оценки точности классификации на данных из тестового множества и кросс-проверочного множества) Если точность классификации на обучающей выборке примерно равна точности на проверочной, то модель прошла кросс-проверку. Оценивание методов классификации можно проводить из следующих характеристик: 1) скорость создания модели для классификации и скорость ее использования 2) Робастность – устойчивость к данным с помехами 3) Интерпретируемость – возможность понимания модели аналитиком 4) Надежность Data Mining. Кластеризация. Data mining – это процесс выделения их данных неявной объективной и практически полезной информации и представление ее в виде, пригодном для использования. выделяют 5 стандартных типов закономерностей, которые позволяют выявить методы Data Mining: 1) ассоциация 2) классификация 3) кластеризация 4) Последовательность 5) прогнозирование Кластеризация предназначена для разбиения совокупности объектов на отдельные группы. Кластеризация отличается от классификации тем, что сами группы заранее не заданны. DM самостоятельно выделяет группы на основе набора признаков. результатом кластеризации является разбиение на группы. Цель кластеризации – поиск соответствующих структур данных. Кластеризация является описательной процедурой и не делает никаких статистических выводов, но позволяет изучить внутреннюю структуру данных, которые исследуются. Кластером можно считать группу объектов, в которой присутствует: 1) внутренняя однородность 2) Внешняя изолированность Подходы к кластеризации: алгоритмы, основанные на разделении данных (в том числе итеративные): 1) разделение объектов на k-кластеры и итеративное перераспределение объектов для улучшения кластеризации 2) Методы, основанные на концентрации объектов 3) Грит-методы – основаны на квантовании объектов в грит-стуктуры 4)Иерархические алгоритмы, например, агломерация 5) Модельные методы Оценка качества кластеризации: Используются следующие процедуры: 1) ручная провурка 2) Установление контрольных точек и проверка не полученных кластерах 3) Проверка стабильности кластеризации путем добавления новых переменных или объектов 4)Сравнение полученных кластеров с использованием различных методов
Знания и данные. Данные – это отдельные факты предметной области, их свойства, в приго
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 3266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.193.54 (0.022 с.) |

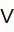 q
q  q
q  n (если
n (если  – количество примеров из некоторого множества S, относящихся к одному и тому же классу Cj. Тогда вероятность того, что случайно выбранный пример из множества S будет принадлежать к классу Cj (1ая формула)
– количество примеров из некоторого множества S, относящихся к одному и тому же классу Cj. Тогда вероятность того, что случайно выбранный пример из множества S будет принадлежать к классу Cj (1ая формула)
 (1)
(1)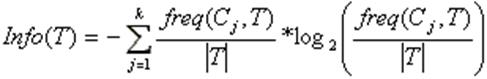 (2)
(2)
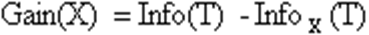


 - концептов (понятий) ()
- концептов (понятий) () - концептуальных отношений ()
- концептуальных отношений ()




