Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деревья решений. Определение, назначение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Деревья решений – один из методов автоматического анализа данных и принятия решений в бизнесе. Деревья решений – это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение. Под правилом понимается логическая конструкция, представленная в виде "если... то...". Область применения деревья решений в настоящее время широка, но все задачи, решаемые этим аппаратом могут быть объединены в следующие три класса: · Описание данных: Деревья решений позволяют хранить информацию о данных в компактной форме, вместо них мы можем хранить дерево решений, которое содержит точное описание объектов. · Классификация: Деревья решений отлично справляются с задачами классификации, т.е. отнесения объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные значения. · Регрессия: Если целевая переменная имеет непрерывные значения, деревья решений позволяют установить зависимость целевой переменной от независимых(входных) переменных. Например, к этому классу относятся задачи численногопрогнозирования(предсказания значений целевой переменной). В узлах дерева, не являвшимися листьями, находятся атрибуты, по которым различаются ситуации. В листьях – значения целевой функции. На ребрах – значения атрибута, из которого исходит это ребро. ДР строятся следующим образом: 1. Выбирается атрибут A и помещается в корень. Для всех значений этого атрибута строим ребра. 2. Выбирается значение целевой функции для измерения значений ребра. ДР не позволяет извлечь какие-либо закономерности из данных, оно позволяет только наиболее эффективно принимать решения и предсказывать значения целевых атрибутов. Цель: построить самое короткое дерево, таким образом, чтобы в его корне стоял наиболее важный атрибут, позволяющий наиболее эффективную классификацию. Достоинства: · быстрый процесс обучения; · генерация правил в областях, где эксперту трудно формализовать свои знания; · извлечение правил на естественном языке; · интуитивно понятная классификационная модель; · высокая точность прогноза, сопоставимая с другими методами (статистика, нейронные сети); · построение непараметрических моделей. В силу этих и многих других причин, методология деревьев решений является важным инструментом в работе каждого специалиста, занимающегося анализом данных, вне зависимости от того практик он или теоретик. Деревья решений являются прекрасным инструментом в системах поддержки принятия решений, интеллектуального анализа данных (data mining). Деревья решений успешно применяются для решения практических задач в следующих областях: · Банковское дело. Оценка кредитоспособности клиентов банка при выдаче кредитов. · Промышленность. Контроль за качеством продукции (выявление дефектов), испытания без разрушений (например проверка качества сварки) и т.д. · Медицина. Диагностика различных заболеваний. · Молекулярная биология. Анализ строения аминокислот.
Алгоритмы обучения деревьев решений. Алгоритм ID3. Критерии разбиений. Обучающий алгоритм является прямым, если он обеспечивает правильные классификации, которые классифицируют еще не встречающиеся примеры. Обучение деревьев решений – обучение с учителем. Состоит из следующих этапов: 1. Вид-разбиение. 2. Критерий расчленения. 3. Процедура сокращения ветвей – отсечение. 4. Тестирование и извлечение правил. Для того, чтобы начать строить или обучать дерево решений необходимо: 1. Собрать множество примеров большого объема. 2. Разделить это множество на два непересекающихся – обучающее и проверочное. 3. применить сам алгоритм для построения текущего дерева решений. 4. определить какой процент примеров в тестовом множестве классифицируется деревом. 5. Если дерево не удовлетворяет, то повторять 2-4 для различных алгоритмов и эвристик. Алгоритм ID3. Один из наиболее ранних алгоритмов обучения деревьев решений, использующих рекурсивное разбиение подмножеств в узлах дерева по одному из выбранных атрибутов. Начинает работу с корня дерева, в котором содержатся все примеры обучающего множества. Для разделения в нем выбирается один из атрибутов, и для каждого принимаемого им значения строится ветвь, и создается дочерний узел, в который распределяются все содержащие его записи. Пусть, например, атрибут принимает три значения:: A, B и C. Тогда при разбиении исходного множества алгоритм создаст три дочерних узла T1(A), T2(B) и T3(C), в первый из которых будут помещены все записи со значением A, во второй – B, а в третий – C. В случае конфликтов, решения принимаются большинством. Процедура повторяется рекурсивно до тех пор, пока в узлах не останутся только примеры одного класса, после чего они будут объявлены листами и ветвление прекратится. Наиболее проблемным этапом здесь является выбор атрибута, по которому будет производиться разбиение. Классический алгоритм ID3 использует для этого критерий увеличения информации или уменьшения энтропии. В общем, алгоритм ID3 следующий: 1. Взять все неиспользованные признаки и посчитать их энтропию относительно тестовых образцов. 2. Выбрать признак, для которого энтропия минимальна (а информационная выгода соответственно максимальна). 3. Сделать узел дерева, содержащий этот признак. Если в качестве критерия используют значение энтропии, не используют эвристик усечения дерева. Алгоритм допускает множественные листья. Практическое применение классической реализации ID3 сталкивается с рядом проблем, характерных для моделей, основанных на обучении вообще и деревьев решений в частности. Основными из них являются переобучение и наличие пропусков в данных. Поэтому алгоритм был усовершенствован, в результате чего появилась его новая версия С4.5. Она позволяет работать с пропущенными значениями признаков, а также имеет меньшую склонность к переобучению. Энтропия. Предположим, что имеется множество А из n элементов, m из которых обладают некоторым свойством S. Тогда энтропия множества А по отношению к свойству S – это H(A,S)=-(m/n)log2(m/n)-(n-m/n)log2(n-m/n). Энтропия зависит от пропорции, в которой разделяется множество. Чем «ровнее» поделили, тем больше энтропия. По мере возрастания пропорции от 0 до ½ - энтропия увеличивается, а после – убывает. Если свойство S не бинарное, а может принимать s различных значений, каждое из которых реализуется в mi случаях, то H(A,S)=-∑(mi/n)log2(mi/n). Энтропия – это среднее количество битов, которые требуются, чтобы закодировать атрибут S у элемента множества A. При выборе атрибута для классификации нужно выбирать его так, чтобы энтропия стала гораздо меньше, при этом энтропия будет разной на разных потомках и выбирать потомка надо с наилучшим вкладом. Предположим, что множество А из n элементов классифицировано посредством атрибута Q, имеющего q возможных значений, тогда прирост информации (уменьшение энтропии) выделится как Gain(A,Q)=H(A,S)-∑от 1 до q(|Ai|/A)H(Ai,S), где Ai – множество элементов А, на которых Q=qi.
Алгоритм C4.5 Алгоритм C4.5 строит дерево решений с неограниченным количеством ветвей у узла. Данный алгоритм может работать только с дискретным зависимым атрибутом и поэтому может решать только задачи классификации. C4.5 считается одним из самых известных и широко используемых алгоритмов построения деревьев классификации. Для работы алгоритма C4.5 необходимо соблюдение следующих требований: · Каждая запись набора данных должна быть ассоциирована с одним из предопределенных классов, т.е. один из атрибутов набора данных должен являться меткой класса. · Классы должны быть дискретными. Каждый пример должен однозначно относиться к одному из классов. · Количество классов должно быть значительно меньше количества записей в исследуемом наборе данных. Алгоритм C4.5 медленно работает на сверхбольших и зашумленных наборах данных. Оба алгоритма являются робастными, т.е. устойчивыми к шумам и выбросам данных. Алгоритмы построения деревьев решений различаются следующими характеристиками: · вид расщепления - бинарное (binary), множественное (multi-way) · критерии расщепления - энтропия, Gini, другие · возможность обработки пропущенных значений · процедура сокращения ветвей или отсечения · возможности извлечения правил из деревьев. Процесс построения дерева будет происходить сверху вниз. На первом шаге мы имеем пустое дерево (имеется только корень) и исходное множество T (ассоциированное с корнем). Требуется разбить исходное множество на подмножества. Это можно сделать, выбрав один из атрибутов в качестве проверки. Тогда в результате разбиения получаются n(по числу значений атрибута) подмножеств и, сответственно, создаются n потомков корня, каждому из которых поставлено в соответствие свое подмножество, полученное при разбиении множества T. Затем эта процедура рекурсивно применяется ко всем подмножествам (потомкам корня) и т.д. Рассмотрим подробнее критерий выбора атрибута. Пусть
Согласно теории информации, количество содержащейся в сообщении информации, зависит от ее вероятности (2ая формула). Поскольку мы используем логарифм с двоичным основанием, то выражение (1) дает количественную оценку в битах. Выражение
дает оценку среднего количества информации, необходимого для определения класса примера из множества T. В терминологии теории информации выражение (2) называется энтропией множества T. Ту же оценку, но только уже после разбиения множества T по X, дает следующее выражение: Тогда критерием для выбора атрибута будет являться следующая формула: Критерий (4) считается для всех атрибутов. Выбирается атрибут, максимизирующий данное выражение. Этот атрибут будет являться проверкой в текущем узле дерева, а затем по этому атрибуту производится дальнейшее построение дерева. Т.е. в узле будет проверяться значение по этому атрибуту и дальнейшее движение по дереву будет производиться в зависимости от полученного ответа Классификация новых примеров Итак, мы имеем дерево решений и хотим использовать его для распознавания нового объекта. Обход дерева решений начинается с корня дерева. На каждом внутреннем узле проверяется значение объекта Y по атрибуту, который соответствует проверке в данном узле, и, в зависимости от полученного ответа, находится соответствующее ветвление, и по этой дуге двигаемся к узлу, находящему на уровень ниже и т.д. Обход дерева заканчивается как только встретится узел решения, который и дает название класса объекта Y.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.92.247 (0.01 с.) |

 – количество примеров из некоторого множества S, относящихся к одному и тому же классу Cj. Тогда вероятность того, что случайно выбранный пример из множества S будет принадлежать к классу Cj (1ая формула)
– количество примеров из некоторого множества S, относящихся к одному и тому же классу Cj. Тогда вероятность того, что случайно выбранный пример из множества S будет принадлежать к классу Cj (1ая формула)
 (1)
(1)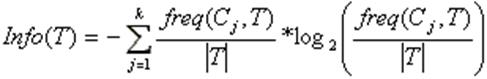 (2)
(2)