
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о вариации признаков.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Вариация признака -изменение признака у ед-ц совокупности (напр. Рабочий различается по возрасту, стажу, квалификации…). Вариация порождается комплексом разнообразных условий, воздействующих на элементы совокупности. Влияющие факторы: внутренние и внешние, необходимые и случайные. Их действие органично переплетено. Напр., поломка строительной машины м. ↓ производить-ть труда, но этого не произойдёт, если будет резервная машина. Следовательно, необходимость оказывает регулирующее значение на случайные факторы. Мерой вариации в некоторой степени является ср-яя ве-на; но при одинаковой ср-ей размеры вариации могут существенно отличаться друг от друга. Поэтому д/характеристики распределения необходимы показатели степени вариации. РЯДЫ РАСПРЕДЕЛЕНИЯ. В процессе группировки производится распределение ед-ц совокупности по значениям группировочного признака. В результате получается 2 колонки: одна содержит перечень значений признака, другая – данные о численности ед-ц. Такое распределение ед-ц совокупности по значению группировочного признака назыв. рядом распределения (РР). РР м.б.образ.по кач.атрибутивным (атрибутивные) и колич.(вариационные) пр-кам. Различают: дискретные вариац.ряды, интервальные вариац.ряды. Чаще примен.интерв.вар.ряды. При их построении след.соблюдать ряд условий: группы и подгруппы д.существенно отличаться др.от др.; лучше применять неравн.инт., а применение равных интервалов даёт возм-ть исп-ть матем. приёмы анализа явлений; чем больше колебание пр-ка, тем больше д.б. групп; не д.б. единичных и нулевых групп. Частоты – абс.численности интервалов ряда. Частоты, выраж.в долях или %тах ряда – частности. В интерв.рядах с неравными интервалами непосредств.сравнение численности затруднено, т.к. меняются и интервалы и их численности. В этом случае опред-ют плотность распред-я (отношение частот или частности к вел-не интервала). Плотность м.б.:абс.(рассчитана на основе частот), относ.(рассчитана по частностям). Частоты в вариац.рядах с равными интерв.и плотностью распред-я в рядах с неравн.интерв.выр-ют опред.закономерность распред-я. Д/харр-ки РР м.исп-ся и накопл.частоты; они д/каждого интерв.ряда рассчит.путём послед. суммир-я частот всех интервалов (рассчит-ся в восходящем и нисходящем порядках). Графич.изобр-е рядов распред-я. Графики!!!!!!!!!!!!!! Д/графического изображения дискретного ряда исп-ся полигон распр-я, гистогр-мы, в ряде случаев кумулятивная кривая. Гистограмма м.б.преобраз.в полигон распр-я путём соед-я середин верхн.сторон прямоуг-ков отрезками прямых. При построении гистогр.д/вариац.ряда с неравн.интерв-ми на ось ординат наносят плотность интервала;тогда высоты прямоуг-ков отраж.плотность распред-я.При ↑ числа набл-ий и ↑ число групп интерво-го ряда, что прив.к ↓ вел-ны интервала; при эт.↑ число сторон и ломанная линия превратится в кривую распред-я (хар-ет вариацию пр-ка и закономерность распр-я частот внутри однокачеств.совок-сти). Показатели центра распр-я. Д/обобщающей хар-ки значения пр-ка в вариац.ряду исп-ся ср.арифм., мода, медиана. Д/дискретн.ряда распр-е ср.рассчит-ся: Х =∑х/n; X =∑xf/∑ f Д/интервального ряда: Х = ∑хцf/∑f, где Хц – середина интервала. Мода и медиана явл-ся описат.срю; они хар-ют вел-ну варианта, занимающую опред.значение в ранжированном вариац.ряду. Мода – наиб.часто встречающаяся вел-на пр-ка в дан.сов-сти. Если встр-ся 2 моды → бимодальное распр-е. Д/интерв.ряда с равными интерв-ми мода опред.по ф-ле: Ме - значение пр-ка, стоящ.в середине ранжир.ряда: Nme = (n+1)/2 = (f+1)/2; где n,f число ед-ц. Д/интерв-го вар.ряда с равн.интервалами Ме.опред.по ф-ле: Моду и медиану можно опред.гр-ки Мода прим.при планир-и массового выпуска одежды и обуви, при изучении товарооборота рынка, наиболее распростр.р-ров з\п и т.п. Мед-на прим-ся при экспертных оценках, при контроле кач-ва пр-ции В симметр.рядах мода и медиана равноправны т.к. Х= моде (Мо) = медиане(Ме). Д/ассиметрических рядов лучше Ме, т.к. она находится между Х и Мо. Показатели вариации. Размах вар-и: Хmax – Xmin; завис.только от крайн.значен, поэт.примен.только д/достаточно однор.сов-сти; нужны пок-тели, учит.колеблемость всех значений пр-ка. Ср.лин.отклонение – ср.арифм.из абс.значений отклонений всех значений пр-ка от ср-ей (d): d = ∑|x- x| /n; d = ∑|x- x| f /∑f Дисперсия (у2): у2= ∑(x- x) 2/n; у2= ∑(x- x)2f/∑f; д/альтернативного ряда: у2= р(1-р)=р*q, где р – доля ед-ц, обладающих определённым признаком, q - доля ед-ц, не обладающих определённым признаком. Ср-ее квадратичное (= стандартное отклонение) (у): у = корень из ∑(x-x)2/n; у =корень из ∑(x- x)2f/∑f; д/умеренно ассиметричного распределения: у=1,25d, d=0,8у Ср-ее линейное и квадратичное отклонения – ве-ны именованные, но даже если они равны между собой, а ср-ие арифм-ие различны, то д/каждой совокупности они имеют различное значение. Поэтому отдельно рассчитывается коэффициент вариации: 1) коэф.осцилляции: V=(R/ x)*100%; коэффициент лин.откл-я: V=(d/ x)*100%; коэф.вар-и: V=(у/ x)*100%. Коэф.вар-и исп-ся не только д/сравнит.оценки вар-и, но и д/хар-ки однор-сти сов-сти. Если он<33%, то совок-сть однородна и её м.хар-ть ср-ей вел-ной. Если сов-сть неоднор., но нужно рассчит-ть пок-ль вар-и. Пок-ль вариации явл-ся мерой надёжности ср-ей. Чем < d, у2, V тем однороднее изучаемая сов-сть и надёжнее получ/ср-ее. Согл.правилу 3ёх у (сигм), в нормально распред-ых или близких к ним рядах распр-я отклонение не превосходит 3 у встреч в 997 случаях из 1000, не > 2 у в 954 случаях из 1000, не > 1 у 683 из 1000. Дисперсия и её св-ва Св-ва дисп-и: · Дисп-я пост.числа =0 · Если все значения пр-ка ↓ или ↑на к-либо число А, то дисп-я от этого не изм-ся, т.е. дисп-ю м.выч.по откл-ям от к-либо пост.числа А · Если все значения пр-ка↓ или ↑в К-раз, то дисп-я от эт.изм-ся в К2-раз, т.е. м.все значения пр-ка уменьшить в К-раз, вычислить дисп-ю, а затем умножить её на это пост.число в квадрате. · Дисп-я пр-ка=разности ср.квадрата значений признака и квадратом их ср-ей: у2= х2 – х 2; x2 =∑x2f/∑f · Расчёт дисп-и (СП-б моментов или от условного нуля): у2=∑(x-a)2*f/∑f -(x -a)2 Правило сложений дисп-й. Общ.вар-я в сов-сти явл-ся рез-том д-я всех причин и измер-ся общей дисп-ей: у2= ∑(x- x)2f/∑f. Вар-и групповых ср. измер-ся откл-ем групповых ср.от общ.ср-ей, и отраж.влияние фактора, по кот.произведена группировка: у2= ∑(xi - x)/n = ∑(xi - x)2*f/∑f, где xi – групповые ср-ие. Остат.или внутригрупповая вар-я выраж.откл-е отдельных значений пр-ков в кажд.группе от их групповых ср, и отраж.влияние всех проч.факторов, кроме положенного в основу груп-вки. Остат.вар-я будет отражать ср.из групповых дисп-й: дi2= ∑(xi- xi)2/ni; уi2 = ∑ уi2fi/∑ fi Общ.вар-я пр-ков сов-сти опред.как сумма вар-й группировочн.ср.и остат.вар-и: у2= д2+ уi2. Суть рав-ва: общ.дисп-я, возник.под возд-ем всех факторов д.б.= сумме всех дисп-й, возникающих за счёт факторов группировки и под влиянием проч.факторов; это равенство известно как правило сложения дисперсий; оно позволяет находить общ.дисп-ю по групп-ым пок-м. Коэф.детерминации (отнош-емежгрупповой дисперсии к общ) = д2/ у2; его значение макс-но и=1 если д2=у2; его значение мин-но и =0, если д2=0
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 539; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.89.197 (0.01 с.) |

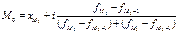 , где ХM0 нач.значение интервала, сод.моду; i – вел-на интервала; FM…- частоты интервалов модального, предшеств.модальному и след-го за модальным.
, где ХM0 нач.значение интервала, сод.моду; i – вел-на интервала; FM…- частоты интервалов модального, предшеств.модальному и след-го за модальным. , где
, где 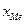 - нач.значение интервала, сод.медиану; i – вел-на равного интервала;
- нач.значение интервала, сод.медиану; i – вел-на равного интервала;  - сумма накопл.частот интервала, предшеств.медианному;
- сумма накопл.частот интервала, предшеств.медианному; 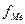 -частота медианного интервала; ∑f =n – число ед-ц
-частота медианного интервала; ∑f =n – число ед-ц


