
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение необх.числ-ти выб-киСодержание книги Поиск на нашем сайте
При провед-и выборочн.набл-я важно определить числ-ть выборочной сов-сти, кот.с опред.вер-тью обеспеч.зада.точность рез-тов. Необх.ф-лы м.получить из ф-л ошибок выборки: 1) д/повторн.отбора: Ошибка выб-ки при типич. При типич.выборке выбир.ед-цы из групп ГС,выдел.по опред.пр-ку, поэт.ошибка выборки будет зависеть от вар-и пр-ка внутри каждой группы. Эта внутригр.вар-я измер-ся ср.из групповых дисп-й.Поэт.при типической выборке в ф-ах ошибки выборки вместо общей дисп-и у2 следует учитывать Ошибка выб-ки при серийн.отборе. При серийн.отборе наиб.часто выб.равновелик.серии. В отобр.сериях произв-ся сплошное набл-е ед-ц,поэт.ошибка выборки завис.от числа отобр.серий и от вар-й ср-их внутри серий,кот. измер-ся межсерийной дисперсией. Если общее число серий ГС R, а число отобранных серий r, то имеем: 1) д/повторн.отбора: Ошибка выб-ки при комбинир.отборе. При комбинир.выборке выборочная сов-ть форм-ся в рез-те ступенчатого отбора. Напр-р, д/изучения успеваемости студ-в фак-та сначала отбир.группы,а затем в кажд.группе случ-но или мех-ки отбирают число студ-ов.Поэт.общая ошибка выборки скл-ся из ошибок на каждой ступени и опр-ся как корень квадратный из суммы ошибок соответств.выборок. Напр-р,при комбинировании серийн.выборки ошибка будет опред-ся по ф-ле: Ошибка выб-ки при малой выб-ке
Распростр-е рез-тов выб-ки на ген.сов-ть Кон.целью выборки явл-ся распростр-е рез-тов выборки на ГС. Сущ-ет 2 сп-ба: 1. способ прямого пересечения; ср.значение вел-ны пр-ка выб.сов-ти умножается на число ед-ц ГС (напр, ср.з/п по выборке на число всех рабочих); 2. способ коэфов; прим-ся в том случае.Когда выборочное набл-е провод-ся д/уточнения резз-тов сплошного;отношение вел-ны пр-ка по выборке к ве-не сплошного набл-я даёт поправочный коэф,на кот.корректируют дан.сплошное набл-е.
ТЕМА 8. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ. Понятие и з-чи корреляции Разл-ют связи: 1) функциональная; связь, при кот.каждому значению факторного пр-ка соотв-ет 1 или неск-ко строго опред.значений результативного пр-ка (напр, Sкруга=ПR2);такие связи хар-ны д/естеств.наук,они явл.точн.и полн, обнаруж-ся на небольшом числе ед-ц; 2) корреляц.связь; связь,при кот.каждому значению факторного пр-ка соотв-ет ср.значение результативного пр-ка при большом числе набл-й; эти связи м.б.приближ, неполн. Кор-ция –соотн-е, соотв-е;отношение связи м/у переменными вел-ми. Выделяют корреляции: 1) парная: y=f (a), y=f(b) (влияние отдельных факторов на изучаемый); 2) множеств: y = f (a,b,c) (влияние неск-ких факторов на изучаемый).В зав-ти от напр-я д-я связи б.: прямая (напр-я изм-я пр-ка совпадают – оба ↑ или ↓, в противн.случ. связь обр. При решении корел-ных з-ч мы заменяем корреляционные связи функциями, выражая их соответствующими уравнениями. По аналитическому выражению связи м.б.: прямолинейными (описыв-ся уравнением прямой), криволин. ( описыв-ся ур-ем параболы,гиперболы …). Требования при изуч-и корреляц-ой связи: 1) однор-сть сов-ти и её колич-ой оценки; м.д/этого применить коэфф-т вар-и; 2) д.б. достаточно большое число набл-й, → происходит взаимопогошение случ.факторов; 3) ограничение числа факторов, кот.д.б.независимо др.от др; 4) д.б. нормальн.хар-р распределения исследуемых признаков; 5) факторы должны иметь количественное выражение, иначе нельзя будет построить модель корреляционной зав-ти; 6) число ед-ц, при изучении корреляц.связи должно быть в 5-6 раз больше,чем пр-ков. При изуч-и коррел-ной связи нужно решить след.з-чи:1) убедиться,что связь м/у пр-ми сущ-ет; 2) измерить ст-нь тесноты связи м/у пр-ми; 3) опред-ть ф-лу связи, т.е. аналит.выраж-е; 4) выявить влияние отдельн.факторов на изучаемый. Определение формы связи. Д/опред-я хар-ра и напр-я связи прим-ся ряд приёмов: 1)метод сопост-я двух || рядов: строится ранжированный ряд по факторн.пр-ку,а результативн.записывается соотв-но своим знач-ям,получ.ряды сравн-ся; недостаток приёма–при большом числе ед-ц получ-ся труднообозримый ряд,трудно обнар.связь; 2) формы связи м.обнар-ть гр-ки;3) на практике изуч-е связей м/у пр-ми часто базир.на большом числе набл-й, мат-лы кот.груп-ся по 2ум взаимосвяз.пр-кам;в рез-те групп-ки оформл-ся в виде корреляц. таблицы или решётки(табл.в подлежащем кот.располаг.значение факторн.пр-ка, а в сказуемом – результативн).Чаще всего строятся интервальные ряды. Вел-на интервала опр-ся по ф-ле: (хmax – хmin) /n, (n=1+3,322 lgN). На основании Корреляц.решётки м.сделать выводы: а) сравнивая значения между пр-ми м. сделать вывод о связи между пр-ми; б) если не рассчитывать ср.вел-ны, то по расположению ед-ц в корреляц.решётке м.сделать вывод о хар-ре,напр-и и тесноте связи: 1) если частоты располаг.от верхнего левого угла к нижн.правому → связь пр, если наоборот → связь обр; 2) чем уже расположена полоса частот, чем связь теснее» в) если частоты располагаются по прямой → связь прямолинейна, по кривой → криволинейна; г) в случае,если все клетки корреляц.решётки окаж.заполненными,нужно устан-ть как расположена осн.масса частот
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.10.75 (0.007 с.) |

 д/альтернат.пр-ков:
д/альтернат.пр-ков:  ; д/бесповт.отбора:
; д/бесповт.отбора:  , д/альтернат.пр-ков:
, д/альтернат.пр-ков:  . Внутригруппировочная вар-я измер.из группировочных дисп-й,поэт.при типичной выборке в ф-лах ошибки выборки вместо общей у2 следует учит-ть
. Внутригруппировочная вар-я измер.из группировочных дисп-й,поэт.при типичной выборке в ф-лах ошибки выборки вместо общей у2 следует учит-ть  , если речь идёт о ср-ей и
, если речь идёт о ср-ей и  , если речь идёт о доле
, если речь идёт о доле , д/доли
, д/доли  ; при бесповт.отборе: д/ср-ей
; при бесповт.отборе: д/ср-ей  , д/доли
, д/доли  ,
,  . По ф-ам сначала опред.общ.числ-ть выборки,а затем объём выборки из кажд. гр-пы,пропорц-но их уд.весу.
. По ф-ам сначала опред.общ.числ-ть выборки,а затем объём выборки из кажд. гр-пы,пропорц-но их уд.весу. 2)д/бесповторного отбора:
2)д/бесповторного отбора: 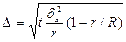
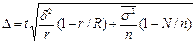
 зачастую на практике применяются малые выборки (n≤30). При малых выборках µ имеет распределение Стьюдента и равно:
зачастую на практике применяются малые выборки (n≤30). При малых выборках µ имеет распределение Стьюдента и равно:  , где
, где 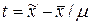 (
(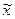 -выборочное,
-выборочное,  -генеральное). Стьюдент доказал, что в случае малой выборки действует особый закон распределения вероятности, здесь ∆ зависит от t и n. По мере роста n распределение в малых выборках стремится к нормальному.
-генеральное). Стьюдент доказал, что в случае малой выборки действует особый закон распределения вероятности, здесь ∆ зависит от t и n. По мере роста n распределение в малых выборках стремится к нормальному.


