
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первое начало термодинамики (ПНТ)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Допустим, что некоторая термодинамическая система (например, газ, заключенный в цилиндр под поршнем), обладая внутренней энергией U1, получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией U2, совершила работу А над внешней средой, т.е. против внешних сил. В этом случае Q=U2-U1+A или Q=DU+A. (4) Уравнение (4) выражает ПНТ: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Для бесконечно малых процессов выражение (4) записывают в дифференциальной форме dQ=dU+dA или в более корректной форме
поскольку только dU является полным дифференциалом, а dQ и dА полными дифференциалами не являются. Из формулы (5) следует, что в СИ количество теплоты выражается в тех же единицах, что работа и энергия, т.е. в джоулях (Дж). Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии DU =0. Тогда, согласно (4) А = Q, т.е. вечный двигатель первого рода, который совершал бы большую работу, чем сообщенная ему извне энергия, не возможен. Это одна из формулировок первого начала термодинамики. Работа газа при изменении его объема
Полная работа при расширении газа от объема V1 до объема V2
Теплоемкость Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
Молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К:
где n=m/M – количество молей вещества. Из (9) и (10) следует, что С = сМ. (11) Применение ПНТ к изопроцессам Изохорический процесс
Таким образом, Изобарический процесс
PV=nRT, запишем ПНТ в дифференциальной форме для изобарического процесса:
Молярная теплоемкость при постоянном давлении
Выражение называется уравнением Майера; оно показывает, что CP всегда больше CV на величину универсальной газовой постоянной R. Это объясняется тем, что для нагревания газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа. Отсюда следует, физический смысл универсальной газовой постоянной R: она численно равна работе, совершаемой одним молем идеального газа при его изобарическом нагревании на 1 К. С учетом (16) первое начало термодинамики для изобарического процесса имеет вид кроме того, Изотермический процесс Для него Т-const. Например, процессы кипения, конденсации, плавления и кристаллизации химически чистых веществ происходят при постоянной температуре, если внешнее давление постоянно.
совершение им работы против внешних сил:
где n=m/M – число молей. Процесс 1-2 (см.рис.5) соответствует изотермическому расширению газа, в этом случае Q12>0 и A12>0. Обратный процесс 2-1 соответствует изотермическому сжатию газа, для него Q12<0 и A12<0. Адиабатический процесс Это процесс, при котором отсутствует теплообмен ( Из ПНТ (
т.е. внешняя работа совершается за счет уменьшения внутренней энергии системы. Учитывая, что
Можно показать, что для адиабатического процесса
Это уравнение называют уравнением адиабаты, g=СP/CV=(i+2)/i - показатель адиабаты, i – число степеней свободы молекулы газа.
изотерма, уравнение которой PV=const. Процесс 3-1-2 соответствует адиабатическому расширению газа. В этом случае Круговые процессы (циклы) Процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние называется круговым процессом или циклом. На диаграмме процессов цикл изображается замкнутой кривой (рис.7).
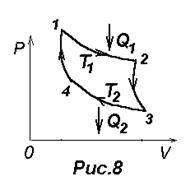
охватываемой замкнутой кривой. Если за цикл совершается положительная работа Прямой цикл используется в тепловых двигателях – периодически действующих двигателях, совершающих работу за счет получения извне теплоты. Обратный цикл используется в холодильных машинах – периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой. В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа DU равно нулю. Поэтому ПНТ (4) для кругового процесса: Q=DU+A=А, т.е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако, в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому A=Q1-Q2, где Q1 - количество теплоты, полученное системой, Q2 - количетво теплоты, отданное системой. Коэффициент полезного действия для кругового процесса h=А/Q=(Q1-Q2)/ Q1= 1- Q2/Q1. (23) Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении и при этом система возвращается в исходное состояние и в окружающей среде и в этой системе не происходит никаких изменений. Например, незатухающие колебания. Заметим, что равновесные процессы называют также обратимыми. Всякий процесс, не удовлетворяющий этим условиям, называется необратимым.(Заметим, что все процессы, сопровождающиеся трением, являются необратимыми). Цикл Карно В 1824 г. французский физик и инженер Н. Карно (1796-1832) опубликовал единственную работу, в которой теоретически проанализировал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат. Его называют циклом Карно, в котором в качестве рабочего тела используют идеальный газ, заключенный в сосуд с подвижным поршнем. Цикл Карно изображен на рис.8, где изотермическое расширение и сжатие заданы соответственно кривыми 1-2 и 3-4, адиабатическое расширение и сжатие – кривыми 2-3 и 4-1.
Обратный цикл Карно положен в основу действия тепловых насосов. Тепловые насосы должны как можно больше тепловой энергии отдавать горячему телу, например системе отопления. Большая часть этой энергии отбирается от окружающей среды с низкой температурой и меньшая часть – получается за счет механической работы, производимой, например компрессором. Энтропия 4.10.1. Энтропия в термодинамике При изучении ПНТ ( Из математики также известно, что величина, на которую надо умножать некоторое выражение, чтобы оно стало полным дифференциалом, называется интегрирующим множителем. В термодинамике доказывается, что для обратимого процесса таким интегрирующим множителем является 1/Т и тогда dQ/Т будет являться полным дифференциалом некоторой пока неизвестной нам функции состояния S системы, т.е. dQ/Т=dS. (25) Определенную таким образом функцию состояния S термодинамической системы называют энтропией, измеряется она в Дж/К. Из (25) видно, что dS и dQ имеют один и тот же знак. Это позволяет по характеру изменения энтропии судить о направлении процесса теплообмена. Понятие энтропии было введено в 1865 г. Клаузиусом. ПНТ (8) для идеального газа произвольной массы m с учетом формул U=(i/2)nRT=nCVT, CV=(i/2)R, PV=nRT (n=m/M – число молей) принимает вид dS = dQ/Т=n(CVdT/T+RdV/V) =n(CVd ln T+Rd ln V) (26) Так как для постоянной массы идеального газа PV/T=const, то ln P +ln V -ln T = const, а d ln P + d ln V - d ln T =0 и выражение (26) можно переписать в двух эквивалентных ему формах dS = n[(CV+R)d ln T-Rd ln P]=n[CP(dT/T)-R(dP/P)], (27) dS = n[(CV+R)d ln V+CVd ln P]=n[CP(dV/V)+CV(dP/P)]. (28) Если система переходит из состояния 1, характеризующегося параметрами P1, V1, T1, в состояние 2, характеризующееся параметрами P2, V2, T2, то изменение энтропии согласно (26) – (28) DS=S2-S1 = = n[CP ln(T2/T1) -R ln(P2/P1)]= n[CP ln(V2/V1)+ CV ln(P2/P1)]. (29) В частности, если процесс круговой, то P2=P1, V2=V1, T2=T1, из (29) следует, что
т.е. действительно dS=dQ/T является полным дифференциалом функции состояния S – энтропии. Так как для адиабатического процесса dQ=TdS=0, то, следовательно, dS=0 и S=const. Таким образом, обратимый адиабатический процесс представляется собой изоэнтропийный процесс. Формулы (26)-(29) позволяют построить термодинамические диаграммы T-S, см. рис.9. Пусть точка О изображает начальное состояние идеального газа, тогда
Изобарический процесс изображен линией 4-4¢, идущей положе изохоры 3-3¢ (0-4 – нагревание и расширение, 0-4¢ – охлаждение и сжатие). Итак, энтропию S можно рассматривать как точно такой же параметр, как и три другие параметра P, V, T. Подобно тому как уравнение состояния идеального газа PV=nRT позволяет выразить, например Т, через другие параметры P и V, так и выражение (29) дает возможность выразить S через другие параметры системы P, V и Т. 4.10.2. Энтропия с кинетической точки зрения. Третье начало термодинамики Энтропия, введенная здесь термодинамически, успешно используется при вычислениях в термодинамике. Однако, существует и другое толкование энтропии. С кинетической точки зрения энтропию лучше всего определить как меру неупорядоченности системы. Когда мы охлаждаем систему (например, газ) при постоянном объеме, мы непрерывно извлекаем из нее тепло и, следовательно, энтропию [см.формулу (25) и ее комментарий], т.е. dQ<0 и dS<0. При этом тепловое движение, которое создает неупорядоченность, становится все менее интенсивным и упорядоченность системы повышается. Когда газ конденсируется в жидкость, молекулы занимают более определенные положения друг относительно друга, в отличие от их положения в газовой фазе. Причем скачкообразное уменьшение беспорядка соответствует скачкообразному уменьшению энтропии. При дальнейшем понижении температуры жидкости тепловое движение, которое создает неупорядоченность, становится все менее интенсивным, и происходит дальнейшее уменьшение энтропии. Когда жидкость отвердевает, молекулы в кристалле занимают вполне определенные положения одна относительно другой, так что неупорядоченность скачком уменьшается. Соответственно при отвердевании выделяется тепло и энтропия также убывает скачком. При абсолютном нуле тепловое движение полностью прекращается, следовательно, неупорядоченность будет также равна нулю. В связи с этим энтропию всех веществ при T=0 принимают равной нулю. Утверждение: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина, т.е. Представление об энтропии как мере неупорядоченности системы хорошо описывает ее зависимость не только от температуры, но и от объема и других параметров системы. 4.10.3. Энтропия в равновесной статистической физике Более глубокий смысл энтропии вскрывается в статистической физике: энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы или число микросостояний, осуществляющих данное макросостояние. По определению W³ 1, т.е. термодинамическая вероятность не есть верояность Р в математическом смысле (Р £1). Например, макросостояние моля кислорода, соответствующее Р =1 физической атмосфере и Т =300К, может быть осуществлено числом микросостояний W = Больцман в 1872 г. показал, что энтропия системы и термодинамическая вероятность связаны между собой следующей формулой S=k ln W, (31) где k – постоянная Больцмана. Для выше приведенного примера S =200 Дж/К.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.68.161 (0.009 с.) |

 , (5)
, (5)












 dl
dl , где S – площадь поршня, Sdl =dV – изменение объема газа. Таким образом,
, где S – площадь поршня, Sdl =dV – изменение объема газа. Таким образом,
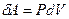 . (6)
. (6)
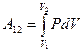 (7)
(7) и графически она изображается площадью фигуры, лежащей под кривой P(V) (Рис.2). Таким образом, работа не определяется только начальным и конечным состояниями газа, а зависит от всего хода процесса. Следовательно, криволинейный интеграл (7) зависит от пути интегрирования и поэтому подынтегральное выражение
и графически она изображается площадью фигуры, лежащей под кривой P(V) (Рис.2). Таким образом, работа не определяется только начальным и конечным состояниями газа, а зависит от всего хода процесса. Следовательно, криволинейный интеграл (7) зависит от пути интегрирования и поэтому подынтегральное выражение  не является полным дифференциалом какой-либо функции состояния газа. С учетом (6) ПНТ можно представить в другой форме
не является полным дифференциалом какой-либо функции состояния газа. С учетом (6) ПНТ можно представить в другой форме  . (8)
. (8)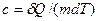 , Дж/(кгК). (9)
, Дж/(кгК). (9) , Дж/(мольК). (10)
, Дж/(мольК). (10)
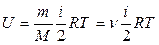 и поэтому
и поэтому 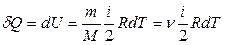 , (12)
и молярная теплоемкость при постоянном объеме
, (12)
и молярная теплоемкость при постоянном объеме
 . (13)
. (13) . (14)
. (14)
 . (15)
. (15) . (16)
. (16)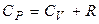 (17)
(17) , (18)
, (18) ,
, 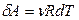 .
.
 =0, так как Т=const и dT=0. Таким образом из ПНТ (
=0, так как Т=const и dT=0. Таким образом из ПНТ ( ) следует, что
) следует, что  , т.е. вся теплота, сообщаемая газу, расходуется на
, т.е. вся теплота, сообщаемая газу, расходуется на
 , (19)
, (19) ) между системой и окружающей средой. К адиабатическим можно отнести все быстропротекающие процессы.
) между системой и окружающей средой. К адиабатическим можно отнести все быстропротекающие процессы. , (20)
, (20)
 . (21)
. (21) . (22)
. (22) , dU <0. Обратный процесс 2-1-3 соответствует адиабатическому сжатию газа. В этом случае
, dU <0. Обратный процесс 2-1-3 соответствует адиабатическому сжатию газа. В этом случае  , dU> 0.
, dU> 0.
 (цикл протекает по ходу часовой стрелки), то он называется прямым (рис.7,а). Если за цикл совершается отрицательная работа
(цикл протекает по ходу часовой стрелки), то он называется прямым (рис.7,а). Если за цикл совершается отрицательная работа  (цикл протекает против хода часовой стрелки), то он называется обратным (рис.7,б). В случае обратного цикла внешние тела совершают над газом положительную работу – работу по сжатию газа А¢. Газ в этом случае совершает отрицательную работу А=-А¢.
(цикл протекает против хода часовой стрелки), то он называется обратным (рис.7,б). В случае обратного цикла внешние тела совершают над газом положительную работу – работу по сжатию газа А¢. Газ в этом случае совершает отрицательную работу А=-А¢.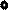
 не зависит от пути интегрирования и, в частности, интеграл по замкнутому пути или контуру L
не зависит от пути интегрирования и, в частности, интеграл по замкнутому пути или контуру L  =0), а dQ и dА не являются полными дифференциалами.
=0), а dQ и dА не являются полными дифференциалами. и полный дифференциал энтропии
и полный дифференциал энтропии = n[CV ln(T2/T1) +R ln(V2/V1)]=
= n[CV ln(T2/T1) +R ln(V2/V1)]= , (30)
, (30) прямая 1-1¢ соответствует изотермическому процессу (0-1 – расширение и уменьшение давления, 0-1¢ - сжатие и увеличение давления). Прямая 2-2¢ соответствует адиабатическому (изоэнтропийному) процессу (0-2 – сжатие и увеличение давления и температуры, 1-2¢ - расширение и уменьшение давления и температуры). Изохорный процесс изображен линией 3-3¢ (0-3 – нагревание и увеличение давления, 0-3¢ - охлаждение и уменьшение давления).
прямая 1-1¢ соответствует изотермическому процессу (0-1 – расширение и уменьшение давления, 0-1¢ - сжатие и увеличение давления). Прямая 2-2¢ соответствует адиабатическому (изоэнтропийному) процессу (0-2 – сжатие и увеличение давления и температуры, 1-2¢ - расширение и уменьшение давления и температуры). Изохорный процесс изображен линией 3-3¢ (0-3 – нагревание и увеличение давления, 0-3¢ - охлаждение и уменьшение давления). называют третьим началом термодинамики или теоремой Нернста-Планка (1906 г, 1910 г).
называют третьим началом термодинамики или теоремой Нернста-Планка (1906 г, 1910 г).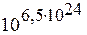 . Представить себе это число совершенно невозможно.
. Представить себе это число совершенно невозможно.


