
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методический анализ структуры и содержания темы «Основы термодинамики»Содержание книги
Поиск на нашем сайте
Методический анализ структуры и содержания темы «Основы термодинамики» Основные задачи изучения темы «Основы термодинамики» Образовательные: формирование знаний и умений применять законы термодинамики и объяснение тепловых процессов. Развивающие: развивать творческое мышление, интеллектуальные способности учащихся; развивать умения наблюдать, анализировать, делать выводы. Воспитательные: развивать коммуникативные качества, сформировать навыки работы в группах, развивать творчество. Структура темы «Основы термодинамики» Структура: 1. 1.Термодинамическая система. 2. 2.Термодинамическое равновесие. 3. Внутренняя энергии, количество теплоты и работа в термодинамике. 4. Внутренняя энергия одноатомного идеального газа. 5. Первый закон термодинамики. 6. Применение первого закона термодинамики к изопроцессам в идеальном газе. 7. Адиабатный процесс. 8. Принцип действия тепловых машин. 9. Тепловые двигатели. 10. Коэффициент полезного действия тепловых двигателей. 11. Экологически проблемы использования тепловых двигателей. Формирование основных видов знаний В ходе изучения темы «Основы термодинамики» учащиеся должны получить теоретические знания и практические умения. Структурные элементы знаний включают в себя основные понятия, физические законы, идеализированные объекты и модели, основные физические величины. Основные понятия: · Термодинамическая система; · Адиабатный процесс; · Нагреватель; · Рабочее тело; · Холодильник; · КПД теплового двигателя; Основные законы: · Первый закон термодинамики Идеализированные объекты: · Идеальный газ; · Макросистема в тепловом равновесии; Основные физические величины: · Внутренняя энергия; · КПД; · Количество теплоты; Формирование основных умений и навыков учебной работы учащихся при изучении темы. Общий уровень умений. Учащийся должен: Иметь представление: · О термодинамическом равновесии; · О необратимости процессов в природе; · О роли тепловых машин в жизни человека и об экологических проблемах их использования; Знать и понимать: · Смысл физических понятий: термодинамическая система, адиабатный процесс, нагреватель, рабочее тело, холодильник, КПД теплового двигателя · Смысл физических законов: первого закона термодинамики; Уметь: · Применять первый закон термодинамики к процессам в идеальном газе; Владеть: · Практическими умениям: решать качественные, графические, расчётные задачи на определение работы, количества теплоты и изменения внутренней энергии идеального газа, КПД тепловых двигателей с использованием первого закона термодинамики, формулы КПД. Особенности изучения содержания темы «Основы термодинамики» Первый закон термодинамики Изучение первого закона термодинамики продолжает формировать представления старшеклассников о фундаментальном естественнонаучном принципе – принципе сохранения энергии. Открытие первого закона термодинамики относится к числу трех крупнейших события 19 в., наряду с открытием клетки и созданием теории Дарвина. В школьном курсе физики первый закон термодинамики изучают как обобщение большого числа опытных данных, установивших соотношение между количеством теплоты, получаемых за счёт работы, и совершённой работой. Прежде чем приступить к изучению первого закона термодинамики, целесообразно повторить закон сохранения энергии в механических процессах, при этом особое внимание уделяют обсуждению вопроса о том, что механическая энергия сохраняется в замкнутых консервативных системах. Если система не является консервативной, то её механическая энергия не сохраняется, она частично или полностью превращается во внутреннюю энергию, но при этом сохраняется полная энергия системы. Далее рассматривают, какими способами можно изменить внутреннюю энергию системы. Этот материал изучали в базовом курсе физики, поэтому здесь его повторяют и обобщают. В результате школьников подводят к выводу: внутреннюю энергию можно изменить либо в процессе теплопередачи, либо при совершении работы, либо про совершении работы и при теплопередаче одновременно. Обсуждают вопрос о мерах измерения внутренней энергии при том или ином процессе. Учащиеся делают вывод: мерой изменения внутренней энергии в процессе совершения работы является работа, а мерой изменения внутренней энергии в процессе теплопередачи – количество теплоты. Здесь же целесообразно повторить вопрос о знаках этих величин. Условились считать количество теплоты положительным ( Работу Рассмотрев ряд примеров, делают вывод: изменение внутренней энергии системы равно сумме количества теплоты, переданного системе, и работе внешних сил над системой:
Количество теплоты, сообщённое системе, идёт на увеличение её внутренней энергии и на совершение системой работы над внешними телами. Анализируя формулу первого закона термодинамики, целесообразно ещё раз подчеркнуть, что внутренняя энергия характеризует состояние системы независимо от способа изменения этого состояния, так как внутренняя энергия системы однозначно определяется параметрами: объёмом После изучения первого закона термодинамики целесообразно разобрать со школьникам ряд упражнений на применение его к конкретным процессам. Например, описать энергетически: 1) Теплообмен между телами в калориметре; 2) нагревание воды на спиртовке; 3) нагревание при ударе. В первом случае система замкнутая и теплоизолированная ( Далее целесообразно рассмотреть примеры применения первого закона термодинамики к изопроцессам в идеальных газах. При изобарном нагревании (рис 1) количество теплоты, переданное системе, идёт на увеличение её внутренней энергии и на совершение системой работы расширения при постоянном давлении. Работа расширения положительна (
При изобарном охлаждении внутренняя энергия системы уменьшается. Количество теплоты, которое система отдаёт равно изменению внутренней энергии системы и работе по сжатию газа. В этом случае и количество теплоты, и работа системы отрицательны. Внутренняя энергия системы уменьшается.
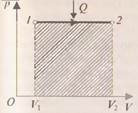
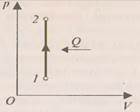
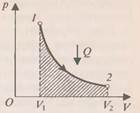
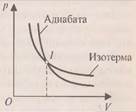
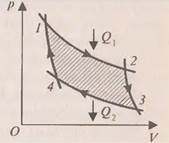
При изотермическом процессе температура постоянна, поэтому При адиабатическом процессе (рис.4) не происходит теплообмена с окружающей средой, поэтому количество теплоты При сжатии внешние силы совершают работу, а газ отрицательную; внутренняя энергия увеличивается, газ нагревается. Из графиков адиабатического и изотермического процессов, изображённых на рис.4, видно, что при адиабатном расширении совершается работа меньшая, чем при изотермическом, а при адиабатном сжатии – большая, чем при изотермическом. Полезно так же с учащимися решать графические задачи, требующие выяснения знаков величин, входящих в формулу первого закона термодинамики, например такую: на рис.5 изображён график зависимости давления от температуры. Как изменяется при этом изменении состояния газа его внутренняя энергия, совершается ли работа, получает или отдаёт система теплоту?
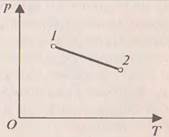 При переходе газа из состояния 1 в состояние 2 давление уменьшается, температура и внутренняя энергия газа увеличиваются. Объём газа также увеличивается ( При переходе газа из состояния 1 в состояние 2 давление уменьшается, температура и внутренняя энергия газа увеличиваются. Объём газа также увеличивается (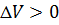 ), следовательно, газ совершает работу расширения, являющуюся положительной. Количество теплоты также положительно ( ), следовательно, газ совершает работу расширения, являющуюся положительной. Количество теплоты также положительно (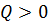 ), следовательно, газ получает некоторое количество теплоты. ), следовательно, газ получает некоторое количество теплоты.
Усвоение первого закона термодинамики способствует и решение вычислительных задач. Рассмотрение применения первого начала термодинамики к изопроцессам создает основу для понимания старшеклассниками принципов работы тепловых двигателей. Работа тепловых двигателей С тепловыми двигателями учащихся знакомят впервые в базовой школе, когда рассматривают общий принцип работы тепловых двигателей (совершение полезной работы за счёт внутренней энергии рабочего тела), изучают двигатель внутреннего сгорания и паровую турбину, а также вводят понятии о КПД тепловых двигателей. Основное внимание уделяют конструкции и принципам работы названных выше двигателей. В курсе физики старших классов рассматривают энергетические процессы, происходящие при работе тепловых двигателей. При изучении принципов работы тепловых двигателей, прежде всего, вводят понятие необратимости, формируют представление о втором законе термодинамики. Понятие необратимости раскрывают с помощью примеров: рассматривают абсолютно упругий удар, как пример обратимого явления, уточнив, что такой удар является идеализацией. Затем обращаются к таким явлениям, как пластическая деформация, диффузия и другие и вводят понятие необратимости процесса как такого, обратный которому самопроизвольно протекать не может. Далее подводят учащихся к формулировке второго закона термодинамики, говорят о том, что осуществить обратный процесс можно только в том случае, ели он будет являться частью другого процесса, связанного с затратами энергии. Так, можно восстановить форму тела при пластической деформации, но для этого необходимы внешние силы и затраты энергии. Изучение принципов работы тепловых двигателей можно построить по следующему плану: - обсуждение вопроса о том, что механическая работа может быть совершена за счёт внутренней энергии; устройство, в котором это происходит, называют тепловым двигателем; - обсуждение вопроса о том, что для непрерывной работы двигатель необходимо возвращать в первоначальное состояние, т.е. он должен быть циклическим; - обсуждение вопроса о том, что для получения положительной работы в первоначальное состояние двигатель должен возвращаться при более низкой температуре, следовательно, он должен иметь нагреватель, рабочее тело и холодильник. Далее учащимся говорят, что рабочее тело (им может быть пар, газ или специальная смесь) получается некоторое количество теплоты
Важным является вопрос о коэффициенте полезного действия. Как известно КПД – это отношение полезной работы к количеству теплоты, полученному от нагревателя:
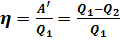 . .
Задача повышения КПД – одна из основных технических задач. Она связана прежде всего с созданием материалов, имеющих достаточную прочность при высоких температурах. В настоящее время температурные границы рабочего тела составляют 303 – 853 K. КПД идеальной машины, работающей по циклу Карно, при таких значениях температур равен 65%. Однако с учётом потерь КПД примерно равен 40%. Необходимо, чтобы школьники поняли принципиальное отличие решения задачи КПД тепловых двигателей от решения этой же задачи применительно к механическим и электрическим двигателям. КПД последних стремятся приблизить к 100%, а КПД тепловых двигателей к КПД идеальной машины Карно, работающей при тех же температурах холодильника и нагревателя. Поэтому повышение КПД тепловых двигателей связано с повышением температуры нагревателя и понижением температуры холодильника. Полезно привести значения мощностей и КПД некоторых тепловых двигателей. Например, карбюраторный двигатель внутреннего сгорания, установленный на автомобиле «Волга ГАЗ-24» имеет мощность 70кВт, КПД около 25%; мощность паровых турбин, установленных на электростанциях, составляет 500-800 МВт, а КПД 40%. В заключение изучения рассматриваемой темы обращают внимание учащихся на значение развития теплоэнергетики для народного хозяйства, в частности рассказывают о той экономии, которую даёт страну развитие теплоэлектроцентралей. Группа – адиабатный Группа – изотермический Группа – изохорный Группа – изобарный
Обратите внимание, адиабата идет обязательно круче изотермы. Ведь при адиабатном процессе давление газа уменьшается не только за счет увеличения объема, как при изотермическом, но и за счет его температуры. Если нагревать тело при постоянном давлении, то оно будет расширяться и совершать работу. Для нагревания тела на 1 К при постоянном давлении ему нужно передать большее количество теплоты, чем при таком же нагревании при постоянном объеме. Как же определить количество теплоты, получаемое телом при нагревании или отданное при охлаждении? Из 8 класса известно, сто Q=cmΔT, где с – удельная теплоемкость вещества. Теплоемкость зависит не только от свойств вещества, но и от процесса, при котором осуществляется теплопередача. Ход урока II. Актуализация знаний. 1. Запишите обозначения следующих величин: – внутренняя энергия 2. Запишите формулу 1 закона термодинамики 6. Запишите формулу 1 закона термодинамики для изобарного процесса 7. Запишите формулу 1 закона термодинамики для изохорного процесса 8. Запишите формулу 1 закона термодинамики для изотермического процесса 9. Запишите формулу 1 закона термодинамики для адиабатного процесса
III. Решение задач. Фронтально (уровень В и С) № 1. Гелий нагревается при постоянном давлении. При этом ему сообщено 20 кДж теплоты. Определить изменение внутренней энергии газа и совершённую им работу. Решение. А/ = рΔV = А/ = 8 кДж, ΔU = 12 кДж. № 2. При адиабатном сжатии 1 моля одноатомного газа внешними силами была совершена работа А. Во сколько раз увеличилась средняя квадратичная скорость молекул этого газа, если начальная температура газа равна Т1? Решение. ΔU = А = U2 - U1, U =
Самостоятельная работа. Вариант 1 А1. Идеальный газ совершил работу 400 Дж, при этом его внутренняя энергия увеличилась на 100 Дж. Чему равно количество теплоты, которое получил или отдал газ в этом процессе? 1) газ получил 500 Дж 3) газ отдал 500 Дж 2) газ получил 300 Дж 4) газ отдал 300 Дж A2. Идеальный одноатомный газ в количестве 6 молей поглощает количество теплоты Q. При этом температура газа повышается на 20 К. Работа, совершаемая газом в этом процессе равна 1 кДж. Поглощённое количество теплоты равно 1) 0,5 кДж 3)1,5 кДж 2) 1 кДж 4)2,5 кДж A3. Идеальный одноатомный газ находится в сосуде с жесткими стенками объёмом 0,6м3. При нагревании его давление возросло на 3.103Па. Насколько увеличилась внутренняя энергия газа? 1) на 0,2 кДж 3) на 0,9 кДж 2) на 1,8 кДж 4) на 2,7 кДж А4. Какое количество теплоты нужно передать молю одноатомного идеального газа, чтобы изобарно увеличить его объём в 3 раза? Начальная температура газа Т0. 1)
1) уменьшилась на 300 кДж 2) увеличилась на 300 кДж 3) уменьшилась на 700 кДж 4) увеличилась на 700 кДж
B1. Установите соответствие между описанными в первом столбце особенностями применения первого закона термодинамики к различным изопроцессам и названием изопроцесса.
С1. Какое количество теплоты получит1 моль идеального одноатомного газа при изобарном нагревании от некоторой начальной температуры и последующем адиабатном расширении, если при адиабатном расширении газ совершает работу А, а в конечном состоянии температура равна начальной?
Вариант 2 А1. Идеальный газ совершил работу, равную 300 Дж. При этом внутренняя энергия увеличилась на 300 Дж. В этом процессе газ… 1) отдал 600 Дж 3) получил 600 Дж 2) отдал 300 Дж 4) получил 300 Дж А2. Внутренняя энергия идеального одноатомного газа U = 300 Дж. Газ занимает объём V = 2л. Давление газа равно… 1) 102 Па 3) 104 Па 2) 103 Па 4) 105 Па A3. Чему равно изменение внутренней энергии газа, если ему передано количество теплоты 500 Дж, а газ при постоянном давлении 105 Па расширился на 3 . 10 – 3 м3? 1) 300 Дж 3) 200 Дж 2) 250 Дж 4) 400 Дж А4. Как изменяется внутренняя энергия идеального газа при повышении его температуры в 2 раза при неизменном объёме 1) увеличивается в 2 раза 2) уменьшается в 2 раза 3) увеличивается в 4 раза 4) уменьшается в 4 раза A5. На рисунке представлен график зависимости давления идеального
Внутренняя энергия при этом 1) уменьшилась на 300 кДж 2) увеличилась на 300 кДж 3) уменьшилась на 700 кДж 4) увеличилась на 700 кДж
В1. Установите соответствие между описанными в первом столбце особенностями применения первого закона термодинамики к различным изопроцессам и названием изопроцесса.
В2. 1 моль инертного газа сжали, совершив работу 600 Дж. В результате сжатия температура газа повысилась на 40°С. Какое количество теплоты отдал газ? Ответ округлите до целых.
изохорно так, что давление падает в п раз. Затем газ расширяется при постоянном давлении. В конечном состоянии его температура равна первоначальной. Молярная масса газа и. Определить совершенную газом работу. VI. Итоги урока. VII. Домашнее задание: повт.§ 11, с.78- VIII. Рефлексия. Список литературы: Физика: учебное пособие для 10 класса общеобразоват. учреждений с рус. яз. обучения / Е.В.Громыко и др. — Минск: Адукацыя i выхаванне, 2013.- 272 с. Вариант 1 1. Запишите формулу средней квадратичной скорости. 2. При температуре 15°С относительная влажность воздуха 80%. Найдите его абсолютную влажность. 3. Молекула азота при нормальных условиях движется со средней скоростью 454 м/с. Определите модуль среднего импульса <p> молекулы. 4. При температуре воздуха -3°С относительная влажность его 40%. Какую массу воды нужно дополнительно испарить в каждый кубометр воздуха, чтобы при температуре 20°С относительная влажность была 90%? 5. В комнате на полу лежит прочный полый шарик радиусом 2 см и массой 10 г. При каком давлении атмосферы p он смог бы всплыть к потолку? Температура в комнате 20°С. Для оценки атмосферу считать идеальным газом. Вариант 2 1. Запишите формулу средней кинетической энергии. 2. Определите массу одной молекулы кислорода. 3. На сколько процентов возрастет средняя квадратичная скорость молекул идеального газа, если абсолютная температура увеличится в n = 2 раза? 4. В комнате объемом 40 м3 при температуре 20°С относительная влажность воздуха 20%. Какую массу воды нужно испарить для увеличения относительной влажности воздуха до 50%? 5. Температура воздуха в комнате 14°С, относительная влажность 60%. В комнате затопили печь, и температура воздуха повысилась до 22°С. Сколько воды надо испарить в комнате, чтобы точка росы при этом увеличилась на 6°С? Какой стала относительная влажность воздуха, если объем комнаты 50 м3? Решение контрольной работы Вариант 1
2) Дано: Решение: t = 15°C φ = 80% ρ = 80*12,8/100 = 10,24 г/м3. ρн = 12,8 г/м3 ρ =? Ответ: ρ = 10,24 г/м3.
<vкв> = 454 м/с <p> = m<vкв>; T = 293 К <p> =? Ответ:
V = 1 м3 ∆m = m2 – m1 t1 = -3°C φ1 = 40% ρн1 = 3,81 г/м3 Аналогично:
φ2 = 90% ρн2 = 17,3 г/м3 ∆m =? Ответ:
r = 2 см mg = ρвgV; m = ρвV; T = 293 К m = 10 г p =? Ответ: Вариант 2 1)
O2 m =? Ответ:
x% =?
Ответ: 41%.
V = 40 м3 ∆m = m2 – m1 t1 = 20°C φ1 = 20% ρн1 = 3,81 г/м3 φ2 = 50% ρн2 = 17,3 г/м3 ∆m =? Ответ:
V = 50 м3 t1 = 14°C φ1 = 60% t2 = 22°C ∆t0 = 6°C ρн1 = 12,1 г/м3; ρн2 = 19,4г/м3;
∆m =? φ2 =? Ответ: План урока 1. Молекулярно-кинетическая трактовка понятия внутренней энергии тела. 2. Вывод формулы внутренней энергии идеального газа. 3. Способы изменения внутренней энергии системы: теплообмен и совершение работы.
Ход урока I. Проверка знаний. (Физический диктант по вопросам: четные – II вариант, нечетные – I вариант.)
1. Что такое микроскопические параметры и что они характеризуют? 2. Что такое макроскопические параметры и что они характеризуют? 3. Наиболее вероятное состояние идеального газа – что это такое? 4. Статистическая закономерность – что это такое? 5. Стационарное равновесное состояние газа – что это такое? 6. Что понимают под температурой тела? 7. Что понимают под средней квадратичной скоростью молекул газа? 8. Что называют давлением газа? 9. Физический смысл постоянной Лошмидта? 10. Какие параметры связывает между собой уравнение Менделеева-Клапейрона? 11. Что называют изопроцессом? 12. Какой процесс называют изотермическим? Какой закон его описывает? 13. Какой процесс называют изобарным? Какой закон его описывает? 14. Какой процесс называют изохорным? Какой закон его описывает? 15. Изобразите изотермический процесс графически в различных координатных осях P-V; V-T; P-T. 16. Изобразите изобарный процесс графически в осях P-V; V-T; P-T. II. Изучение нового материала. Запись в тетрадь: 1. Термодинамика – раздел физики, изучающий возможности использования внутренней энергии тел для совершения механической работы. Термодинамика – макроскопическая теория, так как изучает тепловые свойства макроскопических тел без учета их молекулярного строения. 2. Переход к понятию: внутренняя энергия. Из курса физики 8 класса мы знаем, что внутренняя энергия тела – сумма кинетической энергии хаотического теплового движения частиц (атомов или молекул) тела и потенциальной энергии их взаимодействия. 3. Вывод формулы для расчета внутренней энергии идеального газа. Т.к. En у идеального газа пренебрежимо мала по сравнению с Ek, внутренняя энергия идеального газа определяется кинетической энергией теплового движения частиц.
i – число степеней свободы – число возможных независимых направлений движения молекулы. U – внутренняя энергия. N – число атомов в массе газа.
Используя уравнение Менделеева-Клапейрона, можно формулу для расчета внутренней энергии представить в виде:
поэтому
4. Способы изменения внутренней энергии идеального газа. Ставим перед учащимися проблемный в о п р о с: как можно изменить внутреннюю энергию тела? Чтобы ответить на него, выполняем ряд опытов: 1) нагреваем небольшое количество воды в пробирке, закрытой плотно пробкой; 2) потерли ладони друг о друга, монетку прижали к столу и подвигали по столу. Учащиеся делают в ы в о д: внутреннюю энергию тела можно изменить двумя способами: 1) совершением механической работы; 2) путем теплопередачи. Мерой теплопередачи является количество теплоты
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 1148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.212.203 (0.01 с.) |

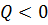 ), если количество теплоты отдано системой.
), если количество теплоты отдано системой.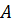 , совершаемую внешними силами над системой, считают положительной (
, совершаемую внешними силами над системой, считают положительной (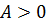 ), если газ сжимается: работа внешних сил отрицательна, если газ расширяется (
), если газ сжимается: работа внешних сил отрицательна, если газ расширяется (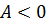 ).
).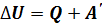 , где
, где 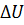 – изменение внутренней энергии, равное разности значений внутренней энергии в конечном и в начальном состояниях. Эту формулу можно записать иначе:
– изменение внутренней энергии, равное разности значений внутренней энергии в конечном и в начальном состояниях. Эту формулу можно записать иначе: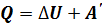 , (
, (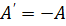 ).
).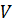 и температурой
и температурой 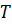 . Работа и количество теплоты характеризуют процесс изменения состояния. При одинаковом изменении состояния эти величины различны (в зависимости от способа перехода системы из одного состояния в другое), хотя сумма их будет одна и та же.
. Работа и количество теплоты характеризуют процесс изменения состояния. При одинаковом изменении состояния эти величины различны (в зависимости от способа перехода системы из одного состояния в другое), хотя сумма их будет одна и та же.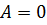 ,
, 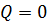 ,
, 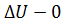 ). Внутренняя энергия системы не изменяется. Во втором случае система замкнутая (
). Внутренняя энергия системы не изменяется. Во втором случае система замкнутая (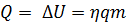 ): изменение внутренней энергии равно количеству теплоты. В третьем случае система теплоизолированная (
): изменение внутренней энергии равно количеству теплоты. В третьем случае система теплоизолированная (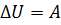 ); изменение внутренней энергии равно совершённой работе.
); изменение внутренней энергии равно совершённой работе.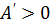 ) и равна
) и равна 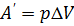 . Из рис.1 видно, что работа численно равна площади заштрихованного прямоугольника, Увеличение внутренней энергии при данном процессе равно:
. Из рис.1 видно, что работа численно равна площади заштрихованного прямоугольника, Увеличение внутренней энергии при данном процессе равно: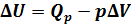 .
.
 При изохорном процессе (рис.2) работа равно нулю, так как объём газа не меняется (
При изохорном процессе (рис.2) работа равно нулю, так как объём газа не меняется (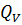 и изменение внутренней энергии положительны, т.е. внутренняя энергия увеличивается, при охлаждении – внутренняя энергия уменьшается.
и изменение внутренней энергии положительны, т.е. внутренняя энергия увеличивается, при охлаждении – внутренняя энергия уменьшается.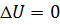 , т.е. внутренняя энергия не изменяется. Если система получает некоторое количество теплоты, то оно идёт на работу, совершаемую газом при расширении. Работа численно равна площади заштрихованной фигуры (рис.3).
, т.е. внутренняя энергия не изменяется. Если система получает некоторое количество теплоты, то оно идёт на работу, совершаемую газом при расширении. Работа численно равна площади заштрихованной фигуры (рис.3).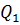 от нагревателя и расширяется. При расширении рабочее тело совершает работу. При сжатии рабочее тело отдаёт количество теплоты
от нагревателя и расширяется. При расширении рабочее тело совершает работу. При сжатии рабочее тело отдаёт количество теплоты 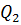 холодильнику. Температуры холодильника и нагревателя поддерживают постоянными, при этом температура нагревателя всегда выше температуры холодильника (
холодильнику. Температуры холодильника и нагревателя поддерживают постоянными, при этом температура нагревателя всегда выше температуры холодильника (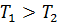 ).
). После этого целесообразно рассмотреть принцип работы идеальной тепловой машины Карно, рабочим телом в которой является идеальный газ. При расширении газа во время его контакта с нагревателем температуру поддерживают постоянной, во время сжатия и контакта с холодильником температура также постоянна, следовательно, расширение и сжатие происходит изотермически (на рис.6 соответственно изотермы 1-2 и 3-4). Но если температура расширения больше температуры сжатия, то необходимо произвести процессы, при которых температура меняется от
После этого целесообразно рассмотреть принцип работы идеальной тепловой машины Карно, рабочим телом в которой является идеальный газ. При расширении газа во время его контакта с нагревателем температуру поддерживают постоянной, во время сжатия и контакта с холодильником температура также постоянна, следовательно, расширение и сжатие происходит изотермически (на рис.6 соответственно изотермы 1-2 и 3-4). Но если температура расширения больше температуры сжатия, то необходимо произвести процессы, при которых температура меняется от 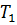 до
до 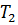 , а затем опять от
, а затем опять от  , ΔU =
, ΔU =  , Q = ΔU + А/ =
, Q = ΔU + А/ = 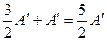 ,
,  , ΔU =
, ΔU =  ,
, , U =
, U =  , A =
, A =  , T2 =
, T2 = 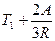
 ,
,  ,
, 
 RT0 2) 3 RT0 3)
RT0 2) 3 RT0 3)  RT0 4) 5RT0
RT0 4) 5RT0 A5. На рисунке представлен график зависимости давления идеального одноатомного газа от его объёма. Газ получил 500 кДж теплоты. Внутренняя энергия при этом
A5. На рисунке представлен график зависимости давления идеального одноатомного газа от его объёма. Газ получил 500 кДж теплоты. Внутренняя энергия при этом В2. Какое количество теплоты выделится при изобарном охлаждении 80 г гелия с 200ºС до 100 ºС? Ответ выразите в килоджоулях (кДж) и округлите до целых.
В2. Какое количество теплоты выделится при изобарном охлаждении 80 г гелия с 200ºС до 100 ºС? Ответ выразите в килоджоулях (кДж) и округлите до целых. одноатомного газа от его объёма. Газ отдал 500 кДж теплоты.
одноатомного газа от его объёма. Газ отдал 500 кДж теплоты. С1. Масса т идеального газа, находящегося при температуре Т, охлаждается
С1. Масса т идеального газа, находящегося при температуре Т, охлаждается 1)
1)  .
. ;
;  ;
; 3) Дано: Решение:
3) Дано: Решение: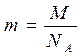 ;
;  ;
; .
. .
. 4) Дано: Решение:
4) Дано: Решение: ;
;  ;
; 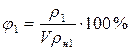 ;
; ;
; t2 = 20°C
t2 = 20°C  ;
; ;
; .
. .
. 5) Дано: Решение:
5) Дано: Решение: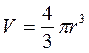 ;
; ;
;  ;
;  ;
; .
.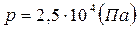 .
. .
. 2) Дано: Решение:
2) Дано: Решение: ;
;  .
.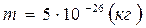 .
. 3) Дано: Решение:
3) Дано: Решение:
 ;
;  ;
;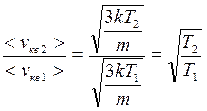 ;
;  ;
;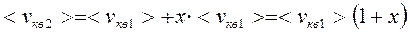 ;
; 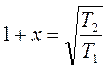 ;
; ;
;  .
. 4) Дано: Решение:
4) Дано: Решение: .
. .
. 5) Дано: Решение:
5) Дано: Решение: ;
; 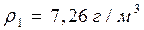 ;
; ;
;  (по таблице);
(по таблице); ;
;  ;
; ;
; .
. ,
, 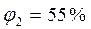 .
. - средняя кинетическая энергия одного атома. В силу хаотичности движения на каждое из трех направлений движения, или степень свободы, по оси X, У, Z приходится одинаковая энергия
- средняя кинетическая энергия одного атома. В силу хаотичности движения на каждое из трех направлений движения, или степень свободы, по оси X, У, Z приходится одинаковая энергия  .
.
 - разделив и умножив это выражение на
- разделив и умножив это выражение на  , получаем:
, получаем: или
или  - внутренняя энергия данной массы идеального газа зависит лишь от одного макроскопического параметра – термодинамической температуры.
- внутренняя энергия данной массы идеального газа зависит лишь от одного макроскопического параметра – термодинамической температуры.  i = 3 – для идеального газа; i = 5 – для двухатомного газа,
i = 3 – для идеального газа; i = 5 – для двухатомного газа, - формулы для внутренней энергии идеального газа.
- формулы для внутренней энергии идеального газа.


