
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второе начало термодинамики (ВНТ)Содержание книги Поиск на нашем сайте
Выражая всеобщий закон сохранения и превращения энергии, первое начало термодинамики (ПНТ) не позволяет определить направление протекания процессов. Действительно, процесс самопроизвольной передачи теплоты от холодного тела к горячему не противоречит ПНТ, если только уменьшение внутренней энергии холодного тела равно энергии, полученной горячим телом. Однако, опыты показывают, что такой процесс не происходит (раскаленный кусок железа, опущенный в воду, не нагревается за счет охлаждения воды). Обобщение огромного экспериментального материала привело к необходимости формулирования второго, третьего и нулевого начал термодинамики. ВНТ в отличие от ПНТ не является всеобщим законом природы. Оно справедливо только по отношению к термодинамическим системам. Существует несколько эквивалентных формулировок ВНТ: 1. Невозможен процесс, единственным результатом которого является передача теплоты от холодного тела к горячему (формулировка Клаузиуса, 1850 г.). 2. Невозможен процесс, единственным результатом которого является совершение работы за счет охлаждения одного тела (формулировка Томсона, 1851 г., в 1892 г Томсон получил титул лорда Кельвина). Соответственно этой формулировке была доказана невозможность вечного двигателя второго рода, который целиком превращал бы в работу теплоту, извлекаемую из окружающих тел (океана, атмосферного воздуха и др.) Согласно формуле (24) для него было бы Q2 =0, A = Q1, h =1. Таким образом, это невозможно. Заметим, что ПНТ не противоречило бы создание такого двигателя. 3. Энтропия изолированной системы не может убывать при любых происходящих в ней процессах, т.е. dS³0, где знак равенства относится к обратимым процессам, а знак больше – к необратимым процессам.(Формулировка Клаузиуса, 1865 г.) В 1876 г. Клаузиус дал наиболее общую формулировку ВНТ: при реальных (необратимых) адиабатических процессах dS>0, т.е. энтропия возрастает, достигая максимального значения в состоянии равновесия. Формула Больцмана (31) S=k ln W позволяет дать статистическое истолкование третьей формулировки ВНТ: Термодинамическая вероятность W состояния изолированной системы при всех происходящих в ней процессах не может убывать. Итак, ВНТ является статистическим законом. Оно выражает необходимые закономерности хаотического движения большого числа частиц, входящих в состав изолированной системы. Лекция 6. Реальные газы. Фазовые переходы Силы и потенциальная энергия межмолекулярных взаимодействий В лекциях 1-2 изучались идеальные газы, молекулы которых имеют пренебрежимо малый собственный объем и не взаимодействуют друг с другом на расстоянии. Свойства реальных газов при высоких давлениях и низких температурах отличаются от свойств идеальных газов, подчиняющихся уравнению Клапейрона-Менделеева. Основная причина этого отличия заключается в том, что во всех телах (твердых, жидких, газообразных) молекулы взаимодействуют друг с другом.
При r>>r0 они практически не взаимодействуют друг с другом. Введем понятие радиуса взаимодействия rВЗ, который определяют приближенно как некоторое расстояние, на котором еще можно считать молекулы взаимодействующими (например, rВЗ =2 r0). При r>>rВЗ можно утверждать, что молекулы не взаимодействуют. Известно, что существуют три основных агрегатных состояния вещества: газ, жидкость и твердое тело. Газ. Он занимает весь предоставленный ему объем; характеризуется тем, что среднее расстояние между молекулами rср >> rВЗ. В газе молекулы между соударениями двигаются, не испытывая никаких сил, прямолинейно и равномерно. Силы действуют на них лишь в момент соударения. Жидкость принимает форму сосуда, в который налита, но сохраняет свой объем. В жидкости молекулы находятся в постоянном взаимодействии, для них rср»rВЗ. Как и в газе, в жидкости молекула не стоит на месте, она совершает хаотическое движение. Твердое тело сохраняет свою форму. Как и в жидкости в твердом теле молекулы сильно взаимодействуют, для них rср»rВЗ. В отличие от жидкости, в твердом теле молекулы закреплены в узлах кристаллической решетки. Тепловое движение проявляется в колебаниях молекулы вокруг положения равновесия. Уравнение Ван-дер-Ваальса (ВдВ) В научной литературе существуют более 150 отличающихся друг от друга уравнений состояния реального газа. Среди них нет ни одного действительно верного и универсального. Остановимся на уравнении ВдВ (1873 г). Он внес в уравнение Клапейрона-Менделеева PV=RT две поправки. Первая поправка связана с действием сил отталкивания между молекулами. Она учитывает собственный объем молекулы V0 и поэтому объем сосуда V заменяют свободным объемом V-b, где b =4 V0NA. В итоге получаем уравнение Клаузиуса для одного моля P = RT/(V-b). (1) Вторая поправка связана с действием сил притяжения между молекулами: в тонком поверхностном слое вблизи стенки сосуда на молекулу, подлетающую к стенке, действует сила притяжения со стороны остальных молекул газа, что приводит к уменьшению силы удара молекулы о стенку сосуда, а, следовательно, и давления на величину DP ~ (P+ a/ которое называют уравнением ВдВ для одного моля газа. В этом уравнении а и b – постоянные, зависящие только от вида газа. Для произвольной массы газа уравнение ВдВ имеет вид (P+ где n=m/M – число молей газа, m – масса газа, M – масса моля. Изотермы Ван-дер-Ваальса Для фиксированных значений Р и Т уравнение (2) есть уравнение третьей степени относительно объема газа V и, следовательно, оно может иметь либо три вещественных корня (V1, V2, V3), либо один вещественных корень (V1) и два комплексно-сопряженных корня (комплексно-сопряженные корни отбрасываем). Поэтому на диаграмме PV (см.рис.2) прямая, параллельная оси V может пересекать изотерму ВдВ либо в трех точках В, D, F, либо в одной K или L. Построение по точкам изотерм ВдВ для трех характерных температур приводит к кривым, изображенным на рис.2. Сначала проведем анализ нижней изотермы ABCDEFG.
Ветви ВС и EF изображают метастабильные состояния вещества (т.е. относительно устойчивые состояния): перегретую жидкость и пересыщенный пар и могут быть осуществлены при определенных условиях. Участок СДЕ ни при каких условиях осуществлен быть не может.
При Т>ТКР газ никаким сжатием нельзя перевести в жидкость. Возвращаясь к анализу изотерм ВдВ, изображенных на рис.2, делаем заключение, что область, ограниченная сверху изотермой НК и справа линией КВМ соответствует жидкой фазе. Область, ограниченная сверху кривой МВКFN, соответствует жидкой и газообразной фазе (жидкость + пар) и область, расположенная правее линии НКFN, соответствует газообразной фазе. При Т>>ТКР и относительно малых давлениях реальные газы ведут себя как идеальные газы. Внутренняя энергия моля реального газа U=CVТ –a/V, (4) т.е. меньше энергии идеального газа U=CVТ. Для произвольной массы реального газа U=n(CVТ –a/V). (5) Фазы и фазовые переходы Фазой называется совокупность частей системы одинаковых по всем физическим, химическим свойствам и структурному составу. Например, существует твердая, жидкая и газообразная фазы (называемые агрегатными состояниями). Фазовый переход (фазовое превращение), в широком смысле – переход вещества из одной фазы в другую при изменении внешних условий (Т, Р, магнитных и электрических полей и т.д.); в узком смысле – скачкообразное изменение физических свойств при непрерывном изменении внешних параметров. Будем далее рассматривать фазовые переходы в узком смысле. Различают фазовые переходы I рода и II рода. Фазовый переход I рода – широко распространенное в природе явление. К ним относятся: испарение и конденсация, плавление и затвердевание, сублимация или возгонка (переход вещества из кристаллического состояния непосредственно, без плавления, в газообразное, например, сухой лед) и конденсация в твердую фазу и др. Фазовые переходы I рода сопровождаются выделением или поглощением теплоты (теплоты фазового перехода q), при этом скачком изменяются плотность, концентрация компонентов, молярный объем и т.д. Фазовый переход II рода не сопровождается выделением или поглощением теплоты, плотность изменяется непрерывно, а скачком изменяется, например, молярная теплоемкость, удельная электрическая проводимость, вязкость и др. Примерами фазовых переходов II рода могут служить переход магнитного вещества из ферромагнитного состояния (m>> 1) в парамагнитное (m» 1) при нагреве до определенной температуры, называемой точкой Кюри; переход некоторых металлов и сплавов при низких температурах из нормального состояния в сверхпроводящее и др.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.62.99 (0.007 с.) |


 , в результате имеем P=RT/(V-b) – a/
, в результате имеем P=RT/(V-b) – a/  или
или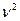 a/
a/  Левая, круто спадающая часть ее АВ соответствует жидкому состоянию, правая пологая часть FG – газообразному. Переход из жидкого состояния в газообразное и обратно при обычных условиях происходит не вдоль участка ВСDEF, а вдоль изобары BF, которая одновременно является и реальной изотермой. Такой изобаре-изотерме BF соответствуют двухфазные состояния вещества – жидкость + газ (пар). Чем ближе к точке В, тем больше жидкости, и чем ближе к точке F –тем больше в системе пара (газа). Заметим, что пар и газ – это одно и то же. Когда говорят о паре какой-либо жидкости, то этим желают подчеркнуть, что речь идет о газе, полученном испарением этой жидкости.
Левая, круто спадающая часть ее АВ соответствует жидкому состоянию, правая пологая часть FG – газообразному. Переход из жидкого состояния в газообразное и обратно при обычных условиях происходит не вдоль участка ВСDEF, а вдоль изобары BF, которая одновременно является и реальной изотермой. Такой изобаре-изотерме BF соответствуют двухфазные состояния вещества – жидкость + газ (пар). Чем ближе к точке В, тем больше жидкости, и чем ближе к точке F –тем больше в системе пара (газа). Заметим, что пар и газ – это одно и то же. Когда говорят о паре какой-либо жидкости, то этим желают подчеркнуть, что речь идет о газе, полученном испарением этой жидкости. С ростом температуры область горбов и впадин на изотерме ВдВ уменьшается и при температуре ТКР – критической температуре – превращается в точку перегиба К с горизонтальной касательной. В точке К исчезают различия между жидкой и газообразной фазой (однородная среда).
С ростом температуры область горбов и впадин на изотерме ВдВ уменьшается и при температуре ТКР – критической температуре – превращается в точку перегиба К с горизонтальной касательной. В точке К исчезают различия между жидкой и газообразной фазой (однородная среда).


