
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ І. Основні поняття теорії ігор таСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЗМІСТ ВСТУП РОЗДІЛ І. ОСНОВНІ ПОНЯТТЯ ТЕОРІЇ ІГОР ТА ВИКОРИСТАННЯ МЕТОДІВ ТЕОРІЇ ІГОР ПРИ ПРИЙНЯТТІ УПРАВЛІНСЬКИХ РІШЕНЬ 1.1. Основні поняття теорії ігор. 1.2. Класифікація ігор 1.3. Матричні ігри двох осіб 1.4. Гра зі змішаними стратегіями 1.5. Геометрична інтерпретація гри 2´2 1.6. Зведення гри до задачі лінійного програмування РОЗДІЛ ІІ. ПРАВИЛА ТА КРИТЕРІЇ ПРИЙНЯТТЯ РІШЕНЬ В УМОВАХ НЕВИЗНАЧЕНОСТІ 2.1. Особливості застосування методів теорії ігор при прийнятті управлінських рішень 2.2. Критерії при прийнятті рішень в умовах невизначеності 2.3. Прийняття рішень в умовах конфлікту 2.4. Прийняття рішень в умовах ризику ВИСНОВКИ СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ВСТУП «…Гра – не філософія і не релігія, Г. Гессе «Гра в бісер» Актуальність теми. У будь-якому сучасному підручнику з економіки можна побачити багатовимірні матриці та дерева рішень, які використовуються для пояснення стратегічної взаємодії між різними економічними суб’єктами. Неважливо, чи йде мова про книгу з макроекономіки, адресовану розробникам економічної політики, або про статтю про держанні фінанси. Теорія ігор привела до революції в методології економічної науки за останні двадцять років. У 1971 р. теорія ігор була ледве відома в наукових колах і ставлення до неї було скептичним. У 40-х і на початку 50-х років великі надії покладалися на те, що розробка цієї теорії забезпечить усі соціальні науки єдиною теоретичною базою, яка розгалужуватиметься на наукові напрями. Теорію ігор створив видатний математик Джон фон Нейман. Спочатку багато зусиль пішло на розробку ігор із нульовою сумою, в яких виграш одного гравця виходить за рахунок іншого. Спочатку теорія ігор іноді неадекватно використовувалася для пояснення динамічної стратегічної взаємодії. Особливо часто ігнорувалася послідовність або хронологія взаємодій, тому мало уваги приділялося внутрішній узгодженості взаємодій між гравцями. За останні двадцять років швидко розповсюджувалося використання теорії ігор в економіці, політиці, соціології та інших пов'язаних із ними сферах. Теорія ігор зараз краще пояснює основи економічного розвитку і спирається на більш послідовні концепції рішень, тому економісти почали використовувати її переважно для вирішення деяких спірних питань. Основну задачу теорії ігор можна сформулювати так: визначити, яку стратегію має застосувати розумний гравець у конфлікті з розумним противником, аби гарантувати кожному з них виграш при чому так, що відхилення будь-якого з гравців від оптимальної стратегії може тільки зменшити його виграш. В більшості випадків для прийняття управлінських рішень використовується неповна і неточна інформація, яка і утворює ситуацію невизначеності. Для обґрунтування рішень в умовах невизначеності використовують методи теорії ігор. Центральне місце в теорії ігор займають парні ігри з нульовою сумою, тобто ігри, в яких: Ø приймають участь тільки дві сторони; Ø одна сторона виграє рівно стільки, скільки програє інша. Мета написання курсової роботи полягає у з’ясуванні та засвоєнні основ теорії ігор, аналізі процесу прийняття рішень в умовах невизначеності. Відповідно до вищенаведеної мети поставлено такі завдання: 1) визначити сутність поняття „теорія ігор”; 2) з’ясувати шляхи застосування теорії ігор в прийнятті управлінських рішень; 3) визначити основні критерії при прийнятті управлінських рішень в умовах невизначеності. При написанні курсової роботи виділено два розділи. У першому розділі на основі огляду літературних джерел розкрито сутність поняття „теорія ігор”, проаналізовано основні види ігор та методи їх розв’язування. У другому розділі проаналізовано основні методи та механізми аналізу процесу прийняття рішення в умовах невизначеності, ризику та конфлікту. Інформаційною основою дослідження стали монографії, статті, посібники, підручники, інформаційні ресурси мережі Інтернет.
РОЗДІЛ І. ОСНОВНІ ПОНЯТТЯ ТЕОРІЇ ІГОР ТА ВИКОРИСТАННЯ МЕТОДІВ ТЕОРІЇ ІГОР ПРИ ПРИЙНЯТТІ УПРАВЛІНСЬКИХ РІШЕНЬ Основні поняття теорії ігор Теорія ігор – це розділ дослідження операцій, що займаються теорією математичних моделей прийняття оптимальних рішень в умовах конфлікту[11; с. 271]. При цьому математичні моделі, що застосовуються, є достатньо спрощеними та ідеалізованими схемами реальних явищ. Теорія ігор досліджує питання поведінки і виробляє оптимальні правила (стратегії) поведінки для кожного з учасників конфліктної ситуації[11; с. 272].Розв'язання суперечностей за допомогою теорії ігор можливе лише після проведення математичного моделювання ситуацій у вигляді гри. Теорія ігор вперше була систематично викладена Джоном фон Нейманом і Моргенштерном та оприлюднена лише 1944 року в монографії «Теорія ігор і економічної поведінки», хоча окремі результати були опубліковані ще в 20-х роках [20; с. 81]. Нейман і Моргенштерн написали оригінальну книгу, яка містила переважно економічні приклади, оскільки економічні задачі простіше за інші описати за допомогою чисел. Під час другої світової війни і одразу після неї теорією ігор серйозно зацікавились військові, які одразу побачили в ній математичний апарат для дослідження стратегічних проблем і підготовки рішень. Потім головна увага знову була звернута до економічних проблем. Нині сфера застосування теорії ігор значно розширилась. Так, у соціальних науках апарат теорії ігор застосовується у психології для аналізу торгових угод та переговорів, а також для вивчення принципів формування коаліцій тощо. За умов ринкової економіки все частіше мають місце конфліктні ситуації, коли два або більше колективів (індивідуумів) мають протилежні цілі та інтереси, причому результат дії кожної із сторін залежить і від дії супротивника [16; с. 422-423]. Класичним прикладом конфліктної ситуації в економіці є відношення продавець – покупець (монополія – монопсонія). Складніші ситуації виникають, коли в суперечці інтересів беруть участь об’єднання чи коаліції. Часто однією із сторін конфлікту є природні процеси чи явища, наприклад, погода, тобто маємо гру людини з природою. Погодними умовами людина практично не може керувати, але вона має змогу пристосовуватися до її постійних змін. Безліч подібних ситуацій можна зустріти і в інших сферах людської діяльності: біології, психології, політології тощо. Теорія ігор – це математичний апарат, що розглядає конфліктні ситуації, а також ситуації спільних дій кількох учасників. Завдання теорії ігор полягає у розробленні рекомендацій щодо раціональної поведінки учасників гри [16; с. 423]. Існує дуже багато різних ігор. Прикладом «гри» в буквальному розумінні цього слова, передусім, є спортивна, карточна гра, шахи тощо. Від реальної конфліктної ситуації гра відрізняється не лише спрощеною формою, а також наявністю певних правил, за якими мають діяти її учасники. Дослідження таких формалізованих ігор звичайно не може дати чітких рекомендацій для реальних умов, проте є найзручнішим об’єктом для вивчення конфліктних ситуацій і оцінки можливих рішень з різних поглядів. Розраховані на основі ігрових моделей оптимальні плани не визначають єдине правильне рішення за складних реальних умов, проте слугують математично обґрунтованою підставою для прийняття таких рішень. Метою теорії ігор є вироблення рекомендацій щодо розумної поведінки учасників конфлікту [2; с.175]. Теорія ігор як математична дисципліна в її сучасному стані займається нормативним вивченням ігор.
Рис. 1.1. Основні задачі теорії ігор Джерело: [11; с.273].
Нехай необхідно прийняти рішення про випуск на ринок певного товару. Обсяг попиту на цей товар може бути точно відомим, або може бути відомий лише статистичний розподіл можливих значень попиту, або можуть бути відомими лише межі значень, яких може набувати величина попиту, але ніяких ймовірнісних суджень про його майбутні значення немає. Останній випадок – ситуація невизначеності. Така невизначеність може виникнути, коли попит залежить від метеорологічних умов або в умовах ринку, від діяльності конкурента тощо. Наведені приклади можуть бути зведені до гри. У теорії ігор розроблена система власних понять [20; с.82-83]: Ø математична модель конфліктної ситуації називається грою; Ø сторони у конфлікті називаються гравцями (можуть бути як окремі особи, так і колективи людей, які мають спільні цілі: конкуруючі підприємства, спортивні команди); Ø результат гри називається виграшем або нічиєю; Ø правилами гри називається перелік прав і обов’язків гравців; Ø розрізняють поняття „ гра ” і „ партія гри ”. В даному випадку під грою розуміють сукупність правил, яка визначає поведінку гравців, а під партією гри – реалізацію гри певним конкретним чином від початку до кінця (наприклад, партія гри в шахи); Ø ходом називається вибір гравцем однієї з передбачених правилами гри дій. Ходи бувають особисті і випадкові. Особистий хід – це свідомий вибір гравця. Випадковий хід – вибір дії, що не залежить від його волі. Залежно від кількості можливих ходів у грі, ігри поділяються на: а) скінченні – ті, які передбачають скінчене число ходів; б) нескінченні – ті, які передбачають нескінчене число ходів. Ø стратегією гравця називається сукупність правил, що визначають вибір варіанта дій у кожному особистому ході; Ø оптимальною стратегією гравця називається така стратегія, що забезпечує йому максимальний виграш; Ø завдання теорії ігор полягає у виявленні оптимальної стратегії; Ø ігри, що складаються тільки з випадкових ходів, називаються азартними, ними теорія ігор не займається. Її мета – оптимізація поведінки гравця у грі, де поряд з випадковими є особисті ходи. Такі ігри називаються стратегічними; Ø гра називається грою з нульовою сумою, якщо сума виграшів всіх гравців дорівнює нулю, тобто кожен виграє за рахунок іншого; Ø гра називається парною, якщо в неї грають два гравці. Парна гра з нульовою сумою називається антагоністичною. Теорія таких ігор найбільш розвинена. Крім того, такі ігри моделюють великий клас реальних конфліктів. В подальшому розглядатимемо саме антагоністичні ігри. Основне припущення, на підставі якого знаходять оптимальні рішення в теорії ігор, полягає в тому, що супротивник такий же розумний, як і сам гравець [21; с.12].
Класифікація ігор Різні види ігор можна класифікувати, ґрунтуючись на тому або іншому принципі: за кількістю стратегій, властивостями функцій виграшу, за можливістю попередніх переговорів і взаємодії між гравцями у процесі гри. Класифікація ігор реалізується за певною множиною класифікаційних ознак, а саме: кількість гравців, кількість стратегій, характер взаємин між гравцями, характер виграшів, вигляд функції виграшів, момент вибору ходу, кількість ходів, стан інформації (рис.1.2).
Рис. 1.2. Класифікація ігор Джерело: [11; с. 275-276]. Кількість гравців. Залежно від кількості гравців розрізняють ігри: одного гравця, двох гравців, п гравців. Ігри одного гравця (наприклад пасьянс) не представляють інтересу і не розглядаються в теорії ігор. Ігри двох гравців – найбільш поширені, їх дослідженню присвячено багато робіт, і досягнуті найбільші успіхи як в теорії, так і в практичній діяльності. Ігри трьох і більше гравців менш досліджені через те, що виникають принципові труднощі при одержанні рішень. Труднощі рішення ігор підвищуються зі збільшенням кількості гравців [18; с. 10]. Кількість стратегій: скінчені та нескінчені. Якщо в грі кожен з гравців має скінчену множину можливих стратегій, то гра є скінченою, якщо ж хоча б один з гравців має безмежну множину стратегій, то гра є нескінченою. Зі зростанням кількості стратегій зростає складність розв'язання ігор.
Характер виграшів. За цією ознакою ігри поділяються на ігри з нульовою сумою та ігри з ненульовою сумою. В грі з нульовою сумою сума виграшів всіх гравців в кожній партії рівна нулю, тобто в цій грі загальний капітал всіх гравців не змінюється, а перерозподіляється між гравцями в залежності від результатів гри. Гра двох гравців з нульовою сумою називається антагоністичною, оскільки цілі гравців в ній прямо протилежні: виграні одного гравця досягається за рахунок програшу іншого. Прикладом гри з ненульовою сумою є торговельні взаємовідносини між країнами – в результаті застосування своїх стратегій всі країни можуть бути в виграші. Будь-яка гра, в якій необхідно виплачувати вступний внесок за право участі в ній, є грою з ненульовою сумою; у виграші завжди особа, що отримала внесок. В лотереї організатор завжди має виграш, а учасники гри отримують сумарний виграш менший, ніж внесли. Вигляд функції виграшів. За цією ознакою ігри поділяються на матричні, біматричні, неперервні, опуклі, сепарабельні, типу дуелей та ін. Матрична гра – це скінчена гра двох осіб, в якій виграш першого гравця задається елементами матриці і дорівнює програшу другого гравця. Матричні ігри розв'язуються за допомогою методів лінійного програмування. В біматричних іграх виграш кожного з гравців задається окремою матрицею, і ці ігри є складнішими для розв'язування. Якщо функція виграшу в грі може бути представлена у вигляді суми функцій одного аргумента, то така гра є сепарабельною (може бути розділеною). Дуель – це гра, що характеризується моментом вибору ходу та ймовірностями отримання виграшу в залежності від часу, що пройшов від моменту початку гри до моменту вибору. Наприклад: кожна фірма вкладає капітал в певний момент часу, чим раніше буде здійснене вкладення, тим менша вірогідність оволодіти ринком, однак і при занадто пізньому вкладенні ринок збуту буде втрачено [11; с. 276]. Кількість ходів. За цією ознакою ігри поділяються на однокрокові та багатокрокові. Однокрокові ігри завершуються після того, як кожен з гравців зробить по одному крокові. Матрична гра є однокроковою. Багатокрокові ігри своєю чергою поділяються на позиційні, стохастичні та диференційні. Позиційні ігри полягають у тому, що кожен їїгравців робить декілька ходів послідовно в часі, і виграші визначаються в залежності від результату гри. Якщо ж у грі робляться ходи, що приводять до вибору певних позицій, причому існує певна вірогідність повертання на попередню позицію, то така гра називається стохастичною. Якщо ходи робляться неперервно і умови їх проведення описуються диференційними рівняннями (гра типу «хижак-жертва»), то така гра називається диференційною [18; с. 11]. Стан інформації. За цією ознакою розглядаються ігри з повною та неповною інформацією. Якщо на кожному ході гри кожному з гравців відомо, які вибори були зроблені гравцями раніше, то гра є з повною інформацією (шахи, шашки). Якщо ж у грі не все відомо про попередні вибори, то гра буде з неповною інформацією [11; с. 277].
Матричні ігри двох осіб Найчастіше розглядається гра з двома гравцями, в якій виграш однієї сторони дорівнює програшу іншої, а сума виграшів обох сторін дорівнює нулю, що в теорії ігор називають грою двох осіб з нульовою сумою [4; с. 213]. Подібна ситуація є типовою у практичній діяльності менеджерів, маркетологів, спеціалістів рекламних служб, які щоденно приймають рішення за умов гострої конкуренції, неповноти інформації тощо. Основною метою розв’язування задач цього класу є розроблення рекомендацій щодо вибору оптимальних стратегій конфліктуючих сторін на основі застосування методичних підходів теорії ігор. Отже, маємо два гравці А і В (гра двох осіб з нульовою сумою). Кожний гравець вибирає одну із можливих стратегій: позначимо стратегії гравця А – Результати (плата) за всіма можливими варіантами гри задаються спеціальними функціями, які залежать від стратегій гравців, як правило, у вигляді платіжної матриці. Нехай,
Оскільки гра з нульовою сумою, то Тоді в разі, якщо Отже, мета гравця А – максимізувати величину
де рядки відповідають стратегіям Аі, а стовпці – стратегіям Bj. Матриця А називається платіжною, а також матрицею гри. Елемент цієї матриці aij – це виграш гравця А, якщо він вибрав стратегію Ai, а гравець В – стратегію Bj [16; с. 425]. Із багатьох критеріїв, які пропонуються теорією ігор для вибирання раціональних варіантів рішень, найпоширенішим є песимістичний критерій мінімаксу та максиміну. Суть цього критерію у наступному. Нехай гравець А вибрав стратегію Ai, тоді у найгіршому разі він отримає виграш, що дорівнює min aij, тобто навіть тоді, якщо гравець В і знав би стратегію гравця А. Передбачаючи таку можливість, гравець А має вибрати таку стратегію, щоб максимізувати свій мінімальний виграш, тобто [20; с. 83]
Така стратегія гравця А позначається Гравець В, який програє суми у розмірі елементів платіжної матриці, навпаки має вибрати стратегію, що мінімізує його максимально можливий програш за всіма варіантами дій гравця А. Стратегія гравця В позначається через
Оптимальний розв’язок цієї задачі досягається тоді, коли жодній стороні невигідно змінювати вибрану стратегію, оскільки її супротивник може у відповідь вибрати іншу стратегію, яка забезпечить йому кращий результат. Якщо
тобто, якщо Приклад 1.1. Фірма виготовляє устаткування для хімічної промисловості. Експертами виробничого відділу фірми розглядаються три конструкторські варіанти устаткування: А -1, А -2, А -3. Для спрощення припустимо, що за технічними характеристиками ці три типи майже ідентичні, однак залежно від зовнішнього вигляду та зручності використання кожен тип може мати три модифікації: М -1, М -2, М -3 залежно від закупленої технології виробництва. Собівартість виготовлення устаткування наведена в табл. 1.1 [16; с. 426-427]: : Таблиця 1.1 В УМОВАХ НЕВИЗНАЧЕНОСТІ Таблиця значень цільової функції F (x, z)
Тут рядок відповідає значенню x, а стовпець – значенням z. Так значення F (200, 150) знаходиться на перетині третього рядка (x = 200) і другого стовпця (z = 150). При цьому
F (200, 150)=24´min{200;150}–10´(200 – min{200;150})=3600 – 500=3100.
Оцінимо ефективність довільній стратегії х. Оцінювати будемо за критеріями «очікуване значення» і «очікуване значення-дисперсія». За критерієм «очікуване значення» маємо
=
+
Аналогічно отримуємо
Отже, за критерієм «очікуване значення» кращою є стратегія х*= 200. Знайдемо тепер рішення за критерієм
W 9(100)= W 7(100) –
W 9(150)= W 7(150) – =3260-680=2580;
W9(200)= W 7(200) – – »3695 – 1447 = 2348;
Аналогічно отримуємо
W 9(250)» 2023; W9(300)»1437.
Отже, в цьому випадку кращою виявилася більш обережна стратегія закупівлі – 150 булочок щодня. Критерій граничного рівня. Цей критерій відповідає не поняттю оптимальності, а прийнятного способу дії. Даний критерій застосовується, коли важко оцінити виграш (програш) при тій чи іншій стратегії ОПР [3; с. 256-257]. Розглянемо приклад. Приклад 2.4. Припустимо, що величина попиту z за одиницю часу на товар є випадковою величиною з безперервною функцією щільності розподілу Визначити втрати від дефіциту товару в повному обсязі дуже важко, тому ОПР може прийняти рішення виходячи з критерію граничного рівня, домагаючись, щоб величина очікуваного дефіциту не перевищувала А1 одиниць, а величина очікуваних надлишків не перевищувала А2 одиниць. Математично це можна записати в даному прикладі наступним чином. Нехай I – визначений рівень запасів, тоді
При довільному виборі А1 і А2 зазначені умови можуть виявитися суперечливими. У цьому випадку необхідно збільшити одне або обидва обмеження, щоб забезпечити існування рішення. Наведений приклад не єдина ситуація, коли використовується цей критерій. Критерій граничного рівня має сенс застосовуватися, коли в момент рішення немає повного уявлення про всю множину альтернатив або, коли виникають труднощі для ОПР у визначенні усієї множини альтернатив і обчисленню на цій множині значень критерію операції, які перевершують втрати від неточного рішення. Нехай, наприклад, власник підприємства сфери послуг, що може працювати з різною швидкістю обслуговування (пральня, ресторан, перукарня), розглядає питання про швидкість обслуговування. Швидке обслуговування, задовольняючи інтереси клієнтів, може виявитися невигідним для власника, тому що вимагає додаткових витрат на нове обладнання і кількість обслуговуючого персоналу. Повільне обслуговування вимагає менших витрат, але може призвести до втрати клієнтів, які не бажають довго чекати. Нехай в даній ситуації можна задати або визначити з експерименту розподіл ймовірностей потоку клієнтів і часу їх обслуговування. В силу багаторазового проведення операції з надання послуг представляється прийнятним визначення оптимального рівня швидкості обслуговування виходячи з мінімізації загальних очікуваних втрат за одиницю часу. Загальні втрати складаються з витрат на надання послуг і втрати очікуваного прибутку в разі відмови клієнта чекати обслуговування. Обидві складові втрат залежать від рівня швидкості обслуговування, при цьому, чим більше значення першої, тим менше значення другої і навпаки. Однак розглянутий критерій практично непридатний через труднощі оцінювання прийнятного часу очікування для різних клієнтів. ВИСНОВКИ В результаті проведеного дослідження були зроблені наступні висновки: Теорія ігор – це розділ прикладної математики, який вивчає моделі і методи прийняття оптимальних рішень в умовах конфлікту. Під конфліктом розуміється така ситуація, в якій зіштовхуються інтереси двох або більше сторін, що переслідують різні (найчастіше суперечні) цілі. При цьому кожне рішення має прийматися в розрахунку на розумного противника, який намагається зашкодити другому учаснику гри досягти успіху. З метою дослідження конфліктної ситуації будують її формалізовану спрощену модель. Аби побудувати таку модель необхідно чітко описати конфлікт, тобто: Ø уточнити кількість учасників (учасники або сторони конфлікту називаються гравцями); Ø вказати на всі можливі способи (правила) дій для гравців, які називаються стратегіями гравців; Ø розрахувати, якими будуть результати гри, якщо кожний гравець вибере певну стратегію (тобто з’ясувати виграші або програші гравців). Чисті стратегії – це пара стратегій (одна – для першого гравця, а друга – для другого гравця), які перехрещуються в сідловій точці. Сідлова точка в цьому випадку і визначає ціну гри. Ігри, які не мають сідлової точки, на практиці зустрічаються частіше. Доведено, що і у цьому випадку рішення завжди є, але воно знаходиться в межах змішаних стратегій. Знайти рішення гри без сідлової точки означає визначення такої стратегії, яка передбачає використання кількох чистих стратегій. В іграх із сідловою точкою відхилення одного гравця від своєї оптимальної стратегії зменшує його виграш (в найкращому випадку виграш залишається незмінним).
В іграх, які не мають сідлової точки, ситуація інша. Відходячи від своєї оптимальної стратегії гравець має можливість отримати виграш більший за нижню ціну гри. Але така спроба пов’язана з ризиком: якщо другий гравець вгадає, яку стратегію застосував перший, тоді він також відступить від своєї мінімаксної стратегії. В результаті виграш першого гравця буде меншим за нижню ціну гри. Єдина можливість завадити противнику вгадати, яка стратегія використовується – це застосувати декілька чистих стратегій. Звідси з’являється поняття «змішана стратегія». Задачі теорії ігор належать до задач прийняття рішень за умов невизначеності та ризику. Невизначеність результатів гри зумовлена кількома чинниками. По-перше, як правило, кількість можливих варіантів розвитку подій дуже велика, тому передбачити результат гри неможливо. Простою ілюстрацією такого твердження є гра в шахи. Із-за безлічі можливих комбінацій знайти оптимальний розв’язок такої гри неможливо. По-друге, значний вплив на хід та результати гри мають випадкові чинники, дію яких передбачити неможливо, наприклад, у рулетці. По-третє, джерелом невизначеності є брак інформації щодо дій противника. Крім того, невизначеність певною мірою може стосуватися також і мети, якої прагне досягти суб’єкт. Не завжди таку мету можна виразити однозначно, а тим більше одним показником. Отже, уможливлюючи розв’язування задач за умов невизначеності, навіть якщо неможливо знайти точний оптимальний розв’язок, методи теорії ігор являють собою допоміжний матеріал, який дає змогу в складній ситуації оцінити кожен з можливих варіантів розвитку подій, а отже, прийняти виважене рішення. СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 1. Блюмин С. Л. Модели и методы принятия решений в условиях неопределенности / С. Л. Блюмин, И. А. Шуйкова – Липецк: ЛЭГИ, 2001. – 138с. 2. Вентцель Е. С. Исследование операций / Е. С. Вентцель – М.: Советское радио, 1972. – 209 с. 3. Вітлінський В.В. Ризикологія в економіці та підприємництві: Монографія / В.В. Вітлінський, Г.І. Великоіваненко– К.: КНЕУ, 2004. – 480 с. 4. Вітлінський В. В. Математичне програмування: Навч. посібник для самост. вивч. дисц. / В. В. Вітлінський, С. І. Наконечний, Т. О. Терищенко. – К.: КНЕУ, 2001. – 248 с. 5. Вітлінський В.В., Шарапов О.Д. Теорія інтелектуальних систем прийняття рішень // Моделювання та інформаційні системи в економіці: Зб. наук. праць. – Київ: КНЕУ, 2008. – Вип. 78. – с. 58-69. 6. Воробьев Н. Н. Теория игр для экономистов-кибернетиков / Н. Н.° Воробьев. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 272 с. 7. Дерлоу Д. Ключові управлінські рішення: Технологія прийняття рішень: [Посібник] / Пер. з англ. Р. А. Семків, Р. Л. Ткачук. – К.: Наук. думка, 2001. – 242 с.: іл., табл. 8. Дж. фон Нейман, О. Моргенштейн. Теория игр и экономическое поведение. Перев. с англ. под ред. и с доб. Н. Н. Воробьева. Главная редакция физико-математической литературы, изд-ва «Наука», 1970. – 708 с. 9. Дюбин Г. Н. Введение в прикладную теорию игр / Г. Н. Дюбин, В. Г.° Суздаль – М.: Наука. Главная редакция физико-математической литературы, 1981. – 332 с. 10. Зайченко Ю. П. Дослідження операцій. Підручник. Сьоме видання перероблене та доповнене / Ю. П. Зайченко. – К.: Видавничий Дім «Слово», 2006. – 816 с. 11. Катренко А. В. Дослідження операцій: Підручник / Анатолій Васильович Катренко. – 2-ге вид. стереотипне. – Львів: «Магнолія Плюс», 2005. – 549 с. 12. Клименко С. М. Обґрунтування господарських рішень та оцінка ризиків: Навч. Посібник / С. М. Клименко, О. С. Дуброва. – К.: КНЕУ, 2005. – 252 с. 13. Крушевский А. В. Теория игр. – Киев, Издательское обьединение «Вища школа», 1977 – 216 с. 14. Ларичев О.И. Теория и методы принятия решений, а также хроника событий в Волшебных странах: Учебник. изд. второе, перераб. и доп.– М.: Логос, 2002. – 392 с.: ил. 15. Литвак Б.Г. Разработка управленческих решений: Учебник. – 3-е изд., испр. – М.: Дело, 2002. – 392 с. 16. Наконечний С. І. Математичне програмування: Навч. посіб. / С. І.° Наконечний, С. С. Савіна. – К.: КНЕУ, 2003. – 452 с. 17. Оуэн Г. Теория игр: Пер. с анг. – М.: Мир, 1971. – 230 с. 18. Петросян Л. А. и др. Теория игр: Учеб. пособие для ун-тов: / Л. А.° Петросян, Н. А. Зенкевич, Е. А. Семина. – М.: Высш. шк. Книжный дом «Университет», 1998. – 304 с.: ил. 19. Печерский С. Л. Теория игр для экономистов. Вводный курс. Учебное пособие / С. Л. Печерский, А. А. Беляева– СПб.: Изд-во Европ. Ун-та в С.-Петербурге, 2001. – 342 с. 20. Половян Н. С. Методи прийняття управлінських рішень: [навчальний посібник] / Н.С. Половян; Міністерство освіти і науки України, Донецький національний університет. – Донецьк: Норд-Прес, ДонНУ, 2010. – 236 с. 21. Протасов И. Д. Теория игр и исследование операцій: Учебное пособие / И. Д. Протасов. – М.: Гелиос АР
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 968; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.15.91 (0.013 с.) |
























 Характер взаємин. За цією ознакою ігри поділяються на безкоаліційні, коаліційні та кооперативні. Безкоаліційними є ігри, в яких заборонені угоди між гравцями та утворення коаліцій (наприклад, чемпіонат світу з футболу). Коаліційними називаються ігри, в яких гравці можуть утворювати коаліції (військові ігри, економічні ситуації, пов'язані з оволодінням певними ринками збуту). Кооперативними є ігри, в яких коаліції відомі наперед та залишаються незмінними протягом гри.
Характер взаємин. За цією ознакою ігри поділяються на безкоаліційні, коаліційні та кооперативні. Безкоаліційними є ігри, в яких заборонені угоди між гравцями та утворення коаліцій (наприклад, чемпіонат світу з футболу). Коаліційними називаються ігри, в яких гравці можуть утворювати коаліції (військові ігри, економічні ситуації, пов'язані з оволодінням певними ринками збуту). Кооперативними є ігри, в яких коаліції відомі наперед та залишаються незмінними протягом гри.
 стратегії гравця В –
стратегії гравця В – 
 .
.
 – виграш гравця А;
– виграш гравця А;

 то
то 
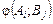 , а гравця В – мінімізувати її. Нехай
, а гравця В – мінімізувати її. Нехай 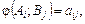 тобто маємо матрицю А:
тобто маємо матрицю А:
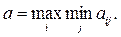 (1.1)
(1.1)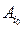 і має назву максимінної, а величина гарантованого виграшу цього гравця називається нижньою ціною гри.
і має назву максимінної, а величина гарантованого виграшу цього гравця називається нижньою ціною гри. і називається мінімаксною, а величина його програшу – верхньою ціною гри, тобто [20; с. 84]
і називається мінімаксною, а величина його програшу – верхньою ціною гри, тобто [20; с. 84] (1.2)
(1.2) , (1.3)
, (1.3) то гра називається цілком визначеною [20; с. 84]. В такому разі виграш гравця А (програш гравця В) називається ціною гри і дорівнює елементу матриці
то гра називається цілком визначеною [20; с. 84]. В такому разі виграш гравця А (програш гравця В) називається ціною гри і дорівнює елементу матриці  . Цілком визначені ігри називаються іграми з сідловою точкою, а елемент платіжної матриці, значення якого дорівнює виграшу гравця А (програшу гравця В) і є сідловою точкою. В цій ситуації оптимальним рішенням гри для обох сторін є вибір лише однієї з можливих, так званих чистих стратегій – максимінної для гравця А та мінімаксної для гравця В, тобто якщо один із гравців притримується оптимальної стратегії, то для другого відхилення від його оптимальної стратегії не може бути вигідним.
. Цілком визначені ігри називаються іграми з сідловою точкою, а елемент платіжної матриці, значення якого дорівнює виграшу гравця А (програшу гравця В) і є сідловою точкою. В цій ситуації оптимальним рішенням гри для обох сторін є вибір лише однієї з можливих, так званих чистих стратегій – максимінної для гравця А та мінімаксної для гравця В, тобто якщо один із гравців притримується оптимальної стратегії, то для другого відхилення від його оптимальної стратегії не може бути вигідним.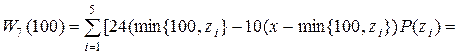
 ;
;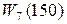 =1900
=1900 
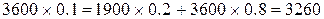 ;
;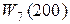 =(
=(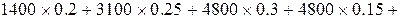
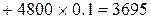 ;
;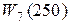 =3495;
=3495; 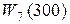 =3040.
=3040. (див. (15)) при K = 1
(див. (15)) при K = 1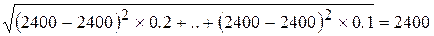 ;
;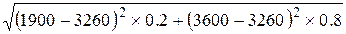 =
=
 (z), тобто d(
(z), тобто d( (z)) =
(z)) = 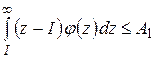 ,
, 



