
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прийняття рішень в умовах конфліктуСодержание книги
Поиск на нашем сайте
Сформулюємо завдання прийняття рішень у вигляді завдання оптимізації [23; с. 83-84]
На відміну від попередніх випадків, коли параметром z управляла «Природа», тут ми припускаємо, що параметром z управляє «розумний» противник, що переслідує власні цілі. Ці цілі виражаються за допомогою завдання прийняття рішення (ПР), аналогічно (2.20):
Отже, нехай два суб'єкти А і Б, що володіють можливістю вибору, відповідно, елементів Розбіжність між функціоналами Легко уявити собі ситуацію, коли не два, а
Обидві особи, які приймають рішення (ОПР), або обидва «гравця», мають можливість вибору х і z відповідно. Далі для визначеності будемо вважати, що Далі ми всюди будемо вважати себе гравцем А і проводити міркування з позицій його інтересів. У зв'язку з тим, що результат нашого вибору рішення залежить від вибору гравця Б, необхідно зробити якісь припущення про його можливу поведінку в процесі виконання завдання. Правомірність подібних припущень (Гіпотез) прямо залежить від характеру інформованості сторін про поведінку іншої сторони. При грі з «думаючим» противником, який переслідує в процесі прийняття своїх рішень цілком визначені цілі, розумно вдаватися до інших гіпотез, для кращого відображення суті такого завдання. Будемо розрізняти такі основні гіпотези (випадки) [23; с. 84-86]. Гіпотеза 1. Кожен із суб'єктів А і Б не має інформації про вибір, зроблений другою стороною. Додаткові гіпотези про характер поведінки другого гравця відсутні. У цьому випадку можна поступати аналогічно рішенню задачі в умовах невизначеності. Це, по суті, той же випадок, і ми можемо скористатися відомим принципом найкращого гарантованого результату. Для суб'єкта А гарантована оцінка буде дорівнює
а для суб'єкта Б
Вирішуючи завдання максимізації (2.22), (2.23), ми знаходимо і вектори Приклад 2.2. Дамо графічну ілюстрацію застосування принципу гарантованого результату. Нехай
Будемо вважати, що
Позначимо
Таким чином, для обчислення одного значення функції
будь-яке
що досягається при
На рис. 2.1, а представлені лінії постійного рівня функціоналу J (x, z) на площині (х, z).
Рис. 2.1. Принцип гарантованого результату Джерело: [23; с. 86].
Згадаймо, що лінією рівня називається геометричне місце точок на площині, де На рис. 2.1б зображено залежність
При виборі значення Гіпотеза 2. Припускаємо, що суб'єкт Б слідує принципу максиміна і вибирає
Тоді ми можемо вибирати
де
де Гіпотеза 3. Тепер ми можемо припустити, що суб'єкт міркує точно так само, як і в попередньому випадку, тобто використовує не стратегію
Гіпотеза 4. Можливий інший вид гіпотез: ми за умовами гри знаємо перший хід суб'єкта Б (він зобов'язаний повідомити його нам). Тоді наша поведінка буде визначатися стратегією у вигляді функції
Умова (2.27) дозволяє для кожного фіксованого z визначити шукане значення Для цього випадку ми також можемо визначити гарантований результат
Таким чином, прийняття гіпотези 4 знову дозволяє поліпшити результат, отриманий за принципом максиміна гарантованого результату. Гіпотеза 5. Нехай Б знає наш перший хід. У цьому випадку природно припустити, що він буде дотримуватися стратегії
Прийняття цих припущень, тобто припущення про те, що ми повідомили свій хід суб'єкту Б, а також допущення про використання Б стратегії
Якщо максимум у співвідношенні (2.29) досягається не в одній точці
Загальним для всіх розглянутих випадків є припущення, що обидві сторони, що беруть участь в грі, не тільки точно знають свої цілі, але й повністю інформовані про цільові функції «супротивника» або партнера по грі. Для реальних конфліктних ситуацій це не завжди виконується. Набагато частіше ми не знаємо точно цілей наших партнерів, які в свою чергу, мають обмежену інформацію про наших наміри. Крім того, необхідно враховувати і можливу свідому дезінформацію, «блеф» з боку кожного з гравців. Та й гравців може бути не два, а більше.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.255.170 (0.006 с.) |

 (2.20)
(2.20) (2.21)
(2.21) , прагнуть до досягнення своїх цілей, представлених у вигляді (2.20), (2.11).
, прагнуть до досягнення своїх цілей, представлених у вигляді (2.20), (2.11). визначає ступінь антагонізму гравців. В окремому випадку може виявитися, що
визначає ступінь антагонізму гравців. В окремому випадку може виявитися, що  при будь-яких
при будь-яких  ; таку ситуацію, що виникає в грі двох суб'єктів, називають антагоністичною, строго конкурентною або грою з нульовою сумою
; таку ситуацію, що виникає в грі двох суб'єктів, називають антагоністичною, строго конкурентною або грою з нульовою сумою  [23; с. 83]. Найбільш типовий конфлікт, в якому інтереси гравців не співпадають, але і не строго протилежні.
[23; с. 83]. Найбільш типовий конфлікт, в якому інтереси гравців не співпадають, але і не строго протилежні. гравців максимізують свої виграші
гравців максимізують свої виграші  . В цьому випадку, наприклад, для першого гравця, що вибирає рішення
. В цьому випадку, наприклад, для першого гравця, що вибирає рішення  решта
решта  становитимуть фактор невизначеності
становитимуть фактор невизначеності  . Якщо
. Якщо  , то ми як і раніше говоримо про гру з нульовою сумою, хоча термін «антагоністична гра» тут уже непридатний. Далі ми будемо розглядати тільки ігри двох осіб. Отже, нехай дві сторони А і Б прагнуть до досягнення своїх цілей:
, то ми як і раніше говоримо про гру з нульовою сумою, хоча термін «антагоністична гра» тут уже непридатний. Далі ми будемо розглядати тільки ігри двох осіб. Отже, нехай дві сторони А і Б прагнуть до досягнення своїх цілей:

 т. е.
т. е.  (2.22)
(2.22) . (2.23)
. (2.23) які реалізують відповідні гарантовані оцінки.
які реалізують відповідні гарантовані оцінки. і потрібно мінімізувати
і потрібно мінімізувати  . У результаті ми маємо антагоністичну гру:
. У результаті ми маємо антагоністичну гру:

 є множини всіх дійсних чисел(Тут ми використовуємо очевидну обставину, що замість пошуку мінімуму функції
є множини всіх дійсних чисел(Тут ми використовуємо очевидну обставину, що замість пошуку мінімуму функції  можна шукати максимум функції
можна шукати максимум функції  . Для даного прикладу гарантована оцінка знаходиться з умови
. Для даного прикладу гарантована оцінка знаходиться з умови
 . (2.24)
. (2.24) при фіксованому
при фіксованому  необхідно вирішити задачу оптимізації (2.24). Отримаємо
необхідно вирішити задачу оптимізації (2.24). Отримаємо
 призводить до зменшення функції
призводить до зменшення функції  . Тепер знаходимо
. Тепер знаходимо
 . Таким чином, ми отримаємо
. Таким чином, ми отримаємо  і при цьому
і при цьому  . Це гарантований результат, бо при будь-якому
. Це гарантований результат, бо при будь-якому  ми будемо мати значення
ми будемо мати значення  не гірше (тобто не більше), ніж нуль, тобто при будь-якому
не гірше (тобто не більше), ніж нуль, тобто при будь-якому 

 . Міняючи постійну
. Міняючи постійну  , ми будемо отримувати різні лінії рівня. Якщо функція залежить більш ніж від двох перемінних, то слід говорити не про лінії рівня, а про поверхні рівня.
, ми будемо отримувати різні лінії рівня. Якщо функція залежить більш ніж від двох перемінних, то слід говорити не про лінії рівня, а про поверхні рівня. в тривимірному просторі, має характерний вигляд «сідла». Можна вважати, що відповідна поверхню «склеєна» з двох видів парабол:
в тривимірному просторі, має характерний вигляд «сідла». Можна вважати, що відповідна поверхню «склеєна» з двох видів парабол:
 ми при різних
ми при різних  .
. з умови (2.23):
з умови (2.23):
 згідно з правилом
згідно з правилом (2.25)
(2.25) – гарантує рішення другого гравця. Позначимо рішення завдання (2.25) через
– гарантує рішення другого гравця. Позначимо рішення завдання (2.25) через  . При цьому виявляється, що
. При цьому виявляється, що (2.26)
(2.26) – наша гарантована оцінка, отримувана за принципом максимина.
– наша гарантована оцінка, отримувана за принципом максимина.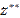 . Тому ми можемо це врахувати і вибирати оптимальне рішення з урахуванням вже цієї гіпотези:
. Тому ми можемо це врахувати і вибирати оптимальне рішення з урахуванням вже цієї гіпотези:
 Ми можемо її визначити в результаті рішення задачі оптимізації
Ми можемо її визначити в результаті рішення задачі оптимізації (2.27)
(2.27) .
.
 . Результат
. Результат  , знайденого відповідно до гіпотези 1. Саме, у всіх випадках будемо мати
, знайденого відповідно до гіпотези 1. Саме, у всіх випадках будемо мати (2.28)
(2.28) , яка будується в результаті рішення оптимізаційної задачі
, яка будується в результаті рішення оптимізаційної задачі (2.29)
(2.29)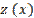 , дозволяє нам так впливати на вибір суб'єкта Б, щоб він у максимальному ступені відповідав нашим цілям. Саме, ми можемо вибирати х з умови
, дозволяє нам так впливати на вибір суб'єкта Б, щоб він у максимальному ступені відповідав нашим цілям. Саме, ми можемо вибирати х з умови
 , то наш гарантований результат
, то наш гарантований результат  визначається з умови:
визначається з умови:



