
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерії при прийнятті рішень в умовах невизначеностіСодержание книги
Поиск на нашем сайте
Розглянемо випадок, коли Z тобто немає випадкових факторів, і m = 1
f: X Тоді найбільш поширеними є наступні способи оцінки ефективності стратегій. Принцип найкращого гарантованого результату (критерій Вальда). Передбачається, що для кожної стратегії х
Оцінку W1(х) (2.5) називають ще оцінкою крайнього песимізму. Таким чином, у розглянутому випадку величина W1(x) оцінює «виграш» ОПР знизу, тобто, вибравши стратегію х
Застосування принципу найкращого гарантованого результату обґрунтовано, коли вибір невизначеного фактора у У випадку, коли ОПР прагне мінімізувати величину f(x, y), замість оцінки W1(x) (2.5) застосовується аналогічна оцінка
Відповідно
Якщо ОПР не протистоїть розумний противник, застосування принципу найкращого гарантованого результату може здатися дуже «песимістичним». У цих випадках говорять про «ігри з природою». Неконтрольовані фактори вибирає «природа», ґрунтуючись на своїх, невідомих ОПР, цілях. Найбільш відомими в даній ситуації є критерії Лапласа, Севіджа і Гурвіца [20; с. 90]. Критерій Лапласа. Цей критерій ґрунтується на принципі недостатнього обґрунтування. Оскільки розподіл ймовірностей на невизначених факторах невідомо, то приймаємо, що цей розподіл є розподілом рівномірного закону. Критерій Лапласа оцінює стратегію х
де pi – імовірність того, що неконтрольований фактор прийме значення y i. При цьому pi=1/i.
Перша формула застосовується у випадку безперервної випадкової величини y. Друга формула для скінченної множини Y ={ y 1 ,…,ym }. Приклад 2.1. Підприємство має визначити рівень пропозиції послуг так, щоб задовольнити потребу клієнтів протягом майбутніх свят. Точне число клієнтів невідомо, але воно може приймати одне з чотирьох значень: y1 = 200, y2 = 250, y3 = 300, y4 = 350. Для кожного з цих можливих значень існує найкращий рівень пропозиції (x1,..., x4) з точки зору мінімізації витрат. Відхилення від цих рівнів призводять до додаткових витрат або через перевищення пропозиції над попитом, або із-за неповного задоволення попиту (додаткові витрати через необхідність термінових закупівель, втрачений прибуток) [23; с. 77]. Значення витрат в залежності від рівня послуг і можливого числа клієнтів задані у вигляді таблиці. За критерієм Лапласа події y1, y2, y3, y4 рівноймовірні. Отже, для будь-якого iÎ
У цьому випадку очікувані витрати при різних рівнях пропозиції послуг складає відповідно: M{x1} = 0.25×5+0.25×10+0.25×18+0.25×25=14.5; M{x2} = 11.5; M{x3} = 18.0; M{x4} = 21.5. Найкращим рівнем пропозиції послуг відповідно до критерію Лапласа буде x2. Критерій Севіджа. Розглянемо наступний приклад. Нехай множини X ={ x 1, x2 } та Y ={ y 1, y 2} складаються тільки з двох елементів. Цільова функція є функцією витрат ОС, яка задана таблицею [2; с. 200].
Застосування критерію найкращого гарантованого результату дає як рішення стратегію x2. Проте, якщо ОПР застосує стратегію x1, то при гіршому для нього варіанті y = y1 витрати зростуть в порівнянні з гарантованим результатом на 1%, а при сприятливому варіанті витрати складуть тільки 0,9% від гарантованих витрат, тобто зменшаться на 99.1%. Врахувати подібні ситуації і реалізувати вибір стратегії, який дає можливо невеликий програш, але й можливо істотний виграш у порівнянні зі стратегією гарантованого результату, дозволяє критерій Севіджа. Нехай цільова функція f (x, y) є функція виграшу ОПР. Отже, ОПР прагне максимізувати цільову функцію. Складемо функцію жалю [22; с. 150-151]:
Величина
Функцію
У випадку, коли в моделі операції задана функція втрат (програшу), функція жалю буде мати вигляд
яка знову висловлює «співчуття» ОПР про те, що вона для цього невизначеного фактора y
Далі, оптимальна за даним критерієм стратегія х0 шукається з критерію найкращого гарантованого результату для
Функція жалю і у випадку функції виграшу f (формула (2.11)) і у випадку функції втрат f (формула (2.14)) виражає величину втрат ОПР від незастосування кращої стратегії. Тому критерій найкращого гарантованого результату в обох випадках є мінімаксний:
Складемо матрицю жалю для наведеного на початку пункту прикладу. Так як функція f (i, j) в даному прикладі є функція втрат, то
Функцію S=
Тепер з критерію найкращого гарантованого результату для матриці S отримуємо, що оптимальною буде стратегія х1. Розглянемо приклад 2.1. Так як в цьому прикладі задана функція втрат, то функція жалю

Для знаходження оптимальної за критерієм Севіджа стратегії ОПР знайдемо по матриці жалю S стратегію х0, що задовольняє принцип найкращого гарантованого результату. Для цього потрібно знайти максимальний елемент у кожному рядку матриці S. Позначимо його b1, b2, b3, b4, відповідно. Потім необхідно знайти найменше з чисел bi . Тоді номер i*: b i*= min{ b j} – визначить оптимальну стратегію. У прикладі 2.1 b1 = 10, b2 = 8, b3 = 16, b4 = 25. Відповідно, i0 = 2, тому що b 2=min{ b 1; b 2; b 3; b 4}. Отже, стратегія х2 є оптимальною за критерієм Севіджа в даному прикладі. Ця відповідь збігається з відповіддю, отриманими за критерієм Лапласа. Таким чином, для наведеної в прикладі 2.1 функції втрат оптимальною і за критерієм Лапласа, і за критерієм Севіджа є стратегія х2. Однак з наведеного прикладу не варто робити висновок, що такий збіг буде завжди виконуватися. Можна навести приклад, коли ці два критерії будуть вважати оптимальними різні стратегії. Критерій Гурвіца. Для визначення наступного критерію нам знадобиться поняття опуклої комбінації [23; с. 78]. Означення 10. Число с називається опуклою комбінацією чисел a і b, якщо існує число
C =
Зазначимо, що множина таких чисел утворює відрізок [a; b]. Критерій Гурвіца є опуклою комбінацією критеріїв крайнього песимізму W1 (x, у) і крайнього оптимізму:
Тут ми вважаємо, що задана функція виграшу f (x, y). Критерій крайнього оптимізму припускає, що невизначений фактор y
Оптимальною в цьому випадку вважається стратегія х 0
W 5(х 0)=
Для функції втрат
W 6 (x)=
Оптимальною при цьому вважається стратегія х 0 W 6 (x 0)= Параметр α називається показником оптимізму: при α = 1 критерій Гурвіца перетворюється на критерій крайнього оптимізму, при α = 0 – в критерій крайнього песимізму. Вибір параметра здійснюється ОС, виходячи з його поглядів на дану операцію, тобто є суб'єктивним. Знайдемо рішення задачі з прикладу 2.1 за критерієм Гурвіца у разі α = 0.2. Відповідно маємо: W 6(x 1) = [0.2min{5; 10; 18; 25} + mах0.8{5; 10; 18; 25}] = 0.2´5 + 0.8´25 = 21, W 6(x 2) = [0.2´7 + 0.8´23] =19.8, W 6(x 3) = [0.2´12 + 0.8´21] = 19.2, W 6 (х 4) = [0.2´15 + 0.8´30] = 27. Аналізуючи залежність вибору оптимальної стратегії від значення α, отримаємо [23; с. 79-80]:
Ø Ø Ø Ø Ø
Таким чином, залежно від обраної величини оптимізму ОС може отримати різні відповіді про оптимальність стратегії.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.102 (0.008 с.) |

 Y
Y 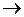 R (2.4)
R (2.4)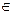 X ОПР буде реалізовуватися найгірший для ОПР невизначений фактор у
X ОПР буде реалізовуватися найгірший для ОПР невизначений фактор у 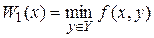 (2.5)
(2.5)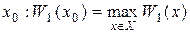 . (2.6)
. (2.6)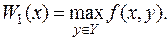 (2.7)
(2.7)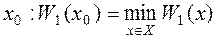 . (2.8)
. (2.8)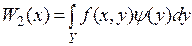 ,
, 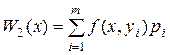 (2.9)
(2.9)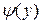 – функція щільності розподілу ймовірностей рівномірного закону;
– функція щільності розподілу ймовірностей рівномірного закону;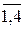 ймовірність того, що відбудеться подія yi дорівнює 0.25.
ймовірність того, що відбудеться подія yi дорівнює 0.25. (2.10)
(2.10)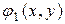 висловлює «співчуття» ОПР в тому, що вона для цього невизначеного фактора y вибрала стратегію x, а не кращу стратегію
висловлює «співчуття» ОПР в тому, що вона для цього невизначеного фактора y вибрала стратегію x, а не кращу стратегію 
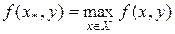 . (2.11)
. (2.11)
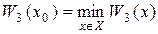 . (2.12)
. (2.12)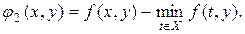 (2.13)
(2.13) :
: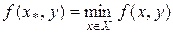 . (2.14)
. (2.14)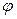 2(х, у):
2(х, у):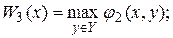


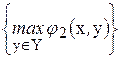 (2.15)
(2.15)
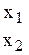

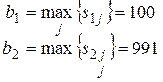
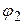 (i, j) обчислюється за формулою (2.14).
(i, j) обчислюється за формулою (2.14).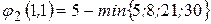 =5-5=0,
=5-5=0, 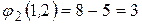 ,
, 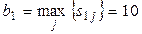
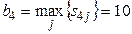

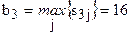

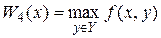 . (2.17)
. (2.17)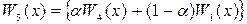 =
= 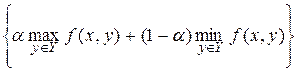 (2.18)
(2.18) W 5(x).
W 5(x). (х, у) критерій Гурвіца задається рівністю:
(х, у) критерій Гурвіца задається рівністю: . (2.19)
. (2.19)


